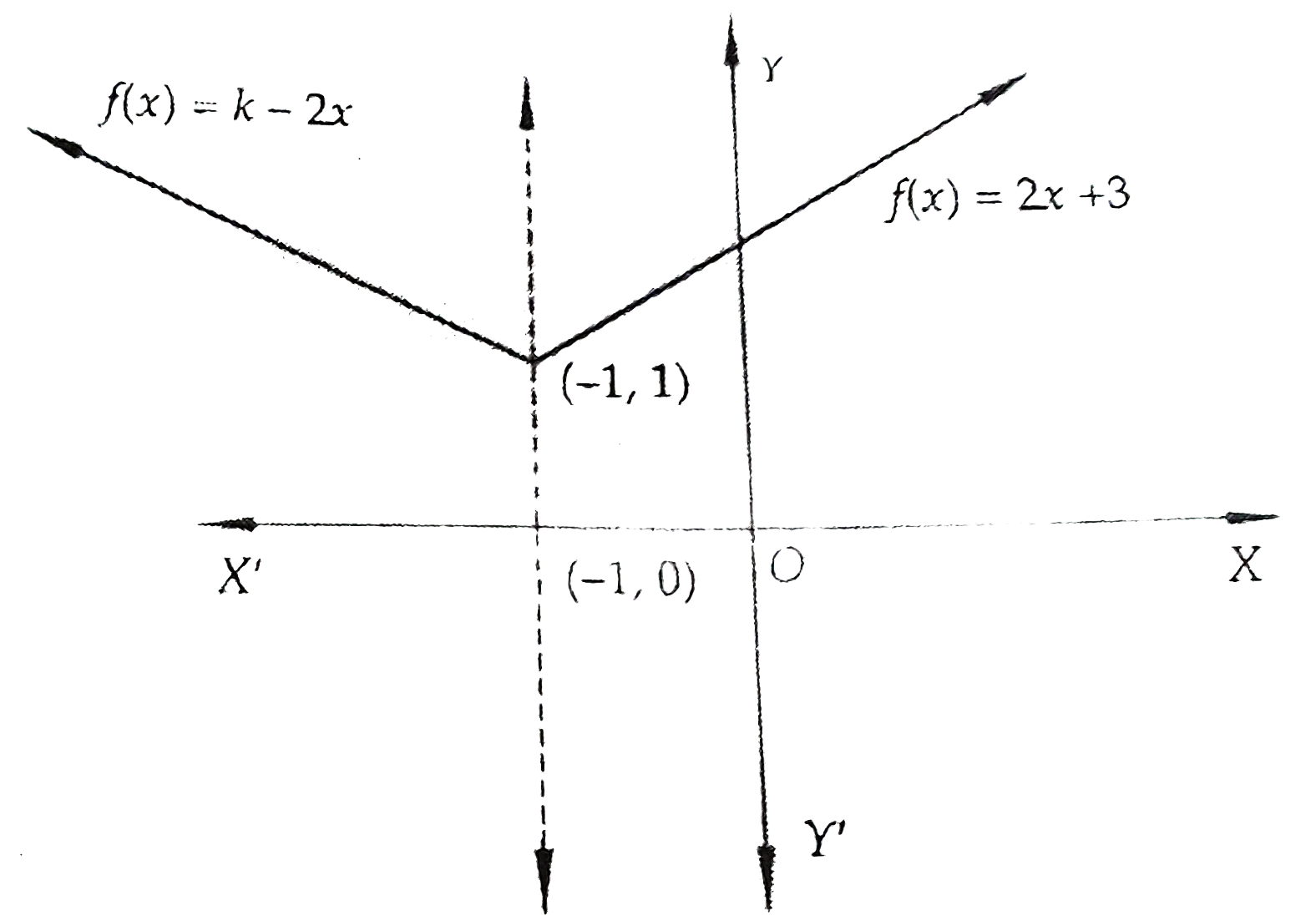
Let f:R to R be defined by f(x)={{:(2k-2x",",ifxle-1),(2x+3",",iffxg

Let $f (x) = {\begin{matrix} | x - 1 | + a & if x \leq 1 2 x + 3 & if x > 1 \end{matrix}$ . If f(x) has a local minimum at x=1, then
A $a > 5$
B $0 < a \leq 5$
C $a \leq 5$
D $a = 5$
Let $f (x) = {\begin{matrix} | x - 1 | + a, & x \leq 1 2 x + 3, & x > 1 \end{matrix}$ . If f(x) has local minimum at x=1 and $a \geq 5$ then the value of a is
A5
B6
C $11 / 2$
D $15 / 2$
Let $f : R \to R$ be defined by f(x)=3x-4. Then, $f^{- 1}$ (x) is
A $\frac{x + 4}{3}$
B $\frac{x}{3} - 4$
C $3 x + 4$
Dnone of these

Let $f : R \to R$ be defined by
$f (x) = {\begin{matrix} 2 k - 2 x, & if x \leq - 1 2 x + 3, & \Leftrightarrow x > - 1 \end{matrix}$
If f has a local minimum at x=-1, then a possible value of k is