The function $f (x) = 2 | x | + | x + 2 | = | | x | 2 | - 2 | x | ∣$ has a local minimum or a local maximum at $x =$ $- 2$ (b) $- \frac{2}{3}$ (c) 2 (d) $\frac{2}{3}$

A

$- 2 and - \frac{2}{3}$

B

(b)-2 and 0

C

$- \frac{2}{3} and 2$

D

$2 and - 2$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

We have ,
f(x)=2|x|+|x-2|-||x+2|-2|x|
$\Rightarrow$
$f (x) = ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ \begin{matrix} - 2 x - (x + 2) - | x - 2 | = - 2 x - x - 2 + x - 2 = - 2 x - 4, x < - 2 - 2 x + x + 2 - | x + 2 + 2 x | = - 2 x + x + 2 + 3 x + 2 = 2 x + 4, - 2 \leq x < - \frac{2}{3} - 2 x + x + 2 - | x + 2 + 2 x | = - 2 x + x + 2 - 3 x - 2 = - 4 x, - \frac{2}{3} < x < 0 2 x + x + 2 - | x + 2 - 2 x | = 2 x + x + 2 - (2 - x) = 4 x, 0 \leq x \leq 2 2 x + x + 2 - | x + 2 - 2 x | = 2 x + x + 2 - x = 2 x + 4, x > 2 \end{matrix}$
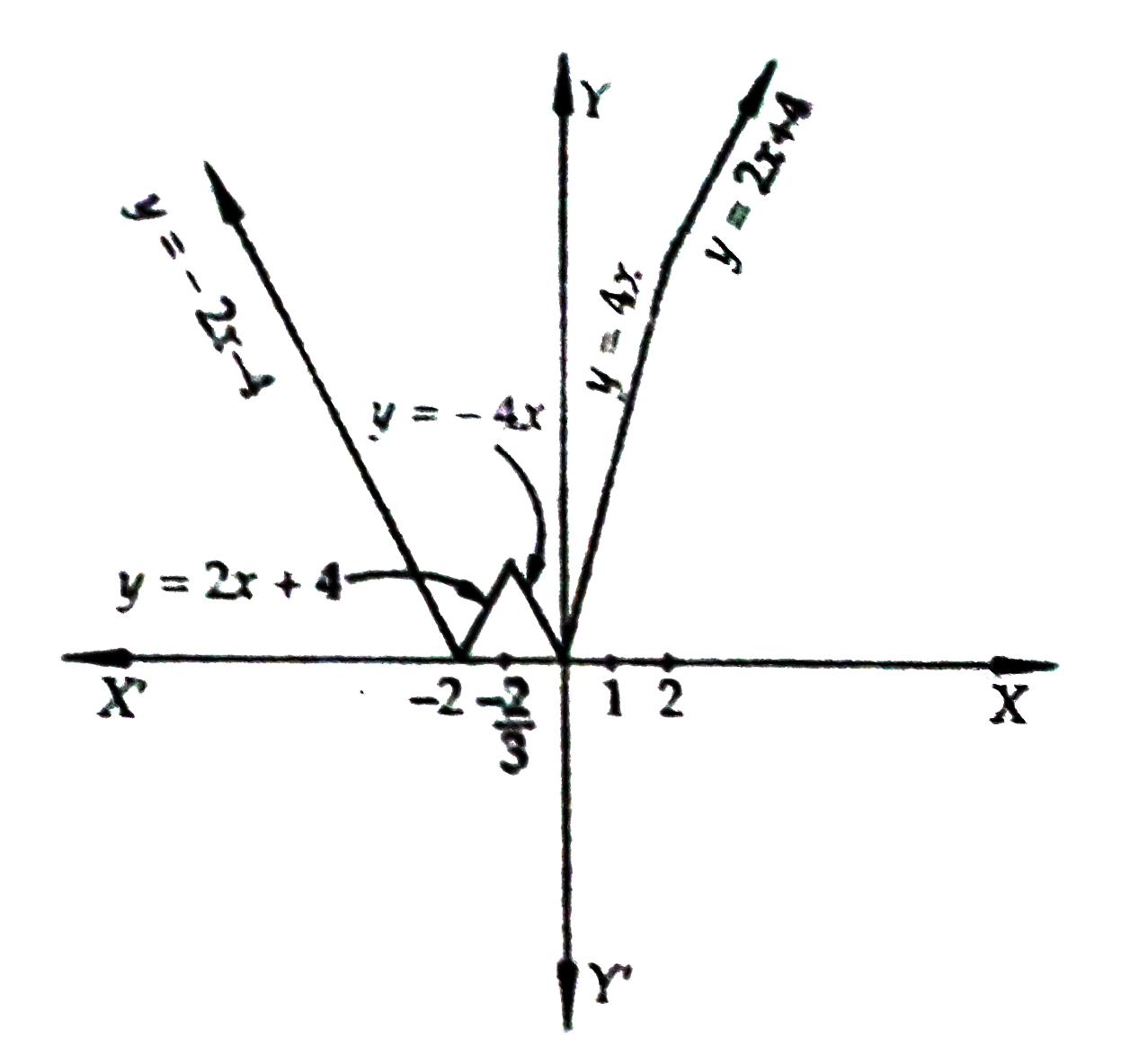
The graph of f(x) is shown in the following figure.
Clearly,x=-2 ,0 are points of local minima and $x = - \frac{2}{3}$ is a points of local maximum .

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

The function f(x)=2|x|+|x+2|-||x+2|-2|x|| has a local minimum or a local maximum at x equal to:
A $- 2$
B $\frac{- 2}{3}$
C2
D $\frac{2}{3}$
The function f(x)=2|x|+|x+2|-||x+2|-2|x|| has a local minimum or a local maximum at x equal to:
A $- 2$
B $- \frac{2}{3}$
C $2$
D $\frac{2}{3}$
The function $f (x) = \frac{2}{x} + \frac{x}{2}$ has a local minimum at x =
A $- 2$
B0
C1
D2

OBJECTIVE RD SHARMA-MAXIMA AND MINIMA -Section I - Solved Mcqs

Home
Ask Doubt
Profile