If z complex number satisfying |z−1|=1, then which of the following is correct
A
arg(z−1)=2arg(z)
B
2arg(z)=23arg(z2−z)
C
arg(z−1)=2arg(z+1)
D
argz=2arg(z+1)
Video Solution
Text Solution
The correct Answer is:A
Clearly, |z−1|=1 represents a circle with center at (1,0) and radius 1. Let P(z) be any point on it. Then,
arg(z−1)=∠XCP=θ (say)
∴arg(z)=∠XOP=θ2
Hence, arg(z-1) = 2arg(z)
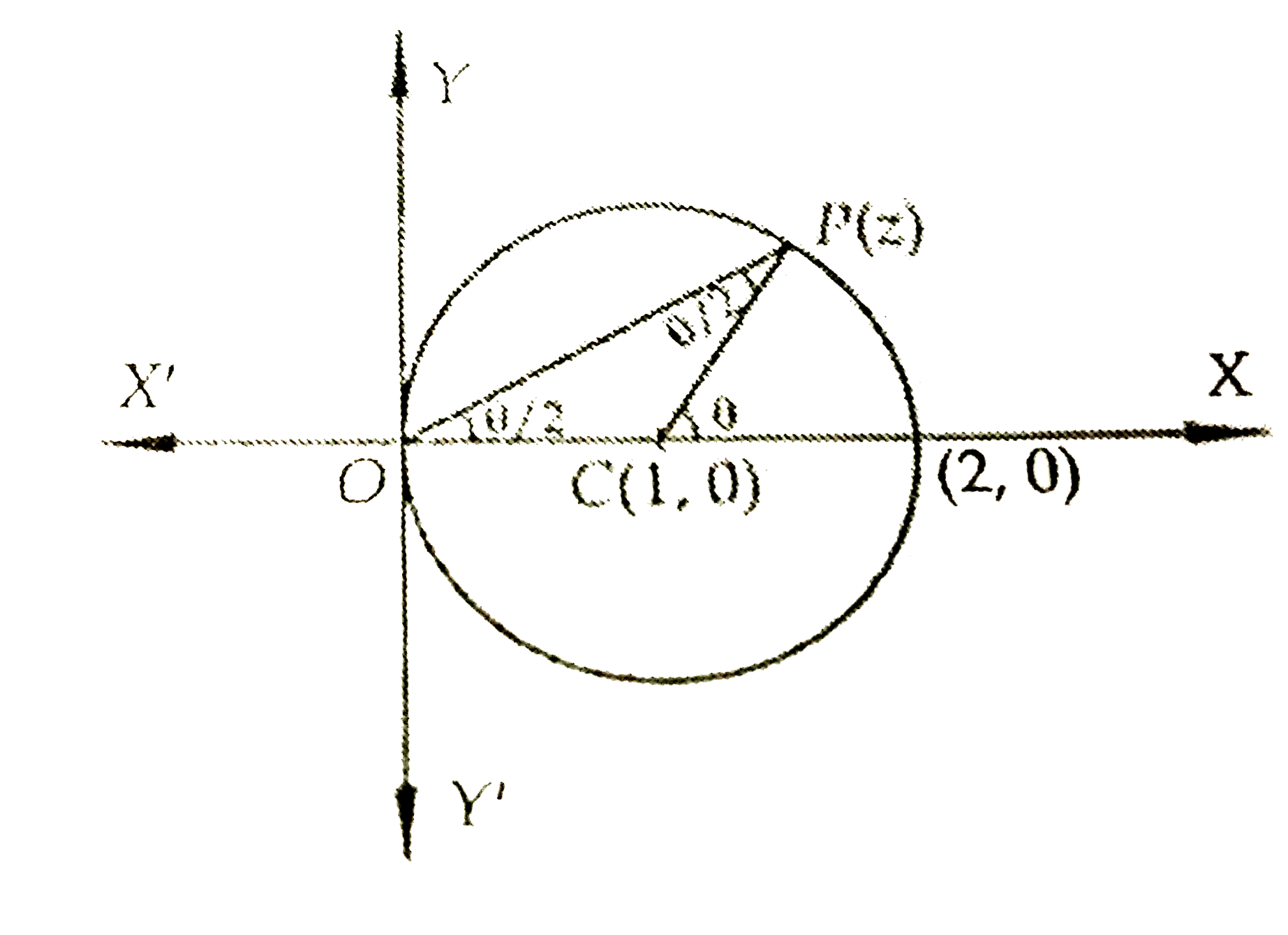
|
Topper's Solved these Questions
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Section II - Assertion Reason Type
15 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Exercise
131 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
59 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Chapter Test
55 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise
86 Videos
Similar Questions
Knowledge Check
Let s be the set of all complex numbers Z satisfying ∣∣z2+z+1∣∣=1. Then which of the following statements is/are TRUE?
A∣∣∣z+12∣∣∣≤12fora∣∣z∈SB|Z|≤2for allz∈SC∣∣∣z+12∣∣∣≥12for allz∈SDThe set S has exactly four elements.Let z1,z2 and z3 be three distinct complex numbers satisfying |z1|=|z2|=|z3|=1. Which of the following is/are true ?
AIf arg(z1z2)=π2 then arg (z−z1z−z2)>π4 where | z| gt 1B|z1z2+z2z3+z3z1|=|z1+z2+z3|Clim((z1+z2)(z2+z3)(z3+z1)z1.z2.z3)=0DIf |z1−z2|=√2|z1−z3|=√2|z2−z3|, then Re (z3−z1z3−z2) = 0Let z1,z2 and z3 be three distinct complex numbers , satisfying |z1|=|z2|=|z3|=1. Which of the following is/are true :
AIf arg(z1z2)=π2 then arg (z−z1z−z2)>π4 where |z| gt 1B|z1z2+z2z3+z3z1|=|z1+z2+z3|Clm((z1+z2)(z2+z3)(z3+z1)z1.z2.z3)=0DIf |z1−z2|=√2|z1−z3|=√2|z2−z3|, then Re(z3−z1z3−z2)=0
The complex number z satisfying z+|z|=1+zi then the value of |z|2 is
View SolutionIf z is a complex number satisfying the relation |z+1|=z+2(1+i), then z is
View SolutionIf z is a complex number satisfying ∣z+16∣=4|z+1| , then the minimum value of | z | is
View SolutionIf Re(z−1z+1)=0 where z=x+iy is a complex number, then which one of the following is correct ?
View SolutionLet z be a complex number satisfying |z+16|=4|z+1|. Then
View Solution
