Let OP.OQ=1 and let O,P and Q be three collinear points. If O and Q represent the complex numbers of origin and z respectively, then P represents

A

$\frac{1}{z}$

B

$¯ z$

C

$\frac{1}{¯ z}$

D

$- z$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Let P represent the complex number $z_{1}$
Let $z = r e^{i θ}$ . Then, OQ=r and arg(z)= $θ$
Since, O,P and Q are collinear points. Therefore,
$arg (z_{1}) = θ$ or $π + θ$
$\Rightarrow z_{1} = O P e^{i θ}$ or, $z_{1} = O p e^{i (π + θ)}$
$\Rightarrow z_{1} = \frac{O P . O Q}{O Q} e^{i θ}$ or, $z_{1} = (\frac{1}{O Q e^{- i θ}}$ or $z_{1} = - \frac{1}{O Q e^{- i θ}}$
$\Rightarrow z_{1} = \frac{1}{r e^{i θ}}$ or $z_{1} = - \frac{1}{r e^{i θ}}$
$\Rightarrow z = \frac{1}{¯ z}$ or $z_{1} = - \frac{1}{¯ z}$

|

Updated on:21/07/2023

Class 12 MATHS COMPLEX NUMBERS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Let $O$ , $A$ , $B$ be three collinear points such that $O A . O B = 1$ . If $O$ and $B$ represent the complex numbers $O$ and $z$ , then $A$ represents
A $\frac{1}{¯ z}$
B $\frac{1}{z}$
C $¯ z$
D $z^{2}$
Question 2 - Select One
In a given parallelogram, if the points $P_{1}$ and $P_{2}$ represent two complex numbers $z_{1}$ and $z_{2}$ , then the point $P_{3}$ represents the number
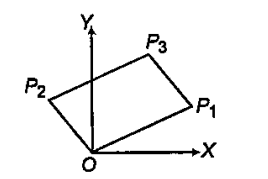A $z_{1} + z_{2}$
B $z_{1} - z_{2}$
C $z_{1} \times z_{2}$
D $z_{1} + z_{2}$
Question 3 - Select One
POQ is a straight line through the origin O,P and Q represent the complex numbers a+ib and c+id respectively and OP=OQ. Then, which one of the following is true?
A $| a + i b | = ∣ c +$
B $a + b = c + d$
C $arg (a + i b) = arg (c + id)$
Dnone of these

OBJECTIVE RD SHARMA-COMPLEX NUMBERS -Section I - Solved Mcqs

Home
Ask Doubt
Profile