Doubtnut Promotions Sticky

In arithmetic growth of length of organ against time is plotted, the curve is  

A

parabola

B

linear

C

sigmoid

D

rectangular

Text Solution
Verified by Experts

The correct Answer is:B

Doubtnut Promotions Banner
|
Updated on:21/07/2023
Class 11BIOLOGYPLANT GROWTH AND DEVELOPMENT

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    Arithmetic growth means

    Aout of two cells formed in each mitotic division only one cell continues to divide.
    Bout of two cells formed from one cell, two cells show continuous division.
    Cnone of the cells divide and add new cells.
    Dout of two cells formed both lose dividing ability.
  • Question 2 - Select One

    in arithmetic growth, following mitotic cell division, only one daughter cell continues to divide while the other differentiates and matures. The simplest expression of arithmetic growth is exemplified by a root elongating at a constant rate. On plotting the length of the organ against time, a linear curve is obtained, as seen in the graph. Mathemati cally, it is expressed as -
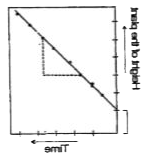    ocr_image

    ALt=L0+rt(Lt= Length at time 't' L0 = length at time 'zero' r = growth rate/ elongation per unit time).
    BLt=L0ert
    CLt=L0+rtorLt=L0ert
    DLt=2×L0
  • Question 3 - Select One

    Growth plotted against time gives a

    AParabolic curve
    BSigmoid curve
    CUpright line
    DHorizontal line.