A student did the experiment to find the equivalent resistance of two given resistors, R1 and R2 first when they are connected in series and next when they are connected in parallel. The two values of the equivalent resistance obtained by him were Rs and Rp respectively. Compare Rs and Rp.
In series, the equivalent resistance
Rs=R1+R2
In parallel, the equivalent resistance
1Rp=1R1+1R2
1Rp=R1+R2R1R2
Rp=R1R2R1+R2
Clearly, Rs>Rp.
Topper's Solved these Questions
- BOOK - VK GLOBAL PUBLICATIONCHAPTER - PRACTICAL BASED QUESTIONSEXERCISE - Experiment 64videos
PRACTICAL BASED QUESTIONS
- BOOK - VK GLOBAL PUBLICATIONCHAPTER - PRACTICAL BASED QUESTIONSEXERCISE - Experiment 74videos
PRACTICAL BASED QUESTIONS
- BOOK - VK GLOBAL PUBLICATIONCHAPTER - PRACTICAL BASED QUESTIONSEXERCISE - Experiment 46videos
PRACTICAL BASED QUESTIONS
- BOOK - VK GLOBAL PUBLICATIONCHAPTER - PERIODIC CLASSIFICATION OF ELEMENTS EXERCISE - PROFICIENCY EXERCISE (LONG ANSWER QUESTIONS)3videos
PERIODIC CLASSIFICATION OF ELEMENTS
- BOOK - VK GLOBAL PUBLICATIONCHAPTER - VALUE-BASED QUESTIONSEXERCISE - EXERCISE (CHAPTER-16) MANAGEMENT OF NATURAL RESOURCES9videos
VALUE-BASED QUESTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
Equivalent resistance R, of the parallel combination when two resistors Rand R, are connected in parallel is equal to
ARp=R1+R2R1R2BRp=R1R2R1−R2CRp=R1−R2R1+R2DRp=R1+R2R1+R2 - Question 2 - Select One
In order to determine the equivalent resistance of two resistors R1 and R2 connected in series, a student made this circuit for his experiment.
The only statement which is true for this circuit is that it gives :
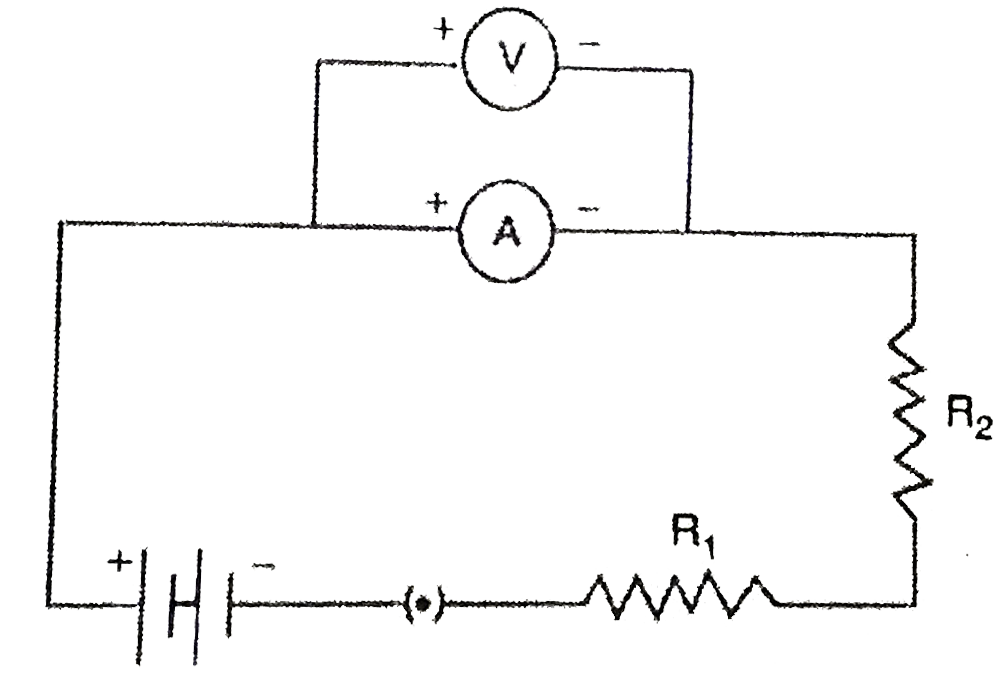 Aincorrect readings for current I as well as for potential difference VBcorrect reading for current I but incorrect reading for potential difference VCincorrect reading for current I but correct reading for potential difference VDcorrect readings for both current I and potential difference V.
Aincorrect readings for current I as well as for potential difference VBcorrect reading for current I but incorrect reading for potential difference VCincorrect reading for current I but correct reading for potential difference VDcorrect readings for both current I and potential difference V. - Question 3 - Select One
Assertion (A): Resistances connected in parallel has higher equivalent resistance.
Reason (R): RP=R1+R2+….+RnABoth (A) and (R) are true and (R) is the correct explanation of (A).BBoth (A) and (R) are true but (R) is not the correct explanation of (A).C(A) is true but (R) is false.D(A) is false and (R) is also false.
The resistance 4R,16R,64R....∞ are connected in series. Find their equivalent resistance.
View SolutionIn an experiment to find the equivalent resistance of a series combination of two resistors R1 and R2,a student uses the circuit shown here. Will the circuit give the correct reading for current I and voltage V ? Justify your answer.
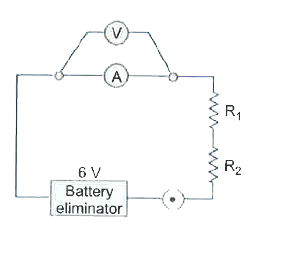 View Solution
View SolutionIf resistors of resistance R1 and R2 are connected in parallel,then resultant resistance is "
View SolutionAssertion (A): Resistances connected in parallel has higher equivalent resistance.
Reason (R): RP=R1+R2+…+RnView SolutionThe values of two resistors are R1=(6±0.3)kΩ and R2=(10±0.2)kΩ. The percentage error in the equivalent resistance when they are connected in parallel is
View Solution

