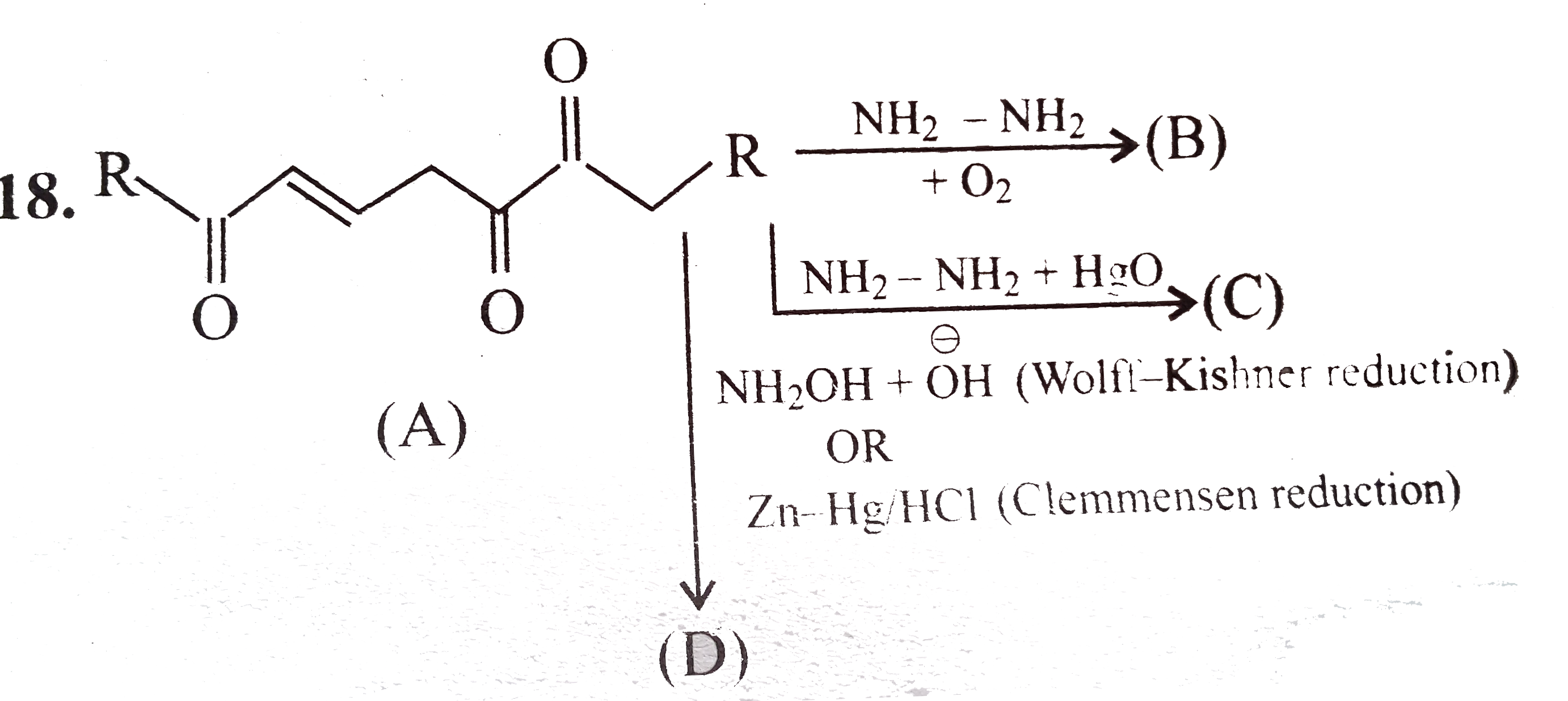
(B), (C), and (D), respectively, are
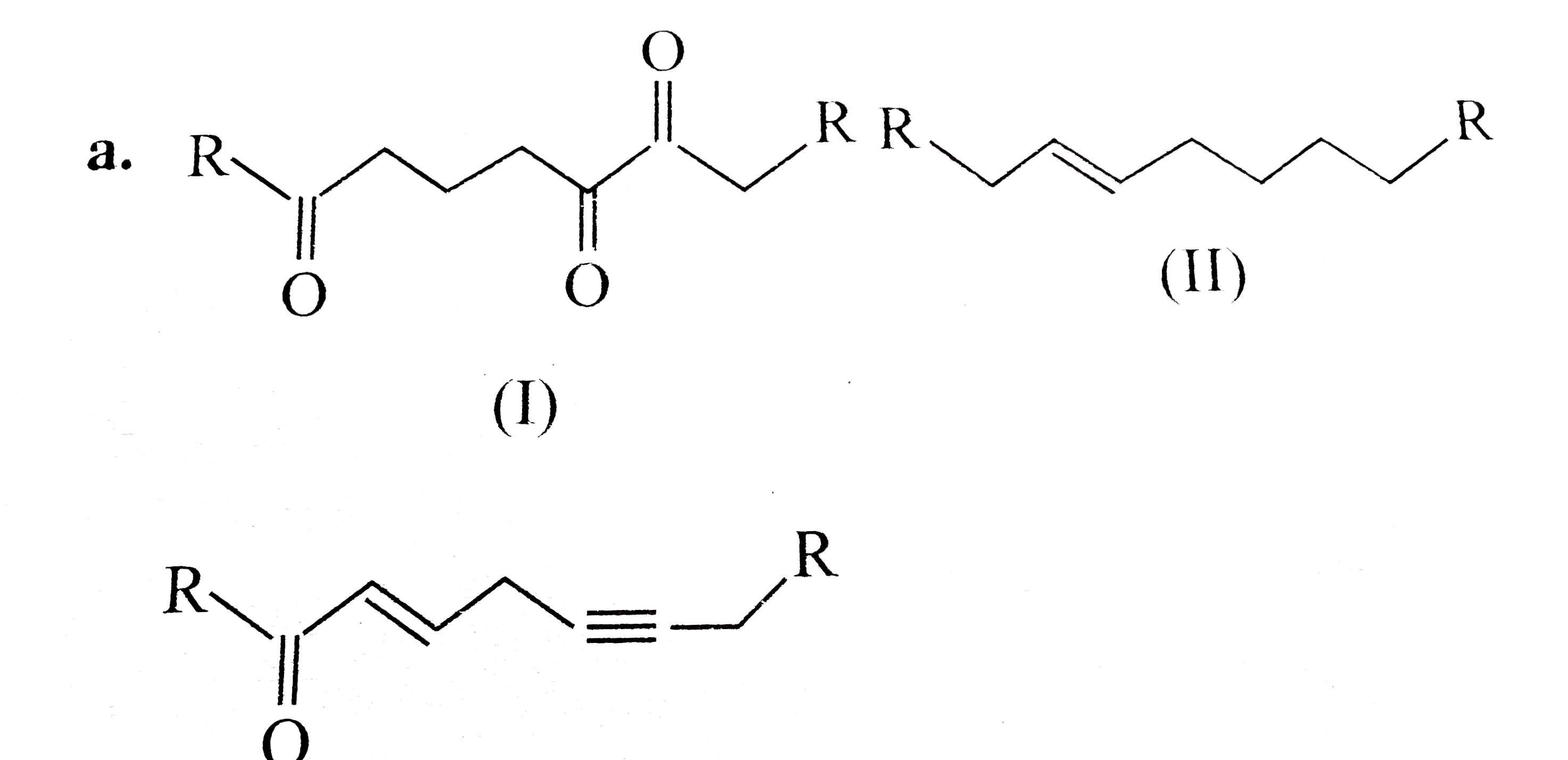
(b) (I), (III), (II)
(c) (III), (II), (I)
(d) (III), (I), (II)
The correct Answer is:B
Reagent converts double bond to single bond.
Reagent converts -diketone to . Reagent Wolf-Kishner of Clemmensen reduction converts 
group to group.
So the answer is (b).
Topper's Solved these Questions
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ALKYNESEXERCISE - Exercises (Archives - Single Correct Answer Type)6videos
ALKYNES
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ALKYNESEXERCISE - Exercises (Archives - Fill in the Blanks Type)3videos
ALKYNES
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ALKYNESEXERCISE - Exercises (Multiple Correct Answers Type)25videos
ALKYNES
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ALKENES AND ALKADIENESEXERCISE - Single correct Answer14videos
ALKENES AND ALKADIENES
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - APPENDIX - INORGANIC VOLUME 1EXERCISE - chapter-7 Single correct answer1videos
APPENDIX - INORGANIC VOLUME 1
Similar Questions
The compounds (B), (C ), (D), respectively are:View SolutionChoose the correct option for label (A), (B), (c ) and (D) respectively in given diagram.
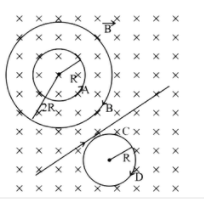
View SolutionFour particles A, B, and C and D of masses mA,mB,mBandmD respectively, follow the paths shown in the figure, in a uniform magnetic field. Each particle moving with same speed. QA,QB,QCandQD are the specific charge of particles A, B, C and D respectively (assume that the motion of each particle is in the same plane perpendicular to the magnetic field).
View SolutionIf →a ,→b ,→c ,→d are the position vector of point A,B,C and D , respectively referred to the same origin O such that no three of these point are collinear and →a + →c = →b + →d , than prove that quadrilateral ABCD is a parallelogram.
View SolutionIf →a ,→b ,→c ,→d are the position vector of point A,B,C and D , respectively referred to the same origin O such that no three of these point are collinear and →a + →c = →b + →d , than prove that quadrilateral ABCD is a parallelogram.
View SolutionIf →a,→b,→c,→d are the position vectors of points A,B,CandD, respectively referred to the same origin O such that no three of these points are collinear and →a+→c=→b+→d, then prove that quadrilateral ABCD is a parallelogram.
View SolutionIn the balanced chemical reaction
IOө3+aIө+bHө→cH2O+dI2
a,b,c, and d, respectively, correspond toView SolutionIn the balanced chemical reaction
IOө3+alө+bHө→cH2O+dI2
a,b,c, and d, respectively, correspond toView SolutionIn the balanced chemical reaction
IOө3+aIө+bHө→cH2O+dI2
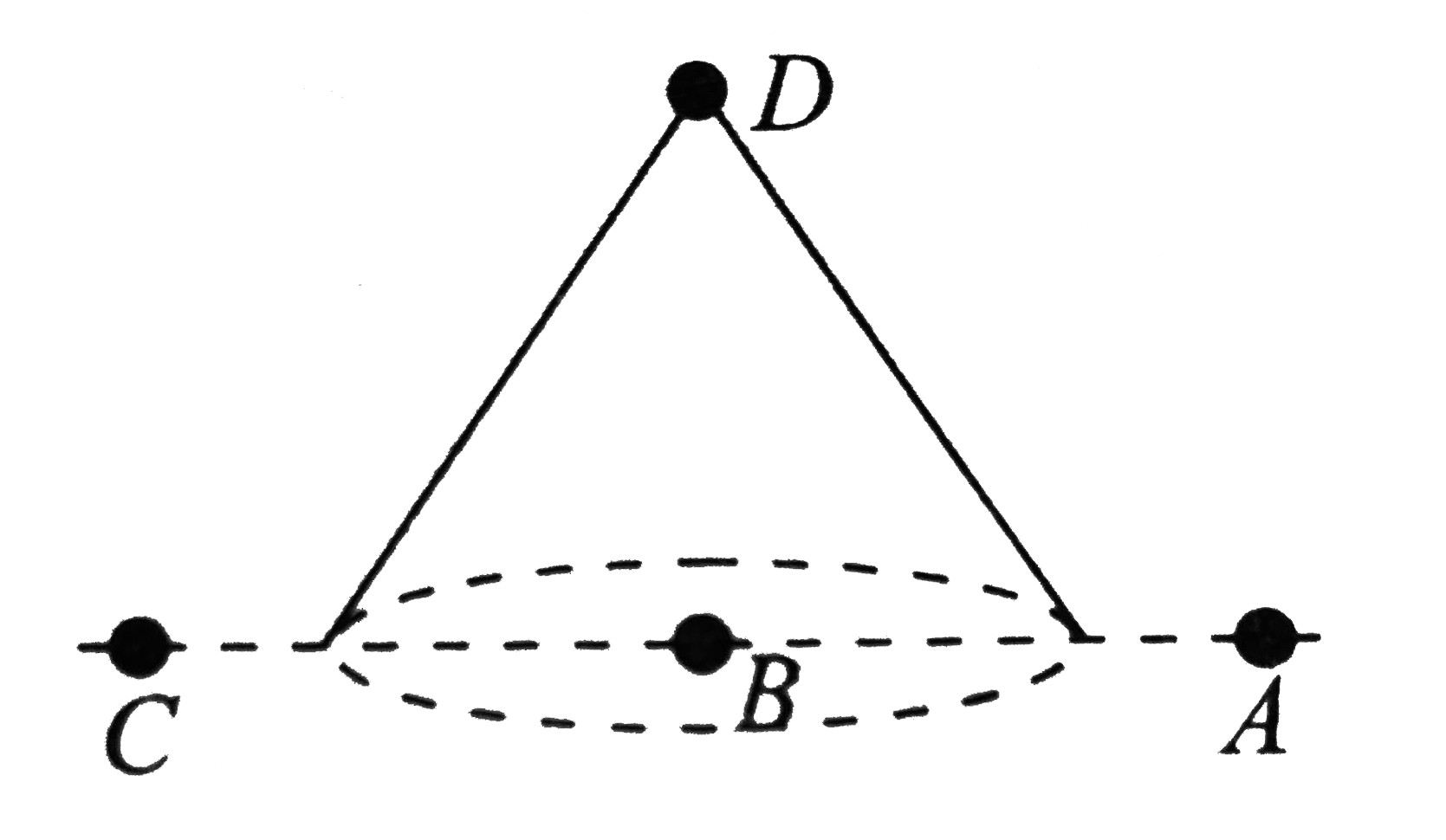
a,b,c, and d, respectively, correspond toView SolutionA right circular imaginary cone is shown in figure A, B, and C are the points in the plane containing the base of the cone, while D is the point at the vertex of the cone. If ϕA,ϕB,ϕCandϕD represent the fulx through the curved surface of the cone when a point charge Q is at points A, B, C, and D. respectively. then.
View Solution