Collision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
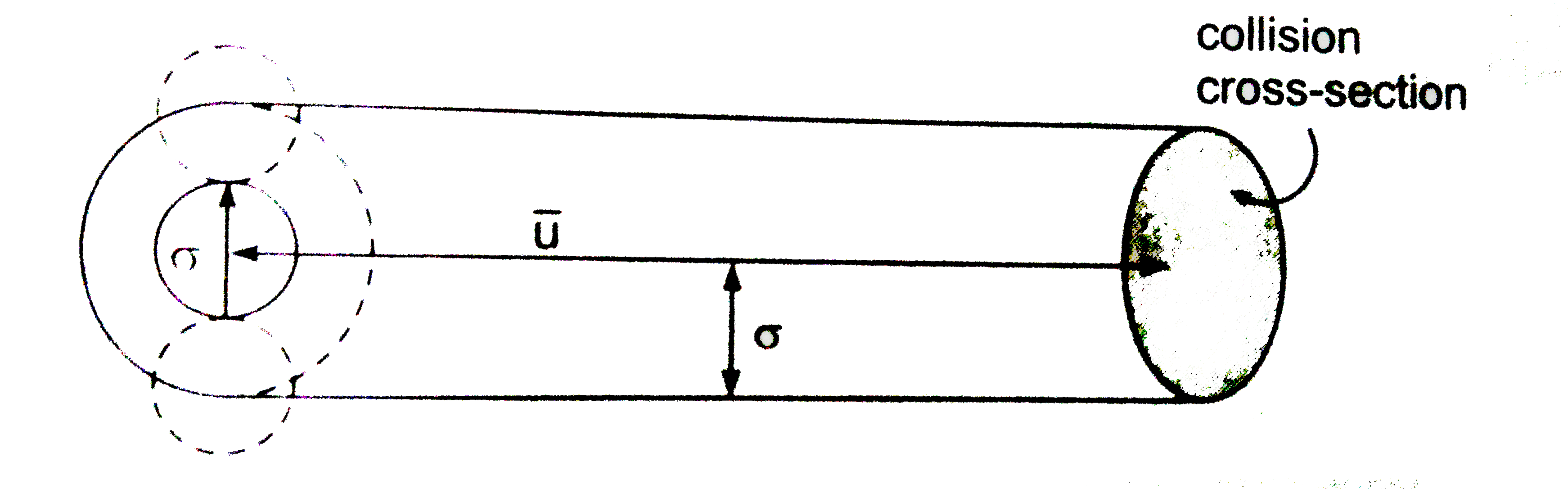
V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.
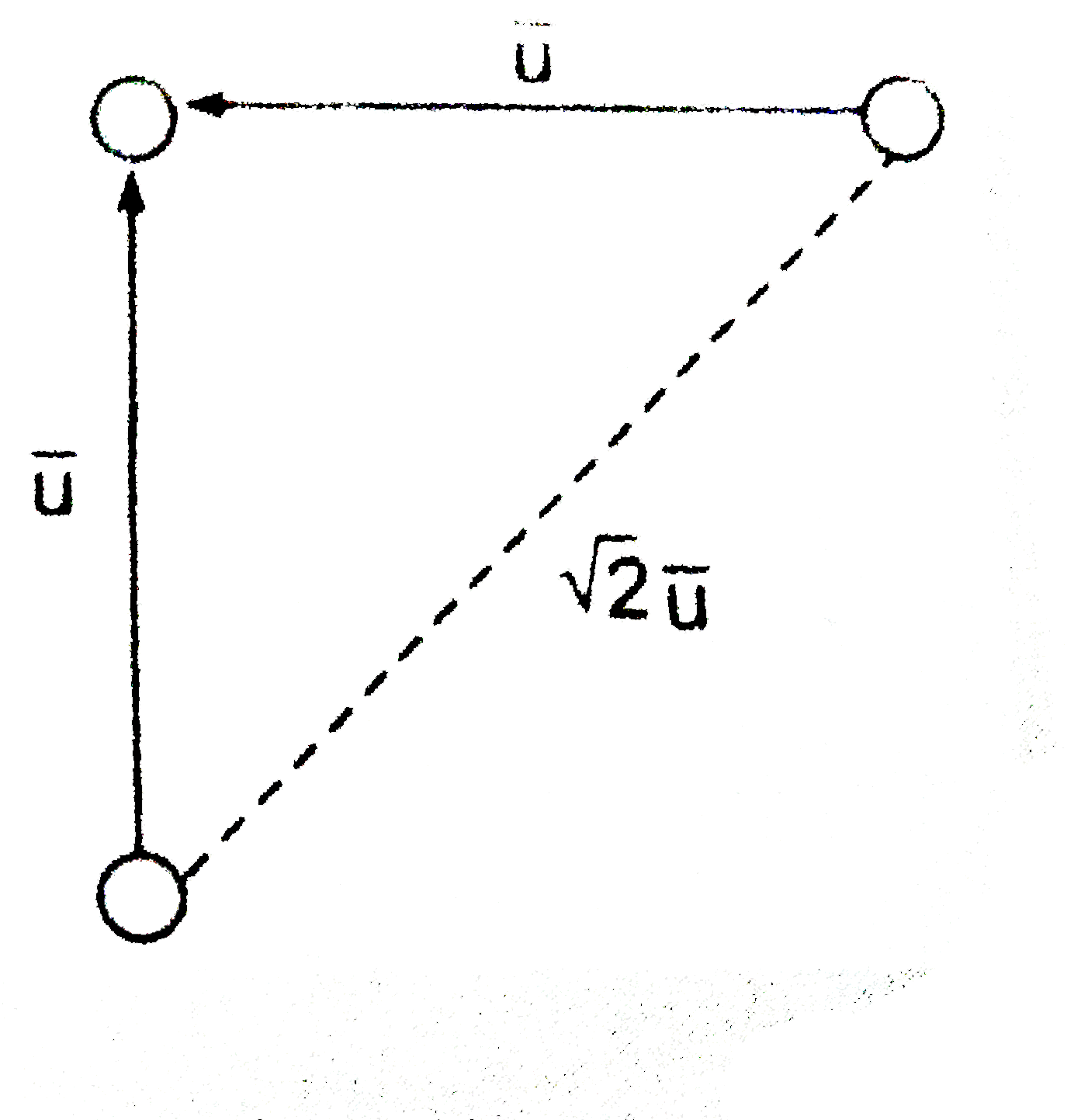
Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯uN∗
The total number of bimolecular collisions Z11 per unit volume per unit time is given by
Z11=12(Z1N∗)orZ11=12(√2πσ2¯uN∗)N∗=1√2πσ2¯uN∗2
If the collsion involve two unlike molecules then the number of collisions Z12 per unit volume per unit time is given as
Z12=πσ212(√8kTπμ)N1N2
where N1 and N2 are the number of molecules per unit volume of the two types of molecules, σ12 is the average diameter of the two molecules and μ is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows :
λ=Average distance travelled per unit timeNO. of collisions made by a single molecule per unit time=¯uZ1
or λ=¯u√2πσ2¯uN∗⇒1√2πσ2¯uN∗
Three ideal gas samples in separate equal volume containers are taken and following data is given :
PressureTemperatureMean free pathsMol.wt.Gas A1atm1600K0.16nm20Gas B2atm200K0.16nm40Gas C4atm400K0.04nm80
Calculate ratio of collision frequencies (Z11)(A:B:C) of following for the three gases.
1:2:4
4:2:1
1:4:16
16:4:1
The correct Answer is:c
(c) Let σA,σB and σC be collision diameters of A,B and C
λ=kT√2πlσ2P,i.e.,σ∝√TλP
∴ σA:σB:σC
=√16000.16×1:√2000.16×2:√4000.04×4
=4:1:2
Z11∝σ2P2√mT3/2
⇒A:B:C=16×1√20×(1600)3/2:
1×4√40×(200)3/2:4×16√80×(400)3/2
=1:4:16
Topper's Solved these Questions
- GASEOUS STATEBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Level 3 Passage 3
4 Videos
- GASEOUS STATEBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - One or More Answers is/are Correct
20 Videos
- GASEOUS STATEBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Level 3 Passage 1
4 Videos
- ELECTROCHEMISTRYBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - Subjective problems
14 Videos
- IONIC EEQUILIBRIUMBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - IONIC EEQUILIBRIUMEXERCISE - Subjective problems
1 Videos
Similar Questions
A monometer contains a liquid of density 5.44g/cm3 is attached to a flask containing gas A'asfollows<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/NRA_PHY_CHM_JMA_C03_E01_213_Q01.pngwh=80%sty≤=background:white;><br>Ifthesameliqusused∈¯ometer→measuretheatmosphericpressure,thenwˆwillbethe≤n>hoftheliquolumn,whichexertspressureequal→1atm?(densityofHg=13.6g//cm^(3))
View SolutionWhich of the following curves represent(s) Boyle's law?
View Solutionvan der Waal's equation for calculating the pressure of a non ideal gas is
(P+an2V2)(V−nb)=nRT
van der Waal's suggested that the pressure exerted by an ideal gas , Pideal, is related to the experiventally measured pressure, Pideal by the equation
Pideal=Preal↑observed pressure+an2V2↑currection term
Constant 'a' is measure of intermolecular interaction between gaseous molecules that gives rise to nonideal behavior. It depends upon how frequently any two molecules approach each other closely. Another correction concerns the volume occupied by the gas molecules. In the ideal gas equation, V represents the volume of the container. However, each molecule does occupy a finite, although small, intrinsic volume, so the effective volume of the gas vecomes (V-nb), where n is the number of moles of the gas and b is a constant. The term nb represents the volume occupied by gas particles present in n moles of the gas .
Having taken into account the corrections for pressure and volume, we can rewrite the ideal gas equation as follows :
(P+an2V2)corrected pressure(V−nb)corrected volume=nRT
AT relatively high pressures, the van der Waals' equation of state reduces to
View SolutionHow many faradays are required for reduction of 1mol C6H5NO2 into C6H5NH2?
View SolutionCalculate pOH of 0.1 M aq. Solution of weak base BOH (Kb=10−7) at 25∘C.
View SolutionIf X is the total number of collisions that a gas molecule registers with other molecules per unit time under particular conditions, then what is the collision frequency of the gas containing N molecules per unit volume is ?
View SolutionThe number of molecules per unit volume (n) of a gas is given by
View SolutionIf X is the total number of collision which a gas molecule registers with others per unit time under particular condions, then the collision frequency of the gas containing N molecules per unit volume is
View SolutionCollision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
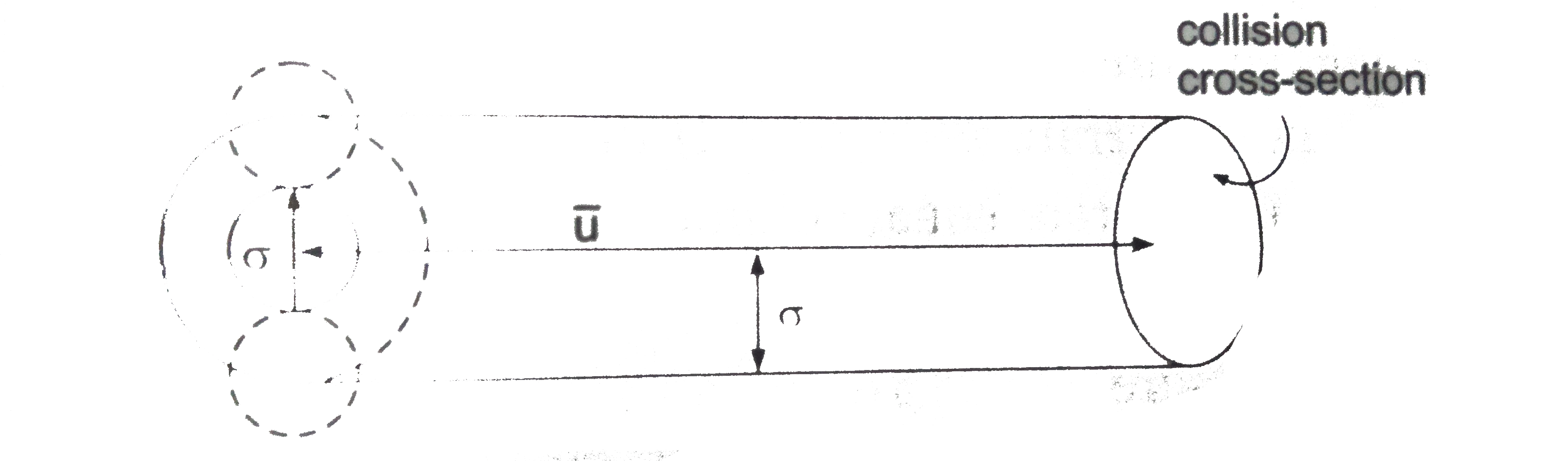
V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.
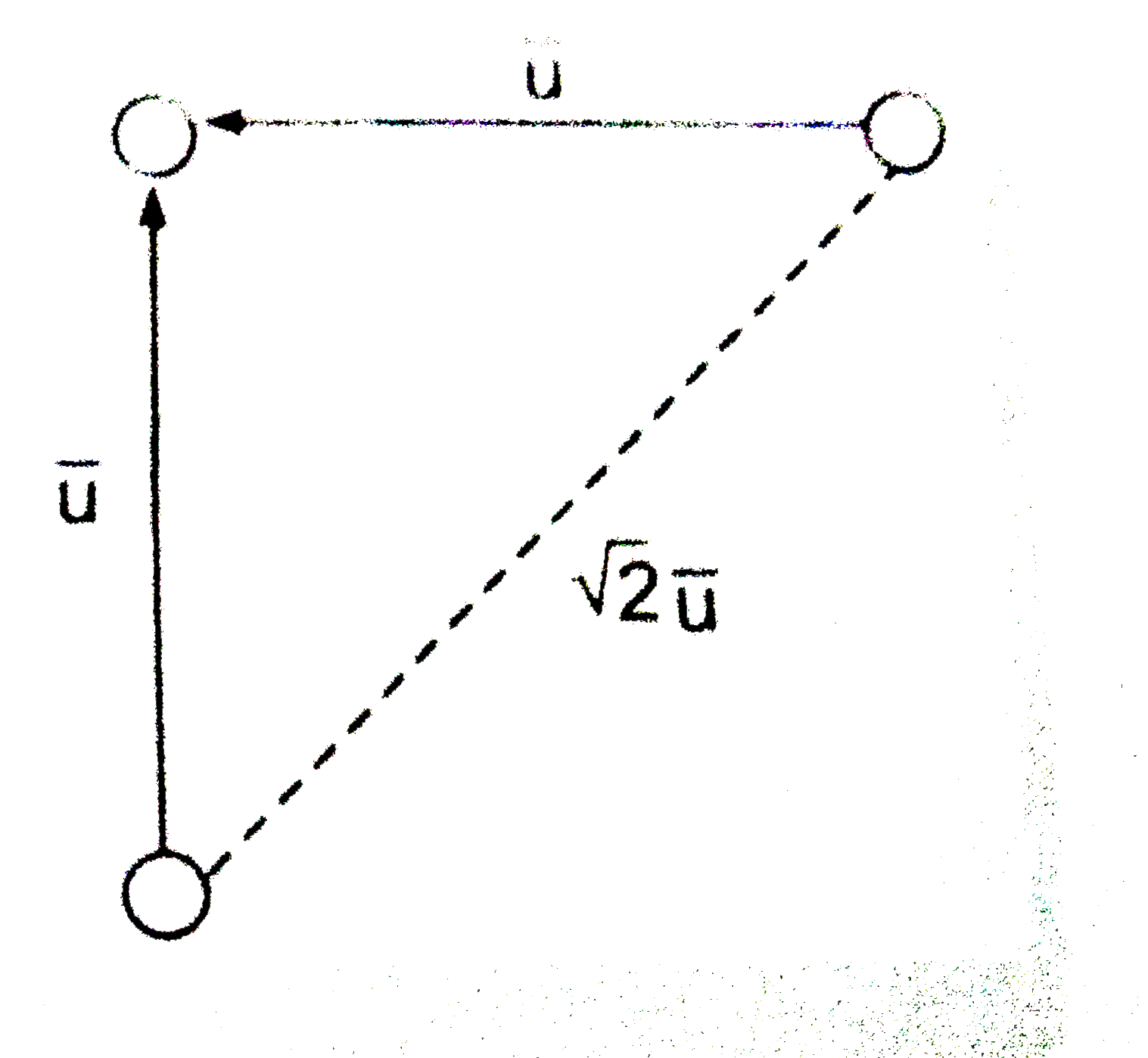
Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯uN∗
The total number of bimolecular collisions Z11 per unit volume per unit time is given by
Z11=12(Z1N∗)orZ11=12(√2πσ2¯uN∗)N∗=1√2πσ2¯uN∗2
If the collsion involve two unlike molecules then the number of collisions Z12 per unit volume per unit time is given as
Z12=πσ212(√8kTπμ)N1N2
where N1 and N2 are the number of molecules per unit volume of the two types of molecules, σ12 is the average diameter of the two molecules and μ is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows :
λ=Average distance travelled per unit timeNO. of collisions made by a single molecule per unit time=¯uZ1
or λ=¯u√2πσ2¯uN∗⇒1√2πσ2¯uN∗
For a given gas the mean free path at a particular pressure is :
View SolutionCollision cross-section is an area of an imaginary sphere of radius sigma around the molecule within which the centre of another molecule cannot penetrate. The volume swept by a single molecule in unit time is V=(pisigma^(2))overline(u) where overline(u) is the average speed If N^(**) is the number of molecules per unit volume, then the number of molecules within the volume V is N=VN^(**)=(pisigma^(2)overline(u))N^(**) Hence, the number of collision made by a single molecule in unit time will be Z=N=(pi sigma^(2)overline(u))N^(**) In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is sqrt(2)overline(u) as shown below. Number of collision made by a single molecule with other molecule per unit time is given by Z_(1)=pisigma^(2)(overline(u)_("rel"))N^(**)=sqrt(2) pisigma^(2)overline(u)N^(**) The total number of bimolecular collisions Z_(11) per unit volume per unit time is given by Z_(11)=(1)/(2)(Z_(1)N^(**))"or" Z_(11)=(1)/(2)(sqrt(2)pisigma^(2)overline(u)N^(**))N^(**)=(1)/(sqrt(2))pisigma^(2)overline(u)N^(**2) If the collsion involve two unlike molecules then the number of collisions Z_(12) per unit volume per unit time is given as Z_(12)= pisigma _(12)^(2)(sqrt((8kT)/(pimu)))N_(1)N_(2) where N_(1) and N_(2) are the number of molecules per unit volume of the two types of molecules, sigma_(12) is the average diameter of the two molecules and mu is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows : lambda=("Average distance travelled per unit time")/("NO. of collisions made by a single molecule per unit time")=(overline(u))/(Z_(1)) "or "lambda=(overline(u))/(sqrt(2)pisigma^(2)overline(u)N^(**))implies(1)/(sqrt(2)pisigma^(2)overline(u)N^(**)) Three ideal gas samples in separate equal volume containers are taken and following data is given : {:(" ","Pressure","Temperature","Mean free paths","Mol.wt."),("Gas A",1atm,1600K,0.16nm,20),("Gas B",2atm,200K,0.16nm,40),("Gas C",4atm,400K,0.04nm,80):} Calculate ratio of collision frequencies (Z_(11)) (A:B:C) of following for the three gases.
View SolutionCollision cross-section is an area of an imaginary sphere of radius sigma around the molecule within which the centre of another molecule cannot penetrate. The volume swept by a single molecule in unit time is V=(pisigma^(2))overline(u) where overline(u) is the average speed If N^(**) is the number of molecules per unit volume, then the number of molecules within the volume V is N=VN^(**)=(pisigma^(2)overline(u))N^(**) Hence, the number of collision made by a single molecule in unit time will be Z=N=(pi sigma^(2)overline(u))N^(**) In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is sqrt(2)overline(u) as shown below. Number of collision made by a single molecule with other molecule per unit time is given by Z_(1)=pisigma^(2)(overline(u)_("rel"))N^(**)=sqrt(2) pisigma^(2)overline(2)N^(**) The total number of bimolecular collisions Z_(1) per unit volume per unit time is given by Z_(1)=(1)/(2)(Z_(1)N^(**))or Z_(11)=(1)/(2)(sqrt(2)pisigma^(2)overline(u)N^(**))N^(**)=(1)/(sqrt(2))pisigma^(2)overline(u)N^(**2) If the collsion involve two unlike molecules then the number of collisions Z_(12) per unit volume per unit time is given as Z_(12)= pisigma _(12)^(2)(sqrt((8kT)/(pimu)))N_(1)N_(2) where N_(1) and N_(2) are the number of molecules per unit volume of the two types of molecules, sigma_(12) is the average diameter of the two molecules and mu is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows : lambda=("Average distance travelled per unit time")/("NO. of collisions made by a single molecule per unit time")=(overline(u))/(Z_(1)) or" "lambda=(overline(u))/(sqrt(2)pisigma^(2)overline(u)N^(**))implies(1)/(sqrt(2)pisigma^(2)overline(u)N^(**)) Three ideal gas samples in separate equal volume containers are taken and following data is given : {:(" ","Pressure","Temperature","Mean free paths","Mol.wt."),("Gas A",1atm,1600K,0.16nm,20),("Gas B",2atm,200K,0.16nm,40),("Gas C",4atm,400K,0.04nm,80):} Calculate number of collision by one molecule per sec (Z_(1)) .
View SolutionCollision cross-section is an area of an imaginary sphere of radius sigma around the molecule within which the centre of another molecule cannot penetrate. The volume swept by a single molecule in unit time is V=(pisigma^(2))overline(u) where overline(u) is the average speed If N^(**) is the number of molecules per unit volume, then the number of molecules within the volume V is N=VN^(**)=(pisigma^(2)overline(u))N^(**) Hence, the number of collision made by a single molecule in unit time will be Z=N=(pi sigma^(2)overline(u))N^(**) In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is sqrt(2)overline(u) as shown below. Number of collision made by a single molecule with other molecule per unit time is given by Z_(1)=pisigma^(2)(overline(u)_("rel"))N^(**)=sqrt(2) pisigma^(2)overline(u)N^(**) The total number of bimolecular collisions Z_(11) per unit volume per unit time is given by Z_(11)=(1)/(2)(Z_(1)N^(**))"or" Z_(11)=(1)/(2)(sqrt(2)pisigma^(2)overline(u)N^(**))N^(**)=(1)/(sqrt(2))pisigma^(2)overline(u)N^(**2) If the collsion involve two unlike molecules then the number of collisions Z_(12) per unit volume per unit time is given as Z_(12)= pisigma _(12)^(2)(sqrt((8kT)/(pimu)))N_(1)N_(2) where N_(1) and N_(2) are the number of molecules per unit volume of the two types of molecules, sigma_(12) is the average diameter of the two molecules and mu is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows : lambda=("Average distance travelled per unit time")/("NO. of collisions made by a single molecule per unit time")=(overline(u))/(Z_(1)) "or "lambda=(overline(u))/(sqrt(2)pisigma^(2)overline(u)N^(**))implies(1)/(sqrt(2)pisigma^(2)overline(u)N^(**)) Three ideal gas samples in separate equal volume containers are taken and following data is given : {:(" ","Pressure","Temperature","Mean free paths","Mol.wt."),("Gas A",1atm,1600K,0.16nm,20),("Gas B",2atm,200K,0.16nm,40),("Gas C",4atm,400K,0.04nm,80):} Calculate number of collision by one molecule per sec (Z_(1)) .
View SolutionLet the vectors ¯u,¯v,¯¯¯w be coplanar, , then ¯u⋅(¯vׯ¯¯w)=
View SolutionIf ¯u=ˆi−2ˆj+ˆk,¯v=3ˆi+ˆk,¯¯¯w=ˆj−ˆk, then (¯u+¯¯¯w)⋅((¯uׯv)×(¯vׯ¯¯w))=
View SolutionIf ¯u,¯v,¯¯¯w are three non-coplanar vectors, then (¯u+¯v−¯¯¯w)⋅((¯u−¯v)×(¯v−¯¯¯w))=
View Solution
