Collision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
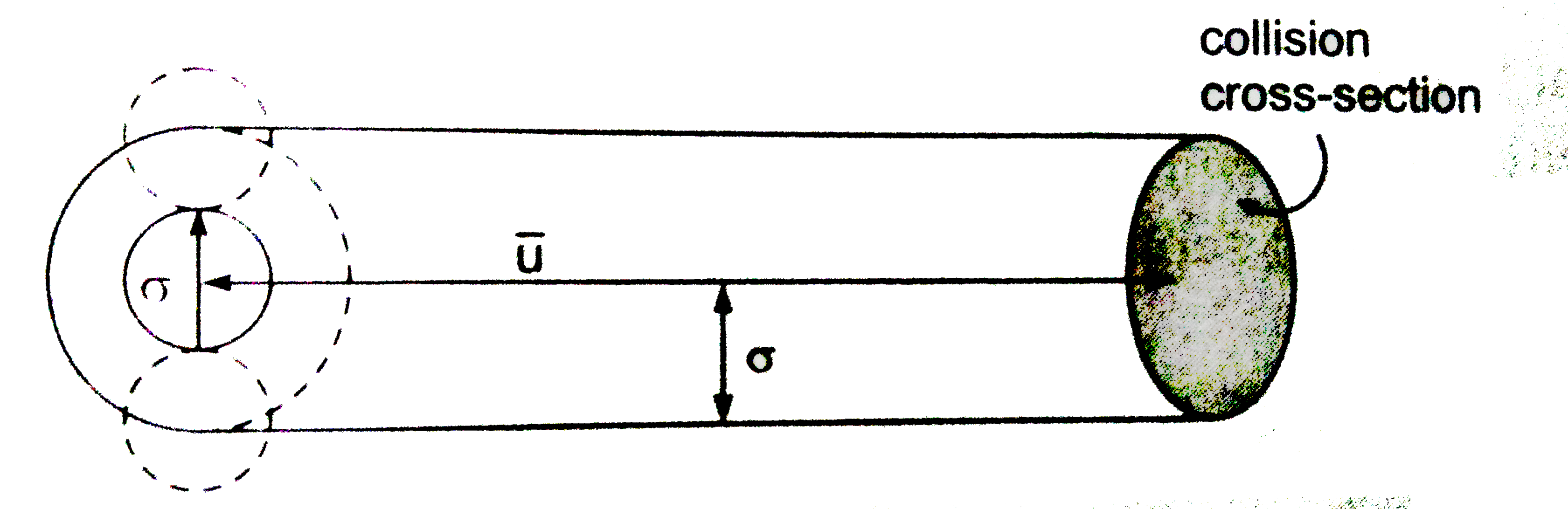
V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.
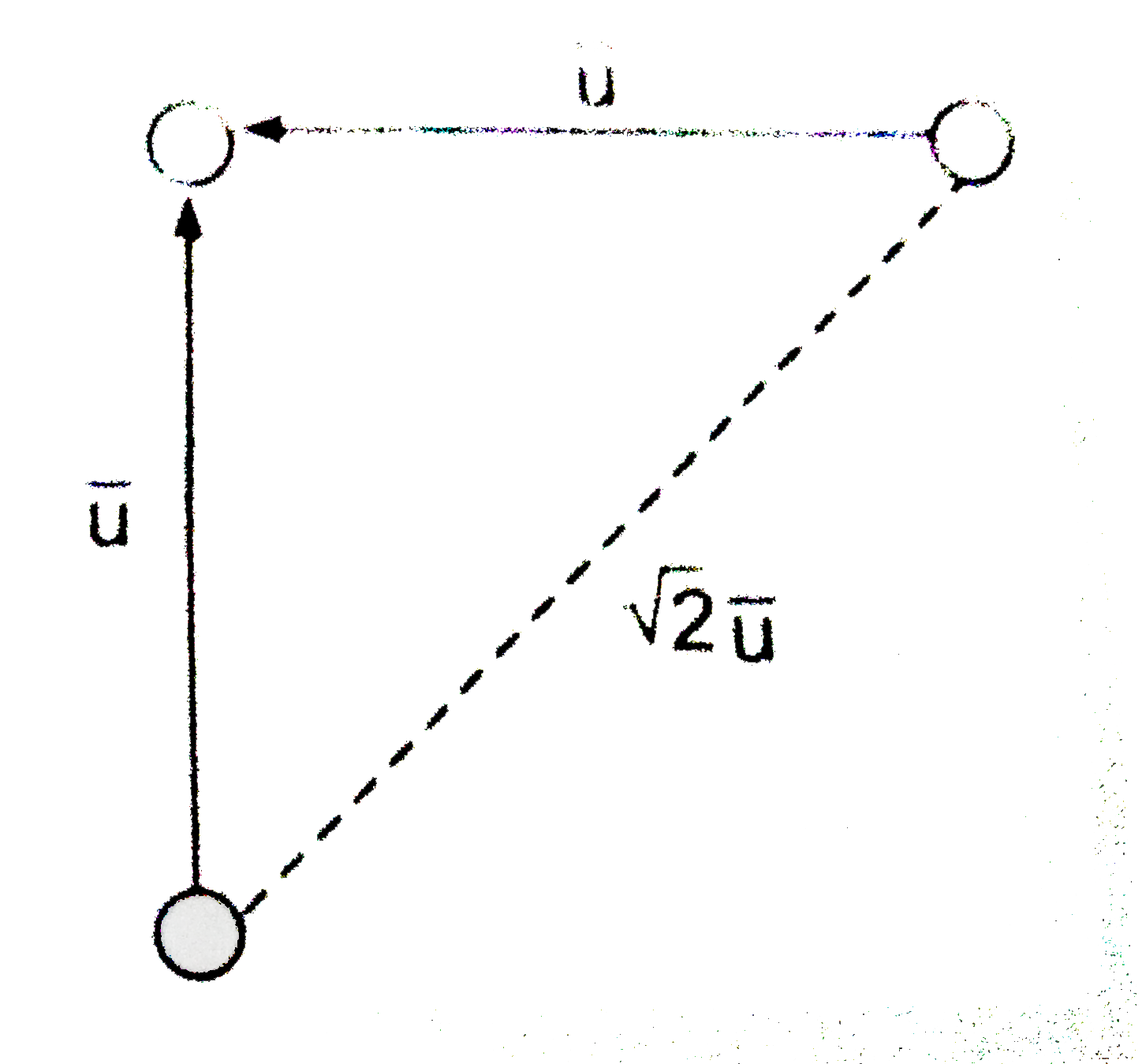
Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯2N∗
The→talνmberofbimo≤ca––rcollisionsZ_(1)perunitvolumeperunittimeisgivenby<br>Z_(1)=(1)/(2)(Z_(1)N^(**))or Z_(11)=(1)/(2)(sqrt(2)pisigma^(2)overline(u)N^(**))N^(**)=(1)/(sqrt(2))pisigma^(2)overline(u)N^(**2)<br>Ifthecollsion∈volvetwounlikemo≤ce–sthentheνmberofcollisionsZ_(12)perunitvolumeperunittimeisgivenas<br>Z_(12)= pisigma _(12)^(2)(sqrt((8kT)/(pimu)))N_(1)N_(2)<br>whereN_(1)andN_(2)aretheνmberofmo≤ce–sperunitvolumeofthetwotypesofmo≤ce–s,sigma_(12)istheavera≥diameterofthetwomo≤ce–sandmuisthereducedmass.Themeaneepathistheavera≥distancetravel≤dbyamo≤ce–betweentwo≻essivecollisions.Wecanexpressitasfollows:<br>lambda=("Average distance travelled per unit time")/("NO. of collisions made by a single molecule per unit time")=(overline(u))/(Z_(1))<br>or" "lambda=(overline(u))/(sqrt(2)pisigma^(2)overline(u)N^(**))implies(1)/(sqrt(2)pisigma^(2)overline(u)N^(**))<br>Threealgassamp≤s∈separateequalvolumeconta∈ersaretakenandfollow∈gdataisgiven:<br> PressureTemperatureMean free pathsMol.wt.Gas A1atm1600K0.16nm20Gas B2atm200K0.16nm40Gas C4atm400K0.04nm80
Calculate number of collision by one molecule per sec (Z1).Solution in Telugu
4:1:4
1:4:4
4:3:2
1:2:4
Step by step video, text & image solution for Collision cross-section is an area of an imaginary sphere of radius sigma around the molecule within which the centre of another molecule cannot penetrate. The volume swept by a single molecule in unit time is V=(pisigma^(2))overline(u) where overline(u) is the average speed If N^(**) is the number of molecules per unit volume, then the number of molecules within the volume V is N=VN^(**)=(pisigma^(2)overline(u))N^(**) Hence, the number of collision made by a single molecule in unit time will be Z=N=(pi sigma^(2)overline(u))N^(**) In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is sqrt(2)overline(u) as shown below. Number of collision made by a single molecule with other molecule per unit time is given by Z_(1)=pisigma^(2)(overline(u)_("rel"))N^(**)=sqrt(2) pisigma^(2)overline(2)N^(**) The total number of bimolecular collisions Z_(1) per unit volume per unit time is given by Z_(1)=(1)/(2)(Z_(1)N^(**))or Z_(11)=(1)/(2)(sqrt(2)pisigma^(2)overline(u)N^(**))N^(**)=(1)/(sqrt(2))pisigma^(2)overline(u)N^(**2) If the collsion involve two unlike molecules then the number of collisions Z_(12) per unit volume per unit time is given as Z_(12)= pisigma _(12)^(2)(sqrt((8kT)/(pimu)))N_(1)N_(2) where N_(1) and N_(2) are the number of molecules per unit volume of the two types of molecules, sigma_(12) is the average diameter of the two molecules and mu is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows : lambda=("Average distance travelled per unit time")/("NO. of collisions made by a single molecule per unit time")=(overline(u))/(Z_(1)) or" "lambda=(overline(u))/(sqrt(2)pisigma^(2)overline(u)N^(**))implies(1)/(sqrt(2)pisigma^(2)overline(u)N^(**)) Three ideal gas samples in separate equal volume containers are taken and following data is given : {:(" ","Pressure","Temperature","Mean free paths","Mol.wt."),("Gas A",1atm,1600K,0.16nm,20),("Gas B",2atm,200K,0.16nm,40),("Gas C",4atm,400K,0.04nm,80):} Calculate number of collision by one molecule per sec (Z_(1)). by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GASEOUS STATEBOOK - NARENDRA AWASTHICHAPTER - GASEOUS STATEEXERCISE - Level 1 (Q.31 To Q.60)
1 Videos
- GASEOUS STATEBOOK - NARENDRA AWASTHICHAPTER - GASEOUS STATEEXERCISE - Level 1 (Q.121 To Q.150)
1 Videos
- ELECTROCHEMISTRYBOOK - NARENDRA AWASTHICHAPTER - ELECTROCHEMISTRYEXERCISE - Level 3 - Subjective Problems
1 Videos
- IONIC EEQUILIBRIUMBOOK - NARENDRA AWASTHICHAPTER - IONIC EEQUILIBRIUMEXERCISE - Assertin-Reason Type Questions
1 Videos
Similar Questions
Nitrogen forms several gaseous oxides. One of them has a density of 1.33 g/L measured 764 mmHg and 150∘C. Write the formula of the compound.
View SolutionDimethyl ether decomposes as
CH3OCH3(g)→CH4(g)+CO(g)+H2(g)
When CH3OCH3(g) decomposes to 20% extent under certain conditions, what is the ratio of diffusion of pure CH3OCH3(g) with methane?
View SolutionA solution containing 1MXSO4(aq) and 1MYSO4(aq) is electrolysed. If conc. Of X2+ is 10−zM when deposition Y2+ and X2+ starts simultaneously, calculate the value of Z.
Given: 2.303RTF=0.06
E∘x2+|X=−0.12V,E∘Y2+|Y=−0.24V
View SolutionSTATEMENT-1: All strong monoprotic acid with same concentration in dilute solution show same pH.
STATEMENT-2: Water shows levelling effect.
View SolutionIf X is the total number of collisions that a gas molecule registers with other molecules per unit time under particular conditions, then what is the collision frequency of the gas containing N molecules per unit volume is ?
View SolutionThe number of molecules per unit volume (n) of a gas is given by
View SolutionIf X is the total number of collision which a gas molecule registers with others per unit time under particular condions, then the collision frequency of the gas containing N molecules per unit volume is
View SolutionCollision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
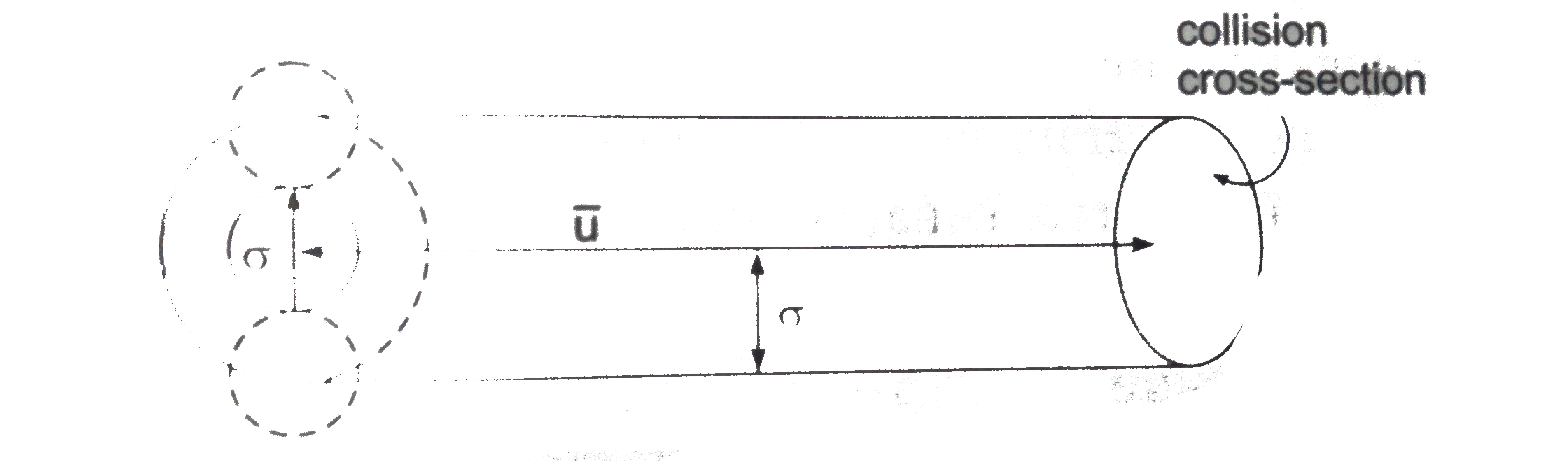
V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.

Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯uN∗
The total number of bimolecular collisions Z11 per unit volume per unit time is given by
Z11=12(Z1N∗)orZ11=12(√2πσ2¯uN∗)N∗=1√2πσ2¯uN∗2
If the collsion involve two unlike molecules then the number of collisions Z12 per unit volume per unit time is given as
Z12=πσ212(√8kTπμ)N1N2
where N1 and N2 are the number of molecules per unit volume of the two types of molecules, σ12 is the average diameter of the two molecules and μ is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows :
λ=Average distance travelled per unit timeNO. of collisions made by a single molecule per unit time=¯uZ1
or λ=¯u√2πσ2¯uN∗⇒1√2πσ2¯uN∗
For a given gas the mean free path at a particular pressure is :
View SolutionCollision cross-section is an area of an imaginary sphere of radius sigma around the molecule within which the centre of another molecule cannot penetrate. The volume swept by a single molecule in unit time is V=(pisigma^(2))overline(u) where overline(u) is the average speed If N^(**) is the number of molecules per unit volume, then the number of molecules within the volume V is N=VN^(**)=(pisigma^(2)overline(u))N^(**) Hence, the number of collision made by a single molecule in unit time will be Z=N=(pi sigma^(2)overline(u))N^(**) In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is sqrt(2)overline(u) as shown below. Number of collision made by a single molecule with other molecule per unit time is given by Z_(1)=pisigma^(2)(overline(u)_("rel"))N^(**)=sqrt(2) pisigma^(2)overline(u)N^(**) The total number of bimolecular collisions Z_(11) per unit volume per unit time is given by Z_(11)=(1)/(2)(Z_(1)N^(**))"or" Z_(11)=(1)/(2)(sqrt(2)pisigma^(2)overline(u)N^(**))N^(**)=(1)/(sqrt(2))pisigma^(2)overline(u)N^(**2) If the collsion involve two unlike molecules then the number of collisions Z_(12) per unit volume per unit time is given as Z_(12)= pisigma _(12)^(2)(sqrt((8kT)/(pimu)))N_(1)N_(2) where N_(1) and N_(2) are the number of molecules per unit volume of the two types of molecules, sigma_(12) is the average diameter of the two molecules and mu is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows : lambda=("Average distance travelled per unit time")/("NO. of collisions made by a single molecule per unit time")=(overline(u))/(Z_(1)) "or "lambda=(overline(u))/(sqrt(2)pisigma^(2)overline(u)N^(**))implies(1)/(sqrt(2)pisigma^(2)overline(u)N^(**)) Three ideal gas samples in separate equal volume containers are taken and following data is given : {:(" ","Pressure","Temperature","Mean free paths","Mol.wt."),("Gas A",1atm,1600K,0.16nm,20),("Gas B",2atm,200K,0.16nm,40),("Gas C",4atm,400K,0.04nm,80):} Calculate ratio of collision frequencies (Z_(11)) (A:B:C) of following for the three gases.
View SolutionCollision cross-section is an area of an imaginary sphere of radius sigma around the molecule within which the centre of another molecule cannot penetrate. The volume swept by a single molecule in unit time is V=(pisigma^(2))overline(u) where overline(u) is the average speed If N^(**) is the number of molecules per unit volume, then the number of molecules within the volume V is N=VN^(**)=(pisigma^(2)overline(u))N^(**) Hence, the number of collision made by a single molecule in unit time will be Z=N=(pi sigma^(2)overline(u))N^(**) In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is sqrt(2)overline(u) as shown below. Number of collision made by a single molecule with other molecule per unit time is given by Z_(1)=pisigma^(2)(overline(u)_("rel"))N^(**)=sqrt(2) pisigma^(2)overline(2)N^(**) The total number of bimolecular collisions Z_(1) per unit volume per unit time is given by Z_(1)=(1)/(2)(Z_(1)N^(**))or Z_(11)=(1)/(2)(sqrt(2)pisigma^(2)overline(u)N^(**))N^(**)=(1)/(sqrt(2))pisigma^(2)overline(u)N^(**2) If the collsion involve two unlike molecules then the number of collisions Z_(12) per unit volume per unit time is given as Z_(12)= pisigma _(12)^(2)(sqrt((8kT)/(pimu)))N_(1)N_(2) where N_(1) and N_(2) are the number of molecules per unit volume of the two types of molecules, sigma_(12) is the average diameter of the two molecules and mu is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows : lambda=("Average distance travelled per unit time")/("NO. of collisions made by a single molecule per unit time")=(overline(u))/(Z_(1)) or" "lambda=(overline(u))/(sqrt(2)pisigma^(2)overline(u)N^(**))implies(1)/(sqrt(2)pisigma^(2)overline(u)N^(**)) Three ideal gas samples in separate equal volume containers are taken and following data is given : {:(" ","Pressure","Temperature","Mean free paths","Mol.wt."),("Gas A",1atm,1600K,0.16nm,20),("Gas B",2atm,200K,0.16nm,40),("Gas C",4atm,400K,0.04nm,80):} Calculate number of collision by one molecule per sec (Z_(1)) .
View SolutionCollision cross-section is an area of an imaginary sphere of radius sigma around the molecule within which the centre of another molecule cannot penetrate. The volume swept by a single molecule in unit time is V=(pisigma^(2))overline(u) where overline(u) is the average speed If N^(**) is the number of molecules per unit volume, then the number of molecules within the volume V is N=VN^(**)=(pisigma^(2)overline(u))N^(**) Hence, the number of collision made by a single molecule in unit time will be Z=N=(pi sigma^(2)overline(u))N^(**) In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is sqrt(2)overline(u) as shown below. Number of collision made by a single molecule with other molecule per unit time is given by Z_(1)=pisigma^(2)(overline(u)_("rel"))N^(**)=sqrt(2) pisigma^(2)overline(u)N^(**) The total number of bimolecular collisions Z_(11) per unit volume per unit time is given by Z_(11)=(1)/(2)(Z_(1)N^(**))"or" Z_(11)=(1)/(2)(sqrt(2)pisigma^(2)overline(u)N^(**))N^(**)=(1)/(sqrt(2))pisigma^(2)overline(u)N^(**2) If the collsion involve two unlike molecules then the number of collisions Z_(12) per unit volume per unit time is given as Z_(12)= pisigma _(12)^(2)(sqrt((8kT)/(pimu)))N_(1)N_(2) where N_(1) and N_(2) are the number of molecules per unit volume of the two types of molecules, sigma_(12) is the average diameter of the two molecules and mu is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows : lambda=("Average distance travelled per unit time")/("NO. of collisions made by a single molecule per unit time")=(overline(u))/(Z_(1)) "or "lambda=(overline(u))/(sqrt(2)pisigma^(2)overline(u)N^(**))implies(1)/(sqrt(2)pisigma^(2)overline(u)N^(**)) Three ideal gas samples in separate equal volume containers are taken and following data is given : {:(" ","Pressure","Temperature","Mean free paths","Mol.wt."),("Gas A",1atm,1600K,0.16nm,20),("Gas B",2atm,200K,0.16nm,40),("Gas C",4atm,400K,0.04nm,80):} Calculate number of collision by one molecule per sec (Z_(1)) .
View SolutionLet the vectors ¯u,¯v,¯¯¯w be coplanar, , then ¯u⋅(¯vׯ¯¯w)=
View SolutionIf ¯u=ˆi−2ˆj+ˆk,¯v=3ˆi+ˆk,¯¯¯w=ˆj−ˆk, then (¯u+¯¯¯w)⋅((¯uׯv)×(¯vׯ¯¯w))=
View SolutionIf ¯u,¯v,¯¯¯w are three non-coplanar vectors, then (¯u+¯v−¯¯¯w)⋅((¯u−¯v)×(¯v−¯¯¯w))=
View Solutionयदि प्रति एकांक आयतन अणुओं की संख्या n है तो आदर्श गैस समीकरण लिखिए ।
View SolutionAn ideal gas of N molecules occupies a volume V. The average kinetic energy per molecule is u . If P denotes the pressure of the gas, then
View Solution
