Explain three dimensional close packing from two dimensional hexagonal close packing.

Text Solution

Verified by Experts

In hexagonal close packing layer in two dimensions, there are two sets of triangular voids. The three dimensional arrangement is obtained by stacking the two dimensional hexagonal layers one above the other.

Over the first layer (say "A") of two dimensional hexagonal arrangement, if the second layer (say "B") is placed, the one set of triangular void of layer "A" is covered by the spheres of layer "B".

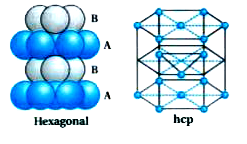
Over the second layer "B", there are again two sets of triangular voids. If the third layer is placed over the triangular voids of second layer such that the spheres of third layer an first layer in exact alignment, the hexagonal close packing in three dimensional is obtained.

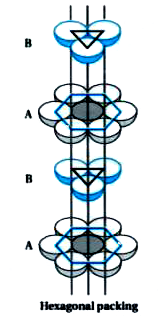
The third layer and first layer are exactly same and hence it is called "A" type. Thus the arrangement obtained is ABABAB.... Pattern.
Ex. : Zn and Mg shows this type of arrangement.
.
If the third layer of the spheres are placed over the triangular voids of the second layer that are formed just above the unoccupied voids of the first layer, the face cubic centred unit cell is formed.
The third layer is different from layers A and B. Hence, if the third layer is called "C", the arrangement obtained is ABCABCABC... ie., fourth layer of sphere and first layer of spheres are exactly same.

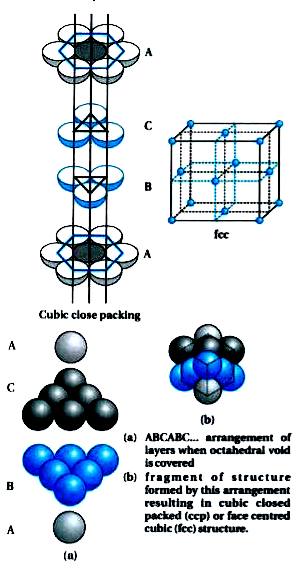
Ex. : Metals such as Cu, Ag, etc. crystallizes in FCC structure.
In both type of close packing structures, the packing efficiency is 74% and co-ordination number is 12.

Updated on:21/07/2023

Class 12 CHEMISTRY SOLID STATE

Topper's Solved these Questions

Knowledge Check

Three-dimensional close packing in solids is referred to as stacking the second square closed packing exactly above the first. In this tight packing, the spheres are horizontally and vertically correctly balanced. Similarly, we can obtain a simple cubic lattice by adding more layers, one above the other. This can be done in two ways. Three-dimensional close packing from two-dimensional square close-packed layers: By putting the second square closed packing exactly above the first, it is possible to form three-dimensional close packing. In this tight packing, the spheres are horizontally and vertically correctly balanced. Similarly, we can obtain a simple cubic lattice by adding more layers, one above the other.Three-dimensional close packing from two-dimensional hexagonal close-packed layers: With the assistance, of two-dimensional hexagonal packed layers, three-dimensional close packing can be obtained.
The coordination number of cubic closed packing is:
A6
B8
C12
D4
Three-dimensional close packing in solids is referred to as stacking the second square closed packing exactly above the first. In this tight packing, the spheres are horizontally and vertically correctly balanced. Similarly, we can obtain a simple cubic lattice by adding more layers, one above the other. This can be done in two ways. Three-dimensional close packing from two-dimensional square close-packed layers: By putting the second square closed packing exactly above the first, it is possible to form three-dimensional close packing. In this tight packing, the spheres are horizontally and vertically correctly balanced. Similarly, we can obtain a simple cubic lattice by adding more layers, one above the other.Three-dimensional close packing from two-dimensional hexagonal close-packed layers: With the assistance, of two-dimensional hexagonal packed layers, three-dimensional close packing can be obtained.
The correct statement about zns crystal is:
ACoordinate number (6:4): hcp, $Z n^{2 +}$ ions in all octahedral voids
BCoordinate number (6:6): hcp, $Z n^{2 +}$ ions in all tetrahedral voids
CCoordinate number (4:4): ccp, $Z n^{2 +}$ ions in the alternate tetrahedral voids
DCoordinate number (4:4): ccp, $Z n^{2 +}$ ions in all tetrahedral voids
Three-dimensional close packing in solids is referred to as stacking the second square closed packing exactly above the first. In this tight packing, the spheres are horizontally and vertically correctly balanced. Similarly, we can obtain a simple cubic lattice by adding more layers, one above the other. This can be done in two ways. Three-dimensional close packing from two-dimensional square close-packed layers: By putting the second square closed packing exactly above the first, it is possible to form three-dimensional close packing. In this tight packing, the spheres are horizontally and vertically correctly balanced. Similarly, we can obtain a simple cubic lattice by adding more layers, one above the other.Three-dimensional close packing from two-dimensional hexagonal close-packed layers: With the assistance, of two-dimensional hexagonal packed layers, three-dimensional close packing can be obtained.
What will be the ratio of radii of the spheres in cubic systems simple cubic, body centred cubic and face centred cubic systems. if 'a' stands for the edge length.
A $\frac{1}{2} a : \frac{\sqrt{3}}{4} a : \frac{1}{2 \sqrt{2}} a$
B $\frac{1}{2} a : \sqrt{3} a : \frac{1}{\sqrt{2}} a$
C $1 a : \sqrt{3} a : \sqrt{2} a$
D $\frac{1}{2} a : \frac{\sqrt{3}}{2} a : \frac{\sqrt{2}}{2} a$

KUMAR PRAKASHAN-THE SOLID STATE-SECTION - A (QUESTIONS)

Home
Ask Doubt
Profile

Explain three dimensional close packing from two dimensional hexagonal close packing.

Topper's Solved these Questions

Similar Questions

Knowledge Check

KUMAR PRAKASHAN-THE SOLID STATE-SECTION - A (QUESTIONS)