In Schrodinger wave mechanical model Ψ2(r,θ,ϕ) represents :Solution in Telugu
amplitude of electron wave
probability density of electron
total probaility of finding electron around nucleus
orbit
Step by step video & image solution for In Schrodinger wave mechanical model Psi^(2)(r,theta,phi) represents : by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
For similar orbitals having different values of n:
08:27View SolutionA small particle of mass m moves in such a way that the potential energy U = ar2 where a is a constant and r is the distance of the particle from the origin. Assuming Bohr's model of quantization of angular momentum and circular orbits, find the radius of nth allowed orbit.
02:36View SolutionCalculate ΔrG for the reaction at 27∘C
H2(g)+2Ag+(aq)⇔2Ag(s)+2H+(aq)
Given : PH2=0.5 bar, [Ag+]=10−5M,
[H+]=10−3M,ΔrG∘[Ag+(aq)]=77.1kJ/mol02:56View SolutionGiven that (sec theta+tan theta)(sec phi+tan phi)(sec psi+tan psi)=(sec theta-tan theta)(sec phi-tan phi)(sec psi-tan psi) then Prove that value of each side +-1 is
02:50View SolutionIn Schrodinger wave mechanical model Ψ2(r,θ,ϕ) represents :
01:49View SolutionIn schrodinger wave equation ∇2ψ+?π2mh2(E−V)ψ=0 ? is- "
View SolutionIf x=cosθcosϕ+sinθsinϕcosψ,y=cosθsinϕ−sinθcosϕcosψ and z=sinθsinψ, then x2+y2+z2 equals :
02:46View SolutionIn Schrodinger wave mechanical model Ψ2(r,θ,ϕ) represents :
00:54View SolutionWhen Schrodinger wave equation in polar coordinates is solved the solution for Phi is of the form Psi (r, theta , phi)= R(r) , Y(theta , phi) . Here R(r) is radial part of wave function and Y(theta, phi) is angular part of the wave function. The region or space where probability of finding electron is zero is called nodal surface. If the probability of finding electron is zero then Psi^2 (r, theta, phi)=0 implies Psi (r, theta, phi)=0 If the radial wave function is equal to zero we get radial node and if angular part is equal to zero we get angular nodes. Total no. of nodes for any orbital = n - 1. Where ‘n’ is principal quantum number. The d-orbital with two nodal surfaces formed cones
01:19View SolutionWhen Schrodinger wave equation in polar coordinates is solved the solution for Φ is of the form Ψ(r,θ,ϕ)=R(r),Y(θ,ϕ). Here R(r) is radial part of wave function and Y(θ,ϕ) is angular part of the wave function. The region or space where probability of finding electron is zero is called nodal surface. If the probability of finding electron is zero then Ψ2(r,θ,ϕ)=0⇒Ψ(r,θ,ϕ)=0
If the radial wave function is equal to zero we get radial node and if angular part is equal to zero we get angular nodes. Total no. of nodes for any orbital = n - 1. Where ‘n’ is principal quantum number.
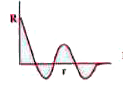represents 03:56View SolutionWhen Schrodinger wave equation in polar coordinates is solved the solution for Φ is of the form Ψ(r,θ,ϕ)=R(r),Y(θ,ϕ). Here R(r) is radial part of wave function and Y(θ,ϕ) is angular part of the wave function. The region or space where probability of finding electron is zero is called nodal surface. If the probability of finding electron is zero then Ψ2(r,θ,ϕ)=0⇒Ψ(r,θ,ϕ)=0
If the radial wave function is equal to zero we get radial node and if angular part is equal to zero we get angular nodes. Total no. of nodes for any orbital = n - 1. Where ‘n’ is principal quantum number.
Number of radial nodes for 4f orbital01:17View SolutionPsi^2 (r , theta , phi) represents (for schrodinger wave mechanical model)
01:07:45View SolutionIn the schrodinger wave equation, psi represents______.
05:03View SolutionIn Schrodinger 's wave equation , the symbol Ψ represents the
02:07View SolutionQuantum Mechanical Model and Schrodinger Wave Equation||Wave Function for Atomic Orbitals and their Graphs||Radial Probability Distribution Function and Graph
02:17View SolutionIf a=cosθ+isinθ, b=cosϕ+isinϕ, c=cosψ+isinψ and ab+bc+ca=2 then sin(θ−ϕ)+sin(ϕ−ψ)+sin(ψ−θ) equals
02:26View Solution