The average (mean) life of a radio nuclide which decays by parallel path is
Aλ1−−→B : λ1=1.8×10−2sec−1
2Aλ2−−→B , λ2=10−3sec−1
a) 52.63sec
b) 500sec
c) 50sec
d) none of these Solution in Punjabi
52.63sec
500sec
50sec
none of these
The correct Answer is:C
Step by step video & image solution for The average (mean) life of a radio nuclide which decays by parallel path is Aoverset(lambda_(1))(rarr)B : lambda_(1)=1.8xx10^(-2)sec^(-1) 2Aoverset(lambda_(2))(rarr)B , lambda_(2)=10^(-3)sec^(-1) a) 52.63 sec b) 500 sec c) 50 sec d) none of these by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 2 (Q.33 To Q.35)2videos
CHEMICAL KINETIC & NUCLEAR CHEMISTRY
- BOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 3 - Passage1videos
CHEMICAL KINETIC & NUCLEAR CHEMISTRY
- BOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 21videos
CHEMICAL KINETIC & NUCLEAR CHEMISTRY
- BOOK - NARENDRA AWASTHICHAPTER - SURFACE CHEMISTRYEXERCISE - Level -21videos
SURFACE CHEMISTRY
Similar Questions
In a sample of wood, the reading of a counter is 32 dpm and in a fresh sample of tree it is 122dpm . Due to error counter gives the reading 2 dpm in absence of .14C . Half life of .14C is 5770 years .
The approximate age (in years) of wood sample is :09:23View SolutionTwo consecutive irreversible first order reactions can be represented by
Ak1−−→Bk2−−→C
The rate equation for A is readily interated to obtain
[A]t=[A]0.e−k1t , and [B]t=k1[A]0k2−k1[e−k1(t)−e−k2(t)]
When k1=1s−1 and k2=500s−1 , select most appropriate graph
a)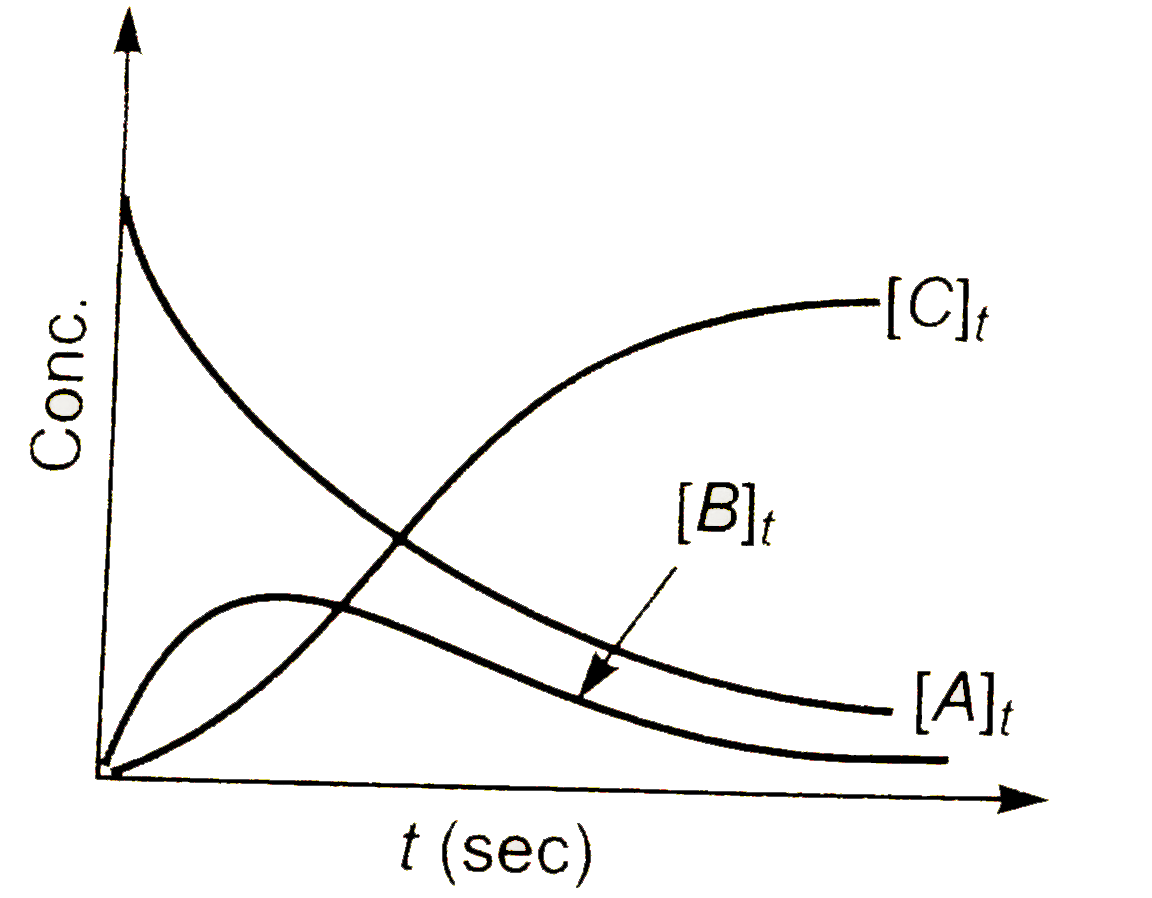 b)
b) 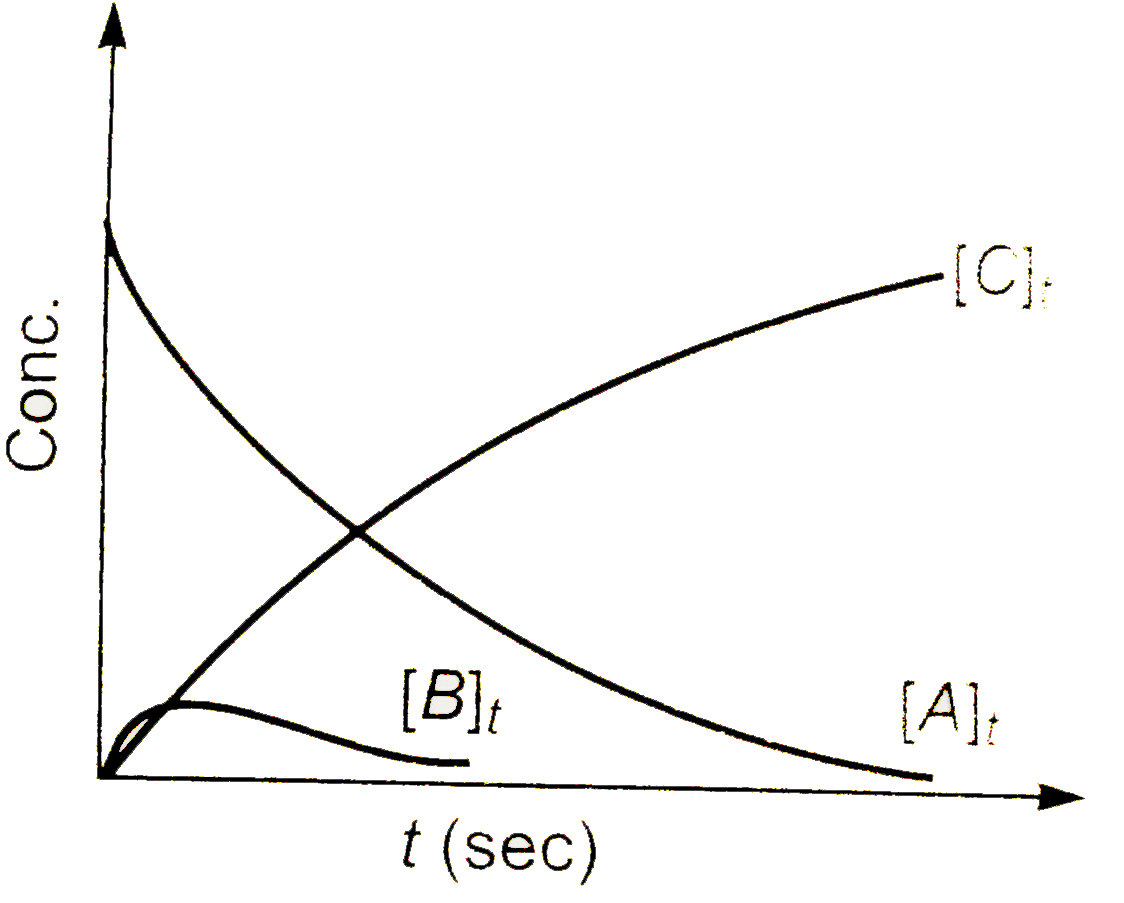
c)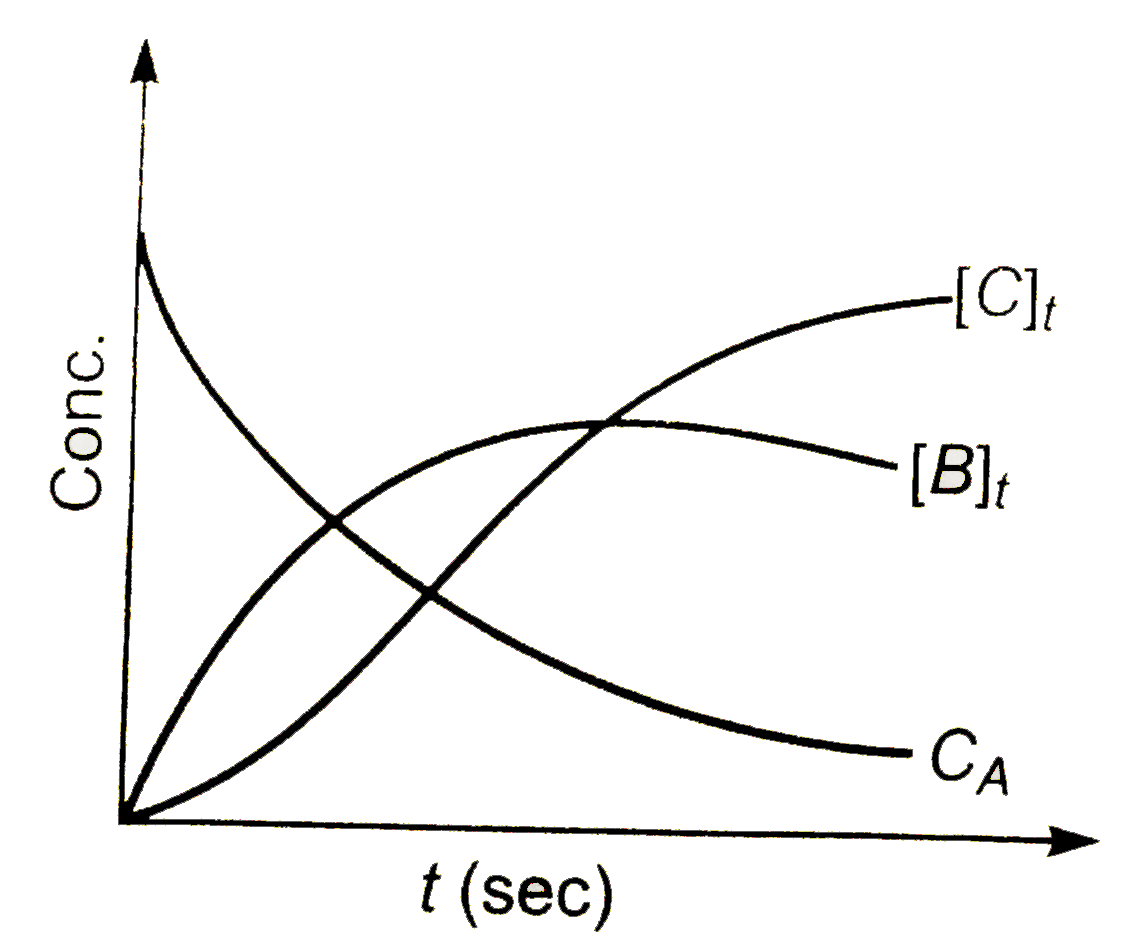 d)
d) 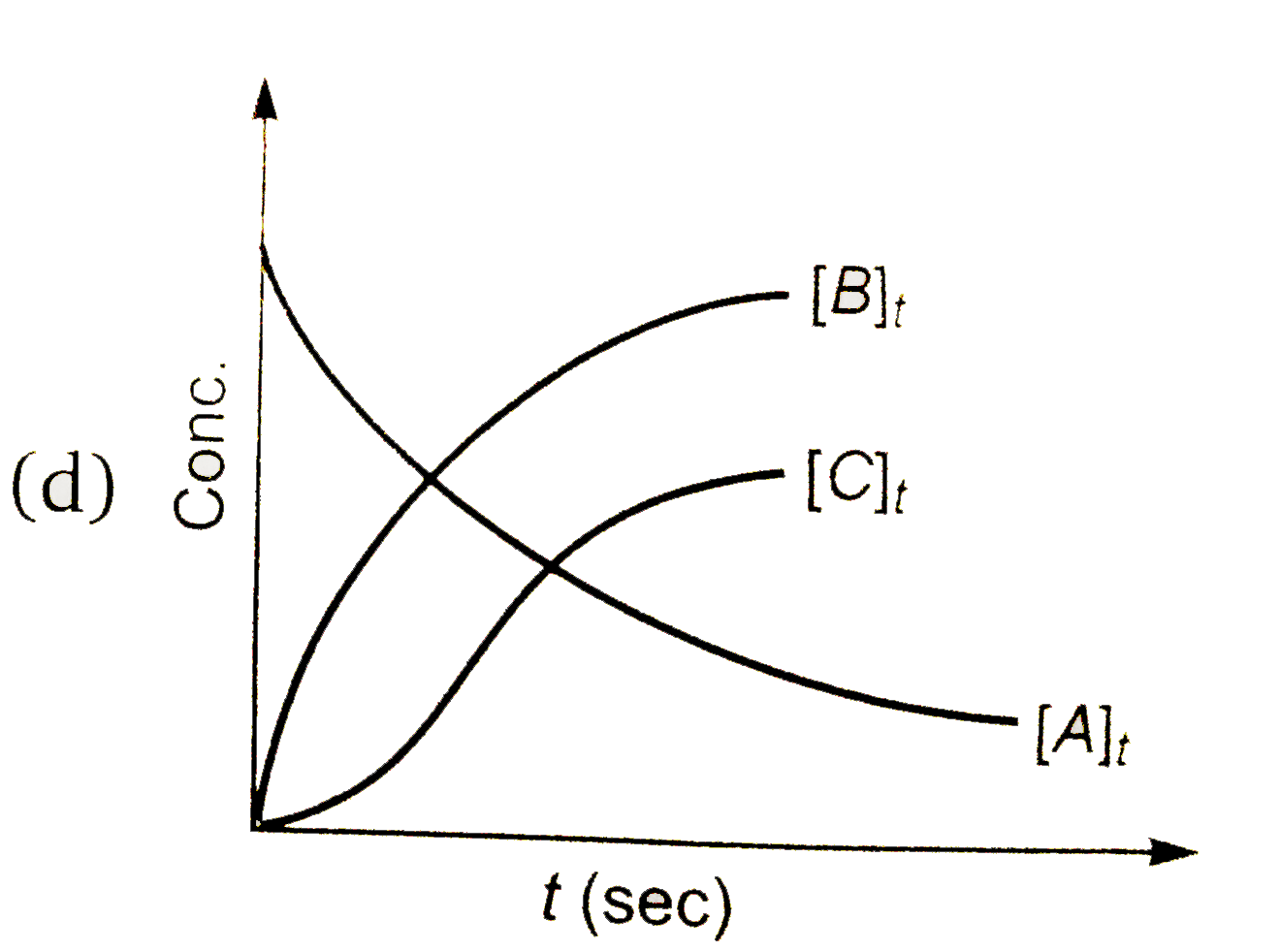 04:34View Solution
04:34View SolutionThe forward rate constant for the elementary reversible gaseous reaction
C2H6<⇒2CH3is1.57×10−3s−1at100K
What is the rate constant for the backward reaction at this temperature if 10−4 moles of CH3 and 10 moles of C2H6 are present in a 10 litre vessel at equilibrium .
a) 1.57×109Lmole−1s−1
b) 1.57×1010Lmole−1s−1
c) 1.57×1011Lmole−1s−1
d) 1.57×107Lmole−1s−1View Solutionfor the graph below, select correct order of temperture ?
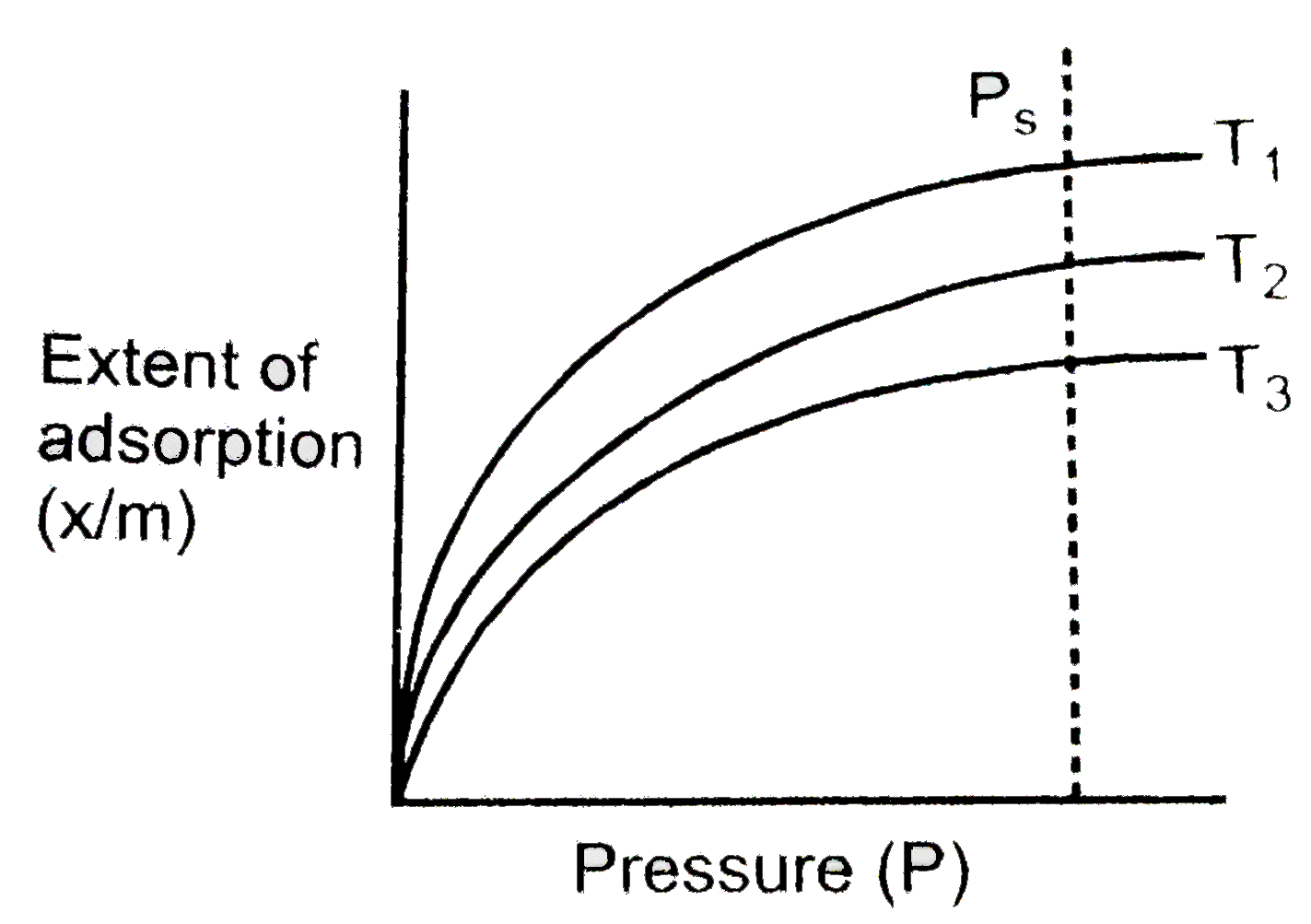 04:12View Solution
04:12View SolutionIf tan 82(1)/(2^(@))=sqrt(lambda_(1))+sqrt(lambda_(2))+sqrt(lambda_(3))+2 then lambda_(1)+lambda_(2)+lambda_(3) is equal to
02:13View SolutionTwo particle are moving perpendicular to each with de-Broglie wave length lambda_(1) and lambda_(2) . If they collide and stick then the de-Broglie wave length of system after collision is : (A) lambda = (lambda_(1) lambda_(2))/(sqrt(lambda_(1)^(2) + lambda_(2)^(2))) (B) lambda = (lambda_(1))/(sqrt(lambda_(1)^(2) + lambda_(2)^(2))) (C) lambda = (sqrt(lambda_(1)^(2) + lambda_(2)^(2)))/(lambda_(2)) (D) lambda = (lambda_(1) lambda_(2))/(sqrt(lambda_(1) + lambda_(2)))
06:09View SolutionThe average (mean) life of a radio nuclide which decays by parallel path is
Aλ1−−→B : λ1=1.8×10−2sec−1
2Aλ2−−→B , λ2=10−3sec−1View SolutionConsider a nuclear reaction : Aoverset(lambda_(1))rarrB+C and Boverset(lambda_(2))rarrC A converts into B and to C with decay with decay constant lambda_(1) B is alos stable nucleus which futher decays into stable nucleus C with decay constant lambda_(2). Mark the correct statement(s)
View SolutionA radioacive element decays by parallel path as given below: A overset(lambda_(1))(to) lambda_(1) = 1.8 xx 10^(-2) sec^(-1) 2A overset(lambda_(2))(to) B lambda_(2) = 10^(-3) sec^(-1) Average life of radio nuclide A will be:
00:56View SolutionIf the matrix A=⎡⎢ ⎢⎣λ21λ1λ2λ1λ3λ2λ1λ22λ2λ3λ3λ1λ3λ2λ23⎤⎥ ⎥⎦ is idempotent,
the value of λ21+λ22+λ23 is03:09View SolutionThe average (mean) life at a radio nuclide which decays by parallel path is : A overset(lambda_(1))rarr B, lambda_(1)=1.8 xx10^(-2)"sec"^(-1) 2A overset(lambda_(2))rarrC, lambda_(2)=10^(-3)"sec"^(-1)
05:22View SolutionA radioactive element decays by following three different parallel paths : A overset(lambda_(1))(to) B, lambda_(1) = 5 xx 10^(-2) sec^(-1) 2A overset(lambda_(2))(to) C,lambda_(2) = 3xx10^(-2) sec^(-1) 3A overset(lambda_(3))(to) D, lambda_(3) = 5xx10^(-3) sec^(-1) Calculate average life- time of element (in sec.) [lambda_(1), lambda_(2), lambda_(3) "are decay constans for respective reactions"]
01:52View SolutionThe average (mean) life of a radio nuclide which decays by parallel path is Aoverset(lambda_(1))(rarr)B : lambda_(1)=1.8xx10^(-2)sec^(-1) 2Aoverset(lambda_(2))(rarr)B , lambda_(2)=10^(-3)sec^(-1)
02:45View SolutionTwo particle are moving perpendicular to each with de-Broglie wave length lambda_(1) and lambda_(2) . If they collide and stick then the de-Broglie wave length of system after collision is : (A) lambda = (lambda_(1) lambda_(2))/(sqrt(lambda_(1)^(2) + lambda_(2)^(2))) (B) lambda = (lambda_(1))/(sqrt(lambda_(1)^(2) + lambda_(2)^(2))) (C) lambda = (sqrt(lambda_(1)^(2) + lambda_(2)^(2)))/(lambda_(2)) (D) lambda = (lambda_(1) lambda_(2))/(sqrt(lambda_(1) + lambda_(2)))
05:10View Solution→a=2ˆi+λ1ˆj+3ˆk,→b=4ˆi+(3−λ2)ˆj+6ˆk and →c=3ˆi+6ˆj+(λ3−1)ˆk are three vectors. Vector →b=2→a and →a is perpendicular to →b then the possible value of (λ1,λ2,λ3) is ..............
04:42View Solution

