The average velocity of CO2 at the temperature T1 Kelvin and the most probable veloctiy at T2 Kelvin is 9.0×104cms−1. Calculate the values of T1 and T2.
We know
Average speed uAV=√(8RTπM)
Most probable speed uMP=uMP=√(8RTM)
Average speed at T1K=MP speed at T2K for CO2
√(8RT1πM)=√(2RT2M)
T1T2=π4
Also for CO2,uMP=√(2RT2M)=9×104
∴
⎷(2×8.314×107×T244)=9×104
T2=2143.37K
∴ By eq (1) T1=1684.0K .
Topper's Solved these Questions
- BOOK - P BAHADURCHAPTER - GASEOUS STATEEXERCISE - Exercise B1videos
GASEOUS STATE
- BOOK - P BAHADURCHAPTER - GASEOUS STATEEXERCISE - Exercise 41videos
GASEOUS STATE
- BOOK - P BAHADURCHAPTER - GASEOUS STATEEXERCISE - Exercise 31videos
GASEOUS STATE
- BOOK - P BAHADURCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Exercise134videos
CHEMICAL EQUILIBRIUM
- BOOK - P BAHADURCHAPTER - IONIC EQUILIBRIUMEXERCISE - Exercise85videos
IONIC EQUILIBRIUM
Similar Questions
The average velocity of CO2 at the temperature T1K and maximum (most) proable velocity of CO2 at the temperature T2K is 9×104cms−1. Calculate the values of T1 and T2.
View SolutionThe average speed at T1K and the most probable speed at T2K of CO2 gas is 9×104cms−1. Calculate the value of T1 and T2.
View Solution
Knowledge Check
- Question 1 - Select One
The average velocity of CO2 at T K is 9×104cms−1. The value of T is
A1682.5KB2143.37C373.20KD1240 K - Question 2 - Select One
The rms velocity of CO2 at temperature T(in Kelvin) is x cm s−1. At what temperature (in Kelvin) would the rms velocity of nitrous oxide be 4xcms−1?
A16TB2TC4TD32T - Question 3 - Select One
The r.m.s velocity of CO2 at a temperature T in Kelvin) is xcm sec−1 . At what temperature (in Kelvin), the r.m.s. velocity of nitrous oxide would be 4x cm sec−1?
A16TB2TC4TD32T
The average velocity of CO2 at T1 K and most probable velocity at T2K is 9×104cm/s. Calculate the values of temperatures, T1 and T2K.
View Solution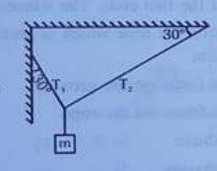
Calculate T1&T2.View Solution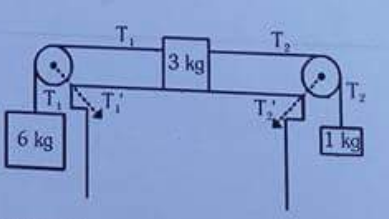
Calculate a, T1,T2,T1'&T2'.View SolutionThe velocity of sound waves in an ideal gas at temperatures T1KandT2 are respectively v1andv2 . The rms velocity of gas molecules at these two temperatures are w1ande2 , respectively then
View SolutionThe figure shows the variation of V with i at temperatures T1 and T2. Then T1−T2 is proportional to
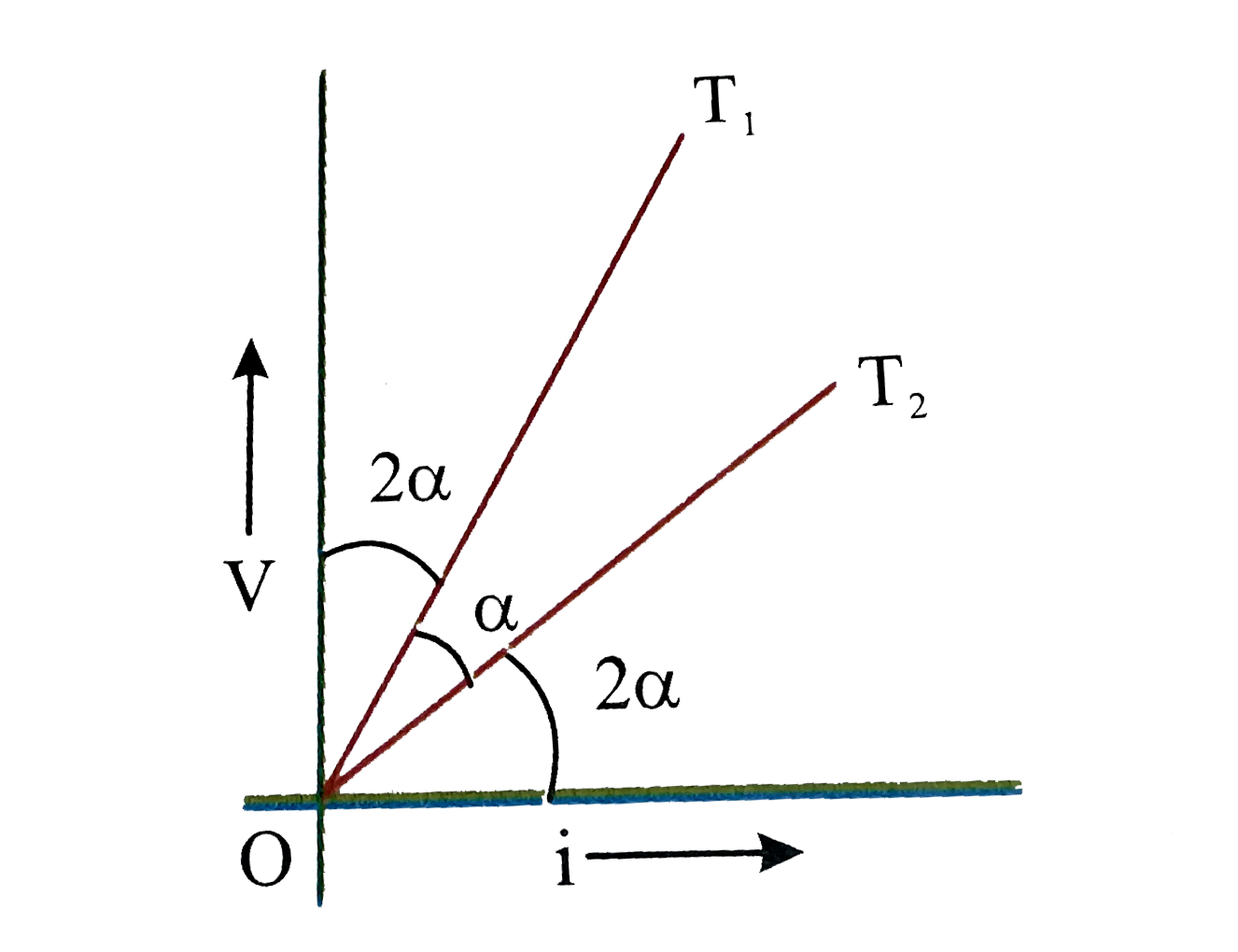 View Solution
View Solution

