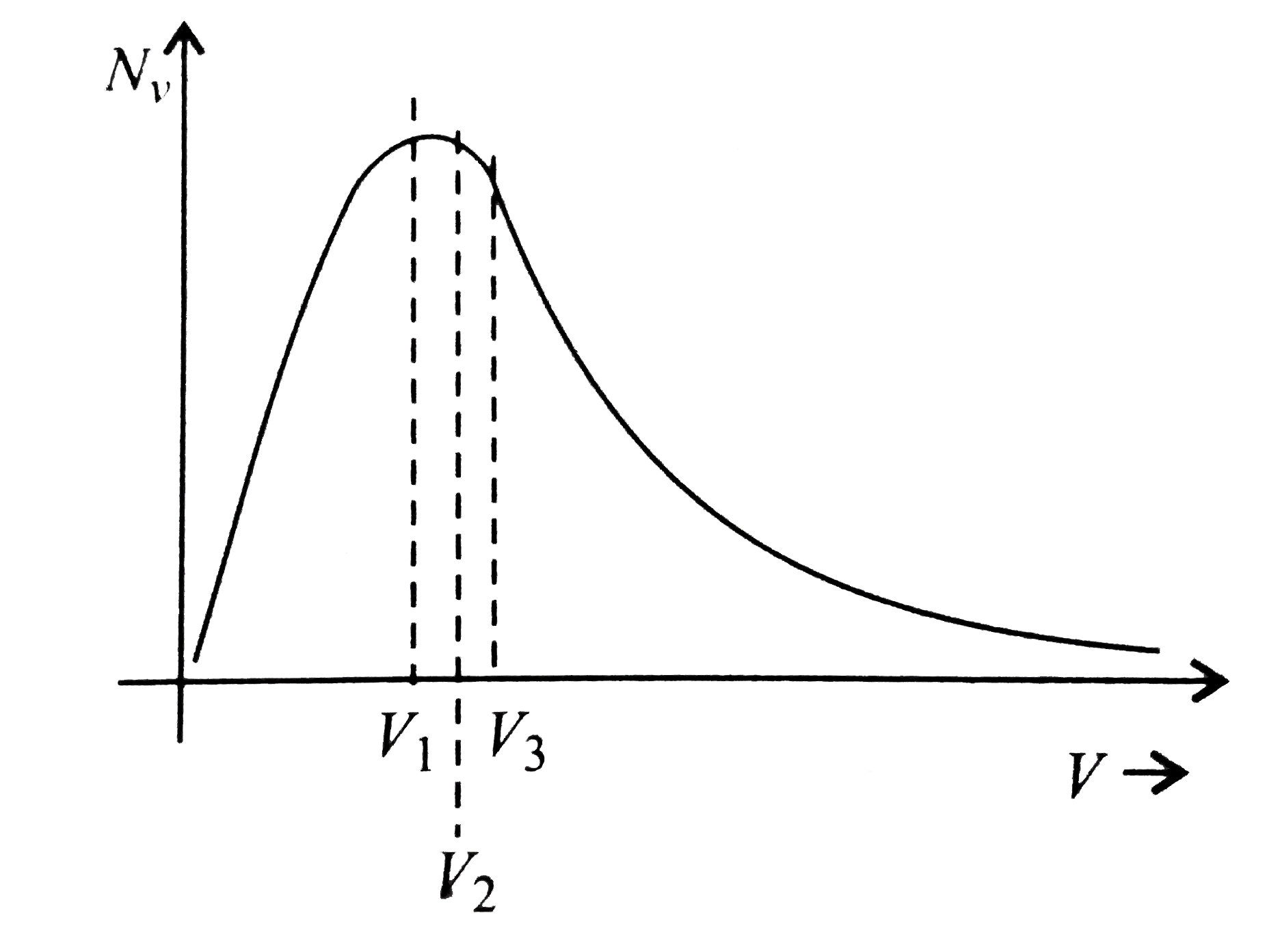
The distribution of the molecular velocities of gas molecules at any temperature $T$ is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)

where
$v$ is molecular velocity
$n$ is number of molecules having velocity $v$
Let us define $Δ N_{v}$ , which is equal to the number of molecules between the velocity range $v$ and $v + Δ v$ , given by
$Δ N_{v} = 4 π N a^{3} e^{- b v^{2}} v^{2} Δ v$
where
$N$ is total number of molecules
$a = \sqrt{\frac{M_{0}}{2 π R T}}$ and $b = \frac{M_{0}}{2 R T}$
$R$ is universal gas constant
$T$ is temperature of the gas
$M_{0}$ is molecular weight of the gas
Answer the following question:
$S I$ units of $a$ are

A

$M^{3}$

B

$m^{- 1} s$

C

$m^{2} s^{- 2}$

D

$m s^{2}$

Text Solution

Verified by Experts

$m^{- 1} s$

|

Updated on:21/07/2023

Class 11 CHEMISTRY STATES OF MATTER

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The distribution of the molecular velocities of gas molecules at any temperature $T$ is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)

where
$v$ is molecular velocity
$n$ is number of molecules having velocity $v$
Let us define $Δ N_{v}$ , which is equal to the number of molecules between the velocity range $v$ and $v + Δ v$ , given by
$Δ N_{v} = 4 π N a^{3} e^{- b v^{2}} v^{2} Δ v$
where
$N$ is total number of molecules
$a = \sqrt{\frac{M_{0}}{2 π R T}}$ and $b = \frac{M_{0}}{2 R T}$
$R$ is universal gas constant
$T$ is temperature of the gas
$M_{0}$ is molecular weight of the gas
Answer the following question:
If $\frac{P}{P_{c}} = P_{r}$ , $\frac{T}{T_{c}} = T_{r}$ , and $\frac{V_{m}}{V_{m, c}} = V_{r}$ where
A $P_{r}$ ia reduced pressure, $P_{c}$ is critical pressure
B $T_{r}$ ia reduced temperature, $T_{c}$ is critical temperature
C $V_{r}$ is reduced volume, $V_{c}$ is critical volume
Dthen the temperature of state (or van der Waals equation), only in terms of $P_{r}$ , $T_{r}$ , and $V_{r}$ is
Question 2 - Select One
The root mean square velocity of a gas molecule at any temperature T K of a gas molecule of molecular weight M is
A $\sqrt{8 R T / M}$
B $\sqrt{2 R T / M}$
C $\sqrt{3 R T / M}$
Dzero
Question 3 - Select One
The velocity of molecules of a gas at temperature 120 K is v. At what temperature will the velocity be 2v?
A120 K
B240 K
C480 K
D1120 K

CENGAGE CHEMISTRY-STATES OF MATTER-Exercises (Linked Comprehensive)

Home
Ask Doubt
Profile