In maxwell's speed distribution curve, for N2 gas, the average of |relative velocity| between two molecules at 300 k will be : -
300 m/sec
610 m/sec
920 m/sec
zero
The correct Answer is:B
To find the average relative velocity between two nitrogen (N₂) gas molecules at 300 K using Maxwell's speed distribution, we can follow these steps:
1. Understanding Relative Velocity:
The relative velocity |vrel| between two molecules can be expressed as:
|vrel|=√v21+v22−2v1v2cosθ
where v1 and v2 are the speeds of the two molecules and θ is the angle between their velocity vectors.
2. Assuming Equal Speeds:
For simplicity, we assume both molecules have the same speed v. Thus, the expression simplifies to:
|vrel|=√2v2(1−cosθ)=v√2(1−cosθ)
3. Using Trigonometric Identity:
We can use the identity 1−cosθ=2sin2(θ/2):
|vrel|=v√2⋅2sin2(θ/2)=2v|sin(θ/2)|
4. Finding the Average Relative Velocity:
To find the average of the relative velocity, we integrate over the angle θ from 0 to π:
⟨|vrel|⟩=1∫π0dθ∫π02v|sin(θ/2)|dθ
5. Calculating the Integral:
The integral can be computed as follows:
∫π0|sin(θ/2)|dθ=2∫π/20sin(θ/2)dθ=2⋅2=4
Thus, the average relative velocity becomes:
⟨|vrel|⟩=4vπ
6. Relating Speed to Temperature:
The average speed v of a gas molecule can be expressed in terms of the temperature T and the molar mass M:
v=√8RTπM
where R is the universal gas constant.
7. Substituting Values:
For nitrogen (N₂), the molar mass M is 28 g/mol or 28×10−3 kg/mol. At T=300 K:
v=√8×8.314×300π×0.028≈478.6 m/s
8. Final Calculation:
Now substituting back into the average relative velocity equation:
⟨|vrel|⟩=4⋅478.6π≈606 m/s
Conclusion:
The average relative velocity between two nitrogen molecules at 300 K is approximately 606 m/s, which is closest to the option 610 m/s.
The relative velocity |vrel| between two molecules can be expressed as:
|vrel|=√v21+v22−2v1v2cosθ
where v1 and v2 are the speeds of the two molecules and θ is the angle between their velocity vectors.
For simplicity, we assume both molecules have the same speed v. Thus, the expression simplifies to:
|vrel|=√2v2(1−cosθ)=v√2(1−cosθ)
We can use the identity 1−cosθ=2sin2(θ/2):
|vrel|=v√2⋅2sin2(θ/2)=2v|sin(θ/2)|
To find the average of the relative velocity, we integrate over the angle θ from 0 to π:
⟨|vrel|⟩=1∫π0dθ∫π02v|sin(θ/2)|dθ
The integral can be computed as follows:
∫π0|sin(θ/2)|dθ=2∫π/20sin(θ/2)dθ=2⋅2=4
Thus, the average relative velocity becomes:
⟨|vrel|⟩=4vπ
The average speed v of a gas molecule can be expressed in terms of the temperature T and the molar mass M:
v=√8RTπM
where R is the universal gas constant.
For nitrogen (N₂), the molar mass M is 28 g/mol or 28×10−3 kg/mol. At T=300 K:
v=√8×8.314×300π×0.028≈478.6 m/s
Now substituting back into the average relative velocity equation:
⟨|vrel|⟩=4⋅478.6π≈606 m/s
The average relative velocity between two nitrogen molecules at 300 K is approximately 606 m/s, which is closest to the option 610 m/s.
Similar Questions
A large number of particles are moving each with speed v having directions of motion randomly distributed. What is the average relative velocity between any two particles averaged over all the pairs?
View SolutionThe average velocity of the molecules in a gas in equilibrium is
View SolutionConsider a collection of a large number of particles each with speed v. The direction of velocity is randomly distributed in the collection. Show that the magnitude of the relative velocity between a pair of particles averaged over all the pairs in the collection is greater than v.
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)
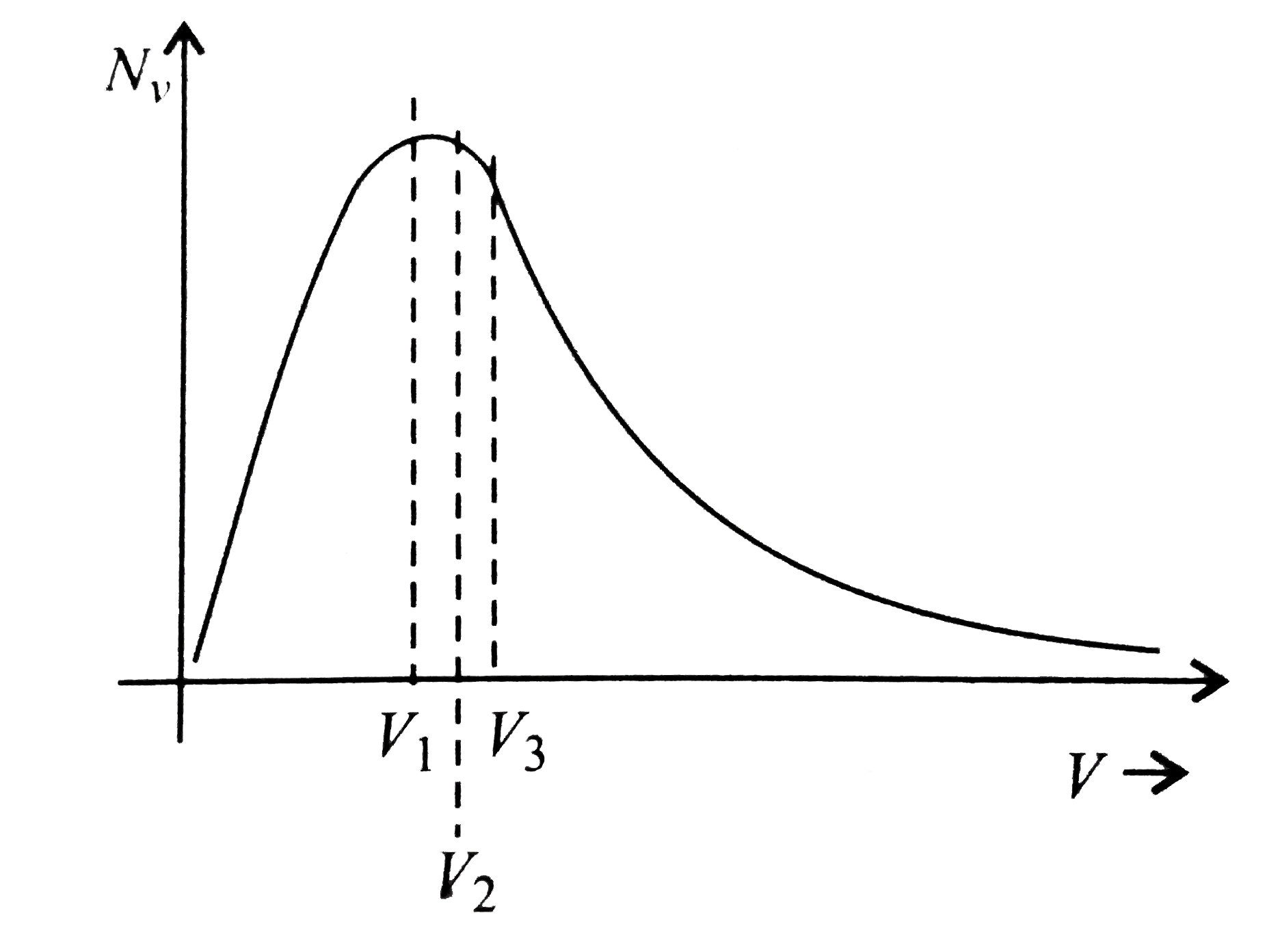
where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
SI units of a are
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)
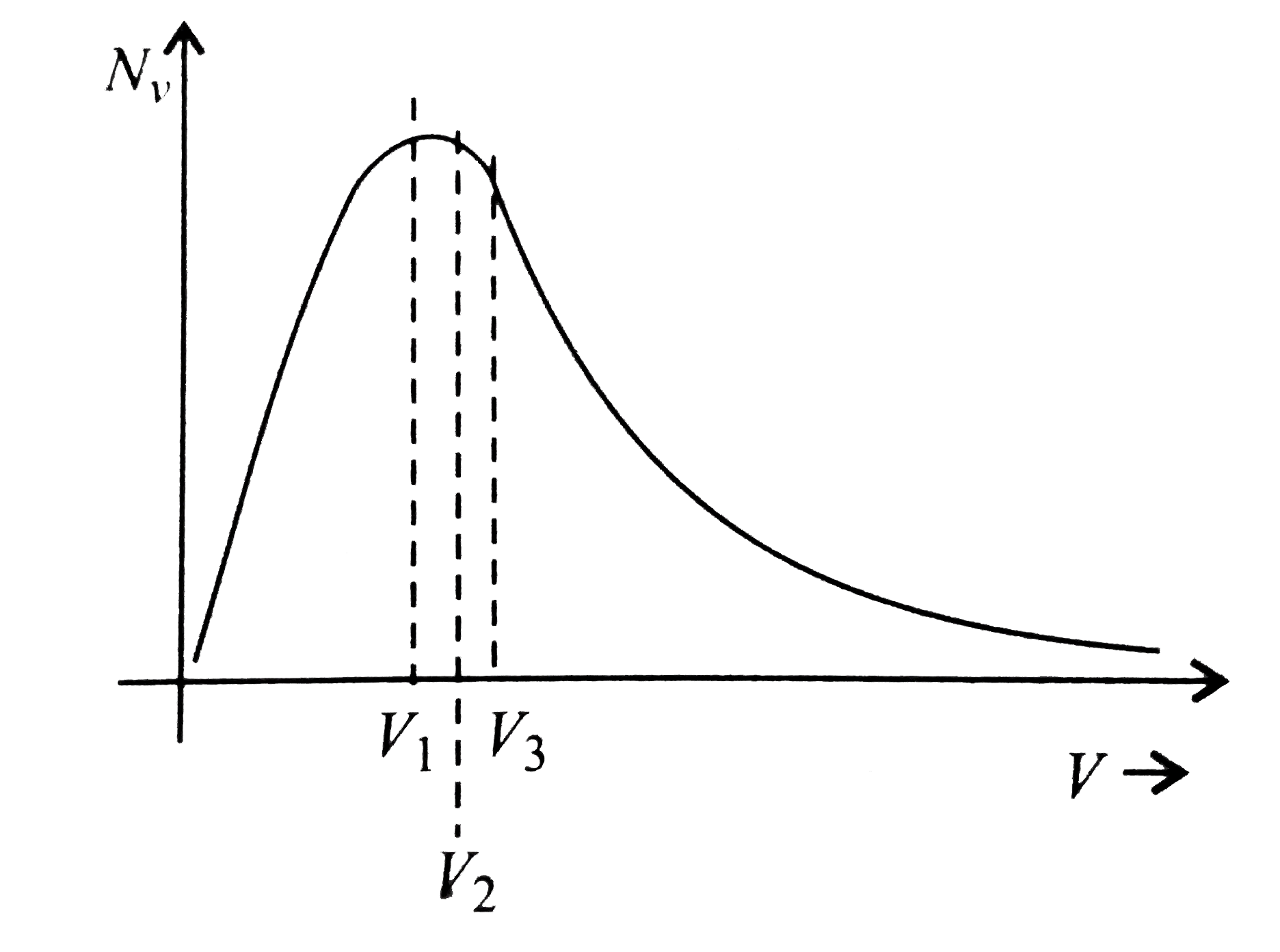
where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
SI units of b are
View SolutionThe temperature in kelvin at which the average speed of H2 molecues will be same as that of N2 molecules at 35 C will be ?
View SolutionAt what temperature would N2 molecules have same average speed as CO molecules at 200 K.
View SolutionStatement-1 :The area under the maxwell distribution molecular speed curve remains same irrespective of temperature of gas.
Statement-2 :The fraction of molecules with most probable speed increases with increases of temperature.
View SolutionAt what temperature do the average speed of CH4(g) molecules equal the average speed of O2 molecules at 300 K ?
View SolutionWhich expression gives average speed of gas molecules?
View Solution
