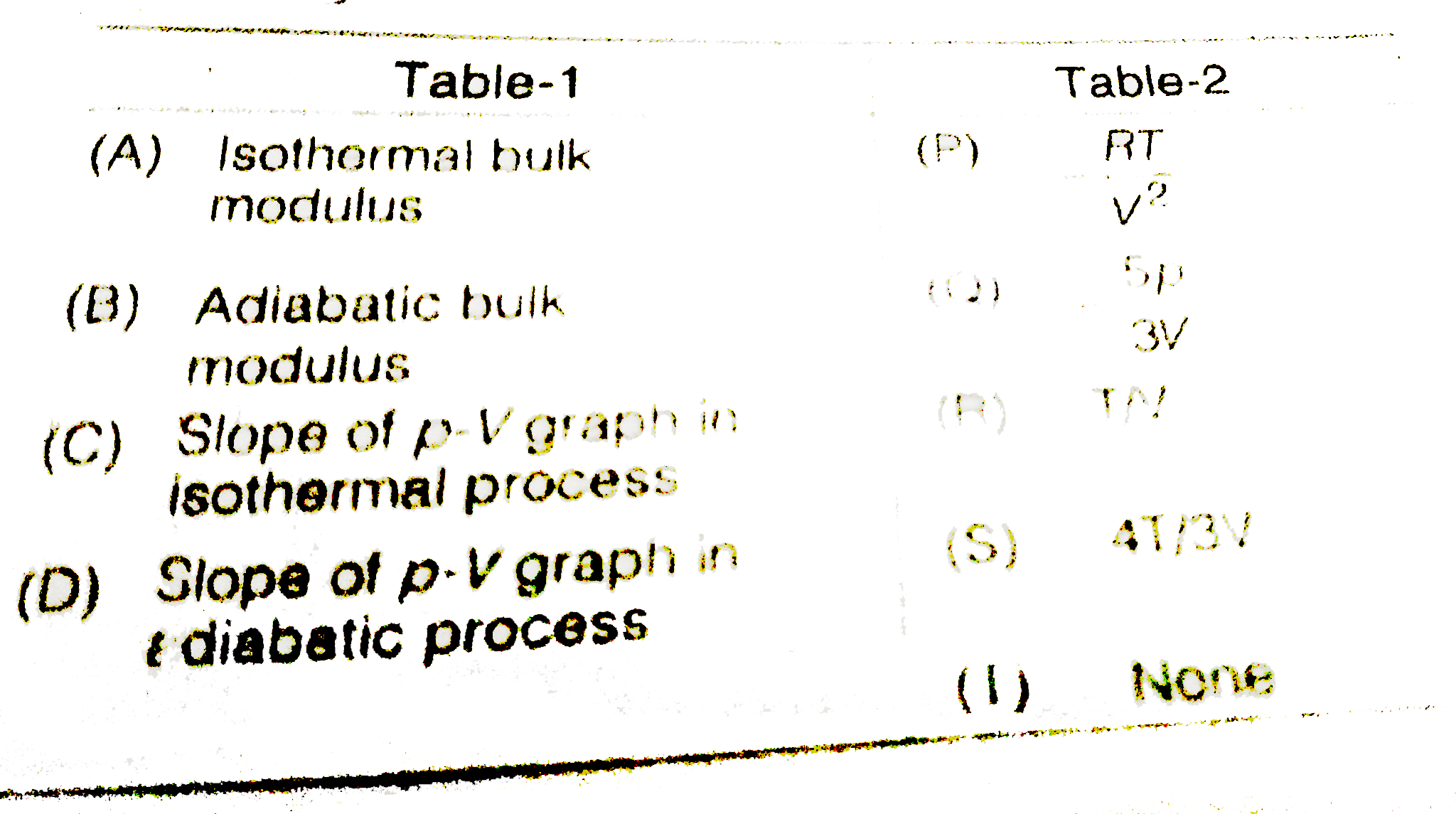The enthalpy of a monoatomic gas at T kelvin is
A
72RT
B
32RT
C
12RT
D
52RT
Text Solution
The correct Answer is:D
Enthalpy of monoatmic gas at T kelvin is =52RT.
|
Topper's Solved these Questions
- CHEMICAL THERMODYNAMICS AND ENERGETICBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - CHEMICAL THERMODYNAMICS AND ENERGETICEXERCISE - MHT CET Corner
40 Videos
- CHEMICAL THERMODYNAMICS AND ENERGETICBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - CHEMICAL THERMODYNAMICS AND ENERGETICEXERCISE - Exercise 1
88 Videos
- CHEMICAL KINETICS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - CHEMICAL KINETICS EXERCISE - MHT CET CORNER
20 Videos
- CHEMISTRY IN EVERYDAY LIFE BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - CHEMISTRY IN EVERYDAY LIFE EXERCISE - MHT CET CORNER
11 Videos
Similar Questions
Knowledge Check
A monoatomic gas lighter than air is
AheliumBnitrogenChydrogenDneonIf the thermal energy of a monoatomic gas molecules of mass m at temperature T kelvin is of the order of f/2kT, then the deBroglie wavelength of the matter waves is of the order of
A2h/3kTBh/2mkTCh/√3mkTD√h/2mkTWhen one mole of a monoatomic ideal gas at initial temperature T K expands adiabatically from 1 litre to 2litres , the final temperature in Kelvin would be
ATBT22/3CT−23×0.0821DT+23×0.0821
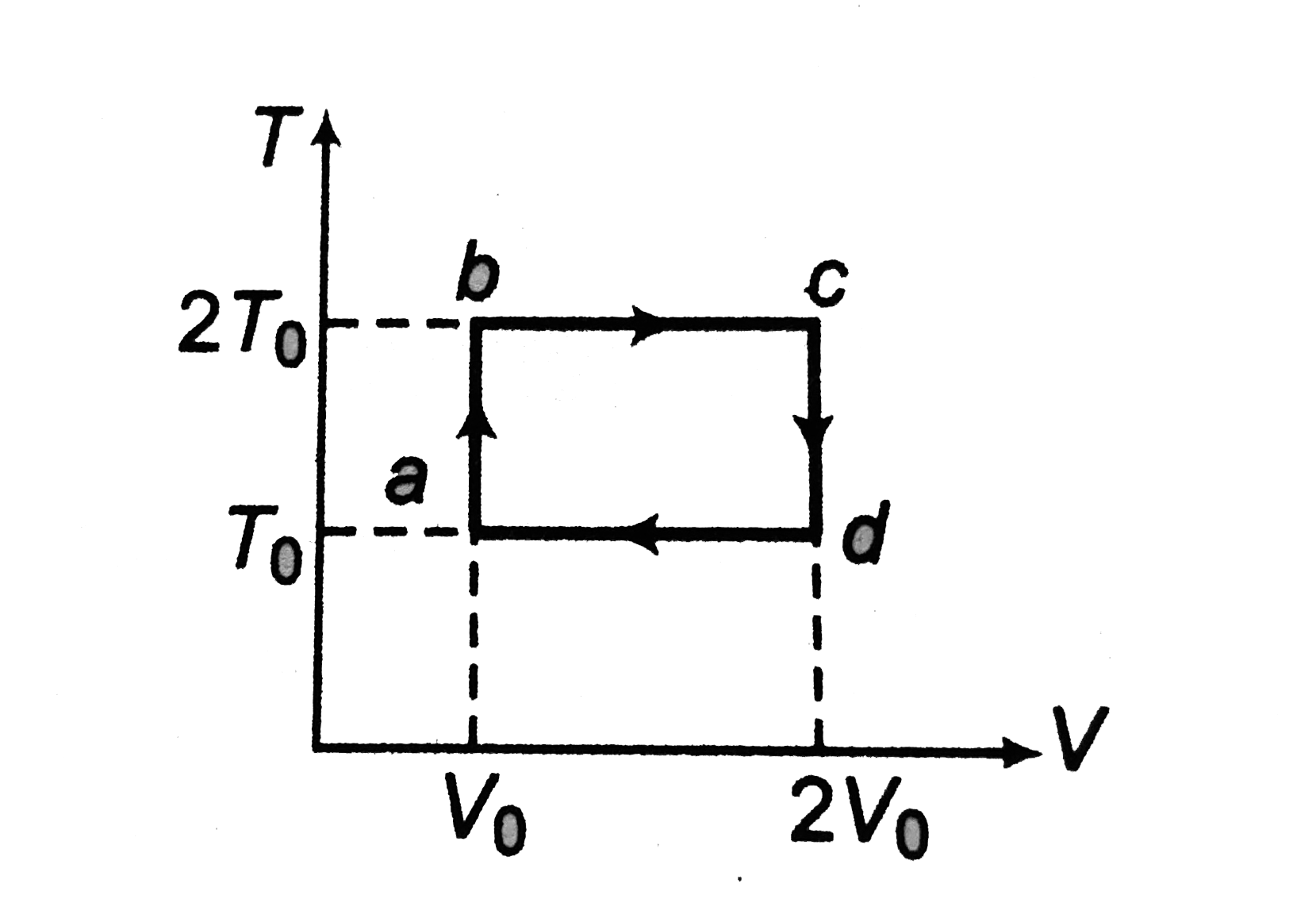
T-V diagram of two moles of a monoatomic gas is as shown in figure.
For the process abcda choose the correct options given below
View SolutionFind the molar specific heat of the process p=aT for a monoatomic gas, a being constant.
View SolutionEnthalpy of 1 mole monoatomic ideal gas is equals to :-
View SolutionWhen one mole of monoatomic ideal gas at T temperature undergoes adiabatic change under a constant external pressure of 1 atm, change in volume is from 1 L to 2L. The final temperature in kelvin would be
View SolutionWhen 1mol of a monoatomic ideal gas at TK undergoes adiabatic change under a constant external pressure of 1atm, changes volume from 1L→2L. The final temperature (in K) would be
View Solution