The following data were obtained during the first thermal decompoistion of N2O5(g) at constant volume.
2N2O5(g)→2N2O4(g)+O2(g)
∣∣
∣
∣∣S.No.Time (s)Total pressure (atm)i.00.5ii.1000.512∣∣
∣
∣∣
Calculate the rate constant.
2N2O5(g)→2N2O4(g)+O2(g).
Att=00.5atm0atm0atmAt time t(0.5−2x)2xatmxatm
Let the pressure of N2O5(g) decreases by 2x atm. As two moles of N2O5(g) decompose to give two moles of N2O4(g) and one mole of O2(g), the pressure of N2O4(g) increases by 2x atm and that of O2(g) increases by x atm.
PT=PN2O5+PO2
=(0.5−2)+(2x)+(x)
=0.5+x
or x=PT−0.5
Partial pressure of N2O5 at any time 't' is Pt which is given as
Pt=.5−2x
Substituting the value of x, we get
Pt=0.5−2(PT−0.5)
=1.5−2PT
At time t=100 s, we have
PT=0.512atm
Thus Pt(N2O5=1.5−2(0.512)
=1.5−1.024
=0.476atm
Integrated rate law in term of pressures is
k=2.303tlog(P0)Pt
=2.303100slog(0.5atm)0.476atm
=2.303100s×0.0216
=4.98×10−4s−1
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - R SHARMACHAPTER - CHEMICAL KINETICSEXERCISE - Follow-up 1
8 Videos
- CHEMICAL KINETICSBOOK - R SHARMACHAPTER - CHEMICAL KINETICSEXERCISE - Follow-up 2
10 Videos
- BIOMOLECULESBOOK - R SHARMACHAPTER - BIOMOLECULESEXERCISE - Archives
47 Videos
- CHEMISTRY IN EVERYDAY LIFEBOOK - R SHARMACHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - Archives
11 Videos
Similar Questions
The following data were obtained during the first order thermal decomposition of N2O5 (g) at constant volume:
2N2O5(g)→2N2O4(g)+O2(g)
(S.no,Time,Total Pressure / atm),(1,0,0,5),(2,100,0.512)
Calculate the rate constant.
View SolutionThe following data were obtained the first order thermal decomposition of N2O5(g) at constant volume : 2N2O5(g)→2N2O4(g)+O2(g)
S. No.Time/sTotal pressure (atm)100.521000.512
Calculate the rate constant.
View Solution
Knowledge Check
The following data were obtained during the first order thermal
decomposition of SO2Cl2 at a constant volume SO2Cl2(g)→SO2(g)+Cl2(g)
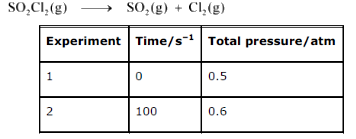
Calculate the rate of the reaction when total pressure is 0.65 atmA0.35atmS−1B2.235×10−3atmS−1C7.8×10−4atms−1D1.55×10−4atmS−1For the first order reaction
2N2O5(g)→4NO2(g)+O2(g)AThe concentration of the reactant decreases exponentially with time.BThe half life of the reaction decreases with increaisng temperature.CThe half life of the reaction depends on the initial concentration of the reactant.DThe reaction proceeds to 99.6% completion in 8 half. Life durations.For the first order reaction
2N2O5(g)→4NO2(g)+O2(g)AThe concentration of the reaction decreases exponentially with timeBThe half-life of the reaction decreases with increasing temperatureCThe half-life of the reaction depends on the initial concentration of the reactantDThe reaction proceeds to 99.6 % completion in eight half-life duration
The following data were obtained during the first order thermal decomposition of N2O5(g) at constant volume.
2N2O5(g)→2N2O2(g)+O2(g)

Calculate the rate constant for the gaseous reaction.
View SolutionThe following data were obtained during the first order thermal decomposition of N2O5 at constant volume :
2N2O5→2N2O4+O2

Calculate rate constant.
View SolutionThe following data were obtained during the first order thermal
decomposition of SO2Cl2 at a constant volume SO2Cl2(g)→SO2(g)+Cl2(g)

Calculate the rate of the reaction when total pressure is 0.65 atm
View SolutionThe following rate data were obtained for the thermal decomposition of N2O5(g)
2N2O5(g)→2N2O4(g)+O2(g)
Time (sec)050Total pressure (atm)0.20.25
Calculate the reaction rate when the total pressure is 0.28 atm
View SolutionFor the first order reaction
2N2O5(g)→4NO2(g)+O2(g)
View Solution
