The number of α-particles emitted per second by 1g of radium is 3.608×1010. Calculate decay constant and t12
To solve the problem, we will follow these steps:
Step 1: Understand the relationship between the decay constant and activity
The activity (A) of a radioactive substance is given by the formula:
A=−dNdt=λN
where:
- A is the activity (number of decays per second),
- λ is the decay constant,
- N is the number of radioactive nuclei present.
Step 2: Calculate the number of moles of radium in 1 gram
The molar mass of radium (Ra) is approximately 226 g/mol. Therefore, the number of moles in 1 gram of radium is:
Nmoles=1 g226 g/mol≈0.00442 moles
Step 3: Calculate the number of atoms (N) in 1 gram of radium
Using Avogadro's number (NA=6.022×1023 atoms/mol), we can find the total number of atoms:
N=Nmoles×NA=0.00442 moles×6.022×1023 atoms/mol
N≈2.66×1021 atoms
Step 4: Relate activity to decay constant
Given that the activity A is 3.608×1010 decays per second, we can substitute into the activity formula:
A=λN
3.608×1010=λ×2.66×1021
Step 5: Solve for the decay constant λ
Rearranging the equation gives:
λ=3.608×10102.66×1021
Calculating this gives:
λ≈1.36×10−11 s−1
Step 6: Calculate the half-life t1/2
The half-life is related to the decay constant by the formula:
t1/2=0.693λ
Substituting the value of λ:
t1/2=0.6931.36×10−11
Calculating this gives:
t1/2≈5.10×1010 seconds
Summary of Results
- Decay constant λ≈1.36×10−11 s−1
- Half-life t1/2≈5.10×1010 seconds
The activity (A) of a radioactive substance is given by the formula:
A=−dNdt=λN
where:
- A is the activity (number of decays per second),
- λ is the decay constant,
- N is the number of radioactive nuclei present.
The molar mass of radium (Ra) is approximately 226 g/mol. Therefore, the number of moles in 1 gram of radium is:
Nmoles=1 g226 g/mol≈0.00442 moles
Using Avogadro's number (NA=6.022×1023 atoms/mol), we can find the total number of atoms:
N=Nmoles×NA=0.00442 moles×6.022×1023 atoms/mol
N≈2.66×1021 atoms
Given that the activity A is 3.608×1010 decays per second, we can substitute into the activity formula:
A=λN
3.608×1010=λ×2.66×1021
Rearranging the equation gives:
λ=3.608×10102.66×1021
Calculating this gives:
λ≈1.36×10−11 s−1
The half-life is related to the decay constant by the formula:
t1/2=0.693λ
Substituting the value of λ:
t1/2=0.6931.36×10−11
Calculating this gives:
t1/2≈5.10×1010 seconds
- Decay constant λ≈1.36×10−11 s−1
- Half-life t1/2≈5.10×1010 seconds
Topper's Solved these Questions
- ATOMIC STRUCTURE AND RADIOACTIVITYBOOK - RC MUKHERJEECHAPTER - ATOMIC STRUCTURE AND RADIOACTIVITYEXERCISE - Objective Problems
66 Videos
- ATOMIC STRUCTURE AND RADIOACTIVITYBOOK - RC MUKHERJEECHAPTER - ATOMIC STRUCTURE AND RADIOACTIVITYEXERCISE - Objective Problems
66 Videos
- ATOMIC WEIGHTBOOK - RC MUKHERJEECHAPTER - ATOMIC WEIGHTEXERCISE - PROBLEMS
6 Videos
Similar Questions
The atomic weight of radius is 226. It is observed that 3.67×1010 α−particles are emitted per second from one gram of radium. Calculate in years the half period of radium.
View SolutionA 50 watt bulb emits monochromatic red light of wavelength of 795 nm. The number of photons emitted per second by the bulb is x×1020. The value of x is _______.
(Nearest integer)
[Given : h=6.63×10−34Jsandc=3.0×108ms−1]
View Solution
Knowledge Check
The number of α-particles emitted per second by 1g fo .226Ra is .7×1010. The decay constant is:
A1.39×10−11sec−1B13.9×10−11sec−1C139×10−10sec−1D13.9×10−10sec−1The number of α- particle emitted per second by 1 g of Ra-226 is 3.7×1010 . Find the decay constant
A1.39×10−11sec−1B13.9×10−11sec−1C3.7×10−11sec−1D2.78×10−11sec−1The number of α particles emitted per second by 1g of 88226 Ra is 3.7×1010. The decay constant is :
A1.39×10−11sec−1B13.9×10−11sec−1C139×10−10sec−1D13.9×10−10sec−1
A 50 watt bulb emits monochromatic red light of wavelength of 795 nm. The number of photons emitted per second by the bulb is x×1020. The value of x is _______.
(Nearest integer)
[Given : h=6.63×10−34Jsandc=3.0×108ms−1]
View SolutionHow many alpha particles are emitted per second by 1 microgram of radium
View SolutionPlutinium has atomic mass 210 and a decay constant equal to 5.8×10−8s−1. The number of α-particles emitted per second by 1mgplutonium is
(Avagadro's constant =6.0×1023).
View SolutionThe ground (Fig.) shows the number of particles Nt emitted per second by a radioactive source as a function of time t
The relationship between Nt and t is.
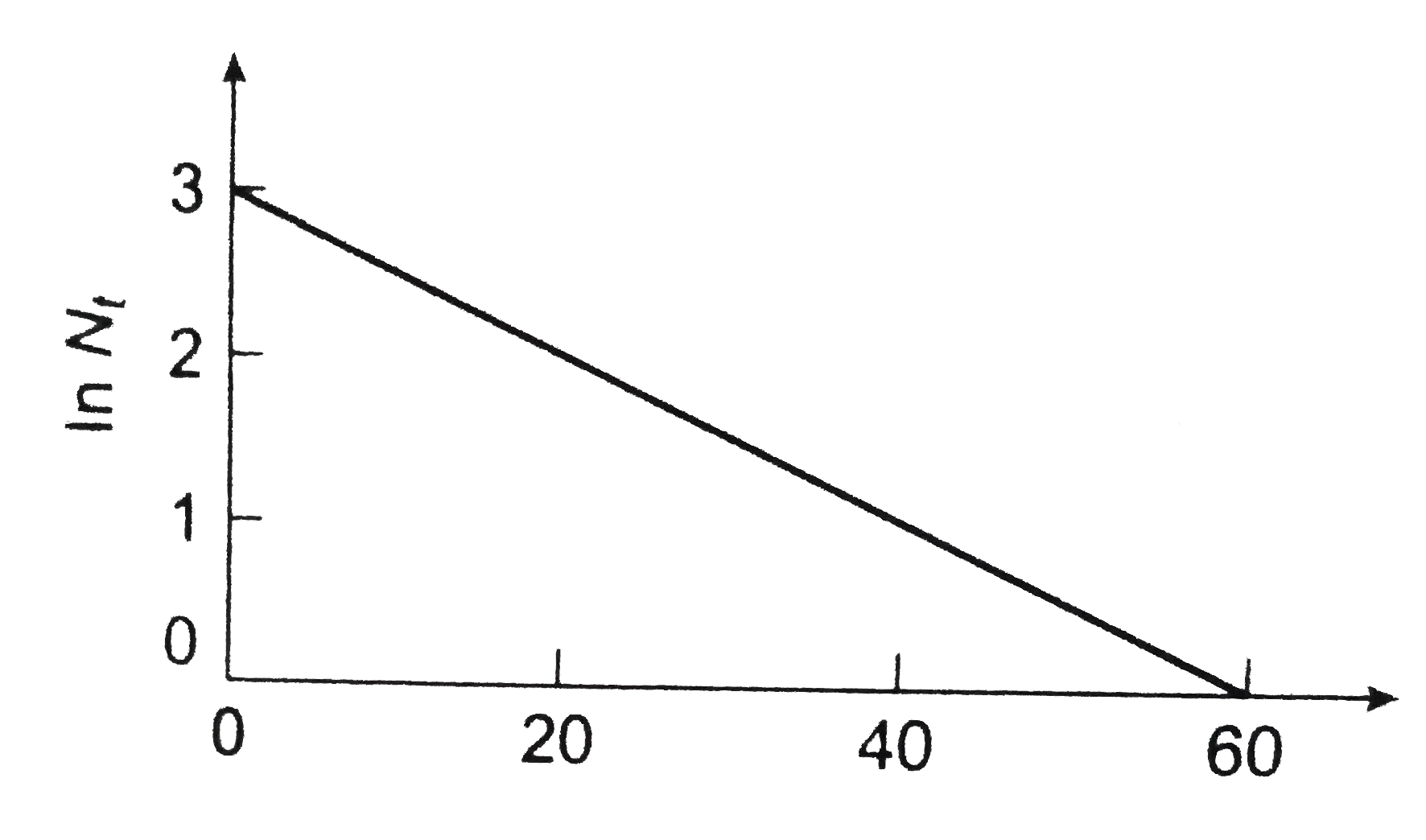 .
.
View SolutionNumber of α- particles emitted per second by a radioactive element falls to 1//32 of its original value in 50 days. The half-life-period of this element is
View Solution
