What is the work done when 1 mole of a gas expands isothermally from 25 L to 250 L at a constant pressure of 1 atm and a temperature of 300 K ?
(a) −3542J
(b) −5744J
(c) −2657J
(d) −4890J
The correct Answer is:B
To solve the problem of calculating the work done when 1 mole of a gas expands isothermally from 25 L to 250 L at a constant pressure of 1 atm and a temperature of 300 K, we can follow these steps:
Step 1: Identify the Given Data
- Number of moles (n) = 1 mole
- Initial volume (V_initial) = 25 L
- Final volume (V_final) = 250 L
- Constant pressure (P) = 1 atm
- Temperature (T) = 300 K
Step 2: Use the Formula for Work Done in Isothermal Expansion
For isothermal expansion of an ideal gas, the work done (W) can be calculated using the formula:
W=−2.303nRTlog(VfinalVinitial)
Step 3: Convert the Gas Constant to Appropriate Units
Since the pressure is given in atm and we want the work in joules, we will use the gas constant R=8.314J/(mol K).
Step 4: Calculate the Ratio of Volumes
Calculate the ratio of the final volume to the initial volume:
VfinalVinitial=250L25L=10
Step 5: Calculate the Logarithm
Now calculate the logarithm:
log(10)=1
Step 6: Substitute Values into the Work Formula
Now substitute all the values into the work formula:
W=−2.303×1mol×8.314J/(mol K)×300K×1
Step 7: Perform the Calculation
Calculate the work done:
W=−2.303×1×8.314×300
W=−5744.19J
Step 8: Final Answer
Thus, the work done when 1 mole of gas expands isothermally from 25 L to 250 L is approximately:
W≈−5744J
- Number of moles (n) = 1 mole
- Initial volume (V_initial) = 25 L
- Final volume (V_final) = 250 L
- Constant pressure (P) = 1 atm
- Temperature (T) = 300 K
For isothermal expansion of an ideal gas, the work done (W) can be calculated using the formula:
W=−2.303nRTlog(VfinalVinitial)
Since the pressure is given in atm and we want the work in joules, we will use the gas constant R=8.314J/(mol K).
Calculate the ratio of the final volume to the initial volume:
VfinalVinitial=250L25L=10
Now calculate the logarithm:
log(10)=1
Now substitute all the values into the work formula:
W=−2.303×1mol×8.314J/(mol K)×300K×1
Calculate the work done:
W=−2.303×1×8.314×300
W=−5744.19J
Thus, the work done when 1 mole of gas expands isothermally from 25 L to 250 L is approximately:
W≈−5744J
Topper's Solved these Questions
- THERMODYNAMICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - HIGHER ORDER THINKING SKILLS
8 Videos
- THERMODYNAMICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - NCERT EXEMPLAR PROBLEMS
11 Videos
- THE S-BLOCK ELEMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THE S-BLOCK ELEMENTSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
The pressure-volume of varies thermodynamic process is shown in graphs:
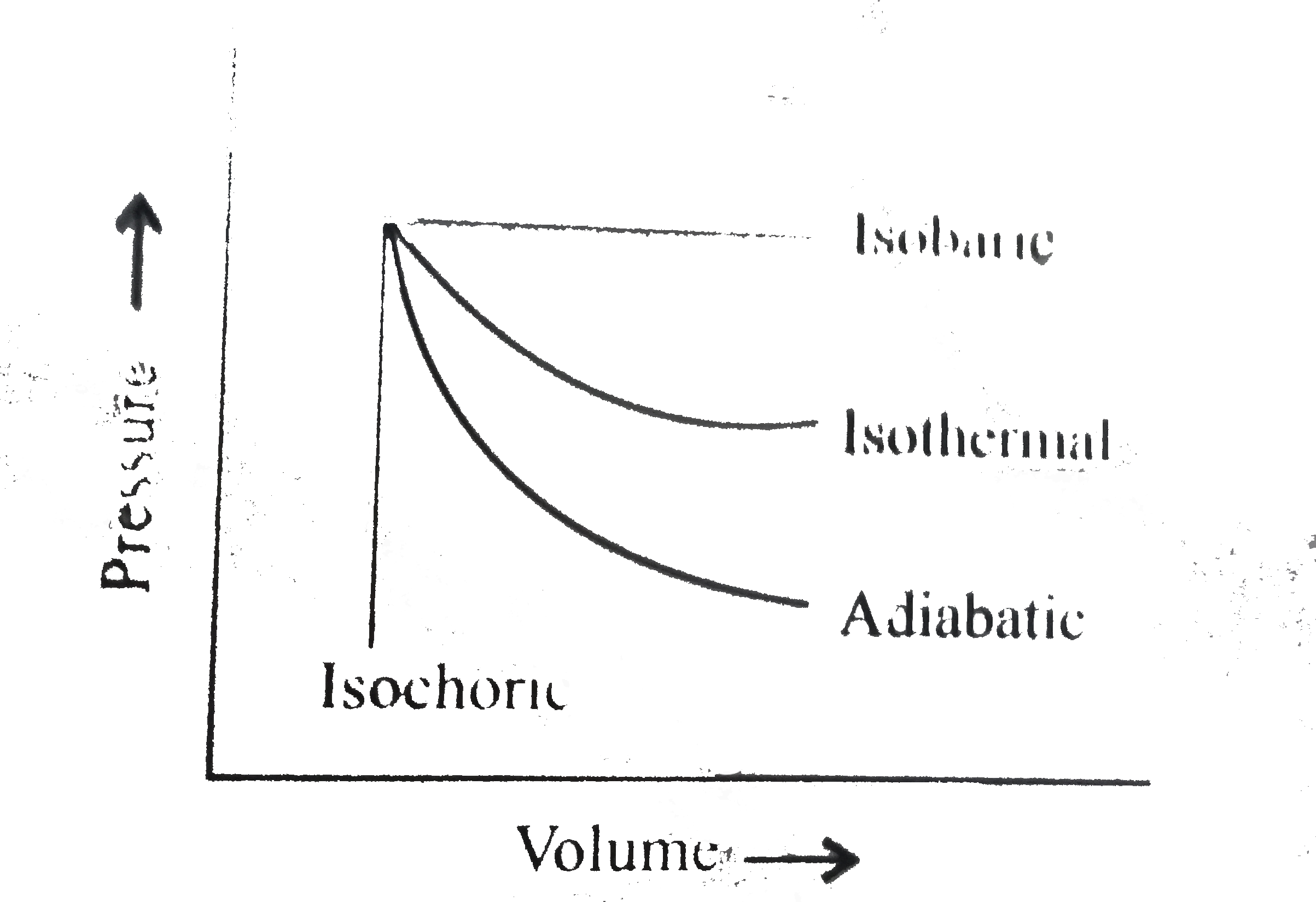
Work is the mole of transference of energy. It has been observed that reversible work done by the system is the maximum obtainable work.
wrev>wirr
The works of isothermal and adiabatic processes are different from each other.
wisothermal reversible=−2.303nRTlog10(V2V1)
=2.303nRTlog10(P2P1)
wadiabatic reversible=CV(T1−T2)
Calculate work done when 1 mole of an ideal gas is expanded reversibly from 30L to 60L at a constant temperature of 300K
View SolutionCalculate the work done when 1 mol of an ideal gas is compressed reversibly from 1 bar to 4 bar at a constant temperature of 300 K
View Solution
Knowledge Check
What will be the work done when one mole of a gas expands isothermally from 15 L to 50 L against a constant pressure of 1 atm at 25∘C?
A−3542calB−843.3calC−718calD−60.23calWhat is the entropy change when 1 mole oxygen gas expands isothermally and reversibly from an initial volume of 10 L to 100 L at 300 K ?
A19.14 J K−1B109.12 J K−1C29.12 J K−1D10 J K−1
Calculate the work done when 1 mole of a gas expands reversibly and isothermally from 5 atm to 1 atm at 300 K. [Value of log 5 = 0.6989].
View SolutionA gas can expand from 100mL to 250mL under a constant pressure of 2 atm. The work done by the gas is
View Solutionone mole of an ideal gas at 300k in thermal contact with surroundings expands isothermally from 1.0 L to 2.0 L against a constant presses of 3.0 atm. In this process. The change in entropy of surrroundings (ΔS) in J−1 is
(1 L atm = 101.3 J)
View SolutionOne mole of an ideal gas expands isothermally from 10 L to 100 L. Change in entropy of the process will be
View SolutionOne mole of an ideal gas is expanded from a volume of 3L to 5L under a constant pressure of 1 atm. Calculate the work done by the gas.
View SolutionWhat should be the value of final temperature so that 1 L gas becomes 2.5 L at constant pressure if initial temperature was 300 K?
View Solution
