5 N of force is required to stretch a spring by 3 cm. If the spring is divided into four equal sections, then calculate the force required to stretch one section by 4 cm.
To solve the problem step by step, we will follow these calculations:
Step 1: Determine the spring constant (K)
Given that a force of 5 N stretches the spring by 3 cm, we can use Hooke's Law, which states:
F=kx
Where:
- F = force applied (5 N)
- k = spring constant
- x = extension of the spring (3 cm = 0.03 m)
Rearranging the formula to find k:
k=Fx
Substituting the values:
k=5N0.03m
Calculating k:
k=50.03=166.67N/m
Step 2: Determine the spring constant for one section
Since the spring is divided into four equal sections, the length of one section is one-fourth of the original length. The spring constant for one section, k′, is given by:
k′=4k
Calculating k′:
k′=4×166.67N/m=666.67N/m
Step 3: Calculate the force required to stretch one section by 4 cm
Now we need to find the force required to stretch one section by 4 cm (0.04 m). Using Hooke's Law again:
F′=k′x′
Where:
- F′ = force required
- k′ = spring constant for one section (666.67 N/m)
- x′ = extension of the section (4 cm = 0.04 m)
Substituting the values:
F′=666.67N/m×0.04m
Calculating F′:
F′=26.67N
Final Answer
The force required to stretch one section of the spring by 4 cm is approximately 26.67 N.
---
Given that a force of 5 N stretches the spring by 3 cm, we can use Hooke's Law, which states:
- F = force applied (5 N)
- k = spring constant
- x = extension of the spring (3 cm = 0.03 m)
Since the spring is divided into four equal sections, the length of one section is one-fourth of the original length. The spring constant for one section, k′, is given by:
Now we need to find the force required to stretch one section by 4 cm (0.04 m). Using Hooke's Law again:
- F′ = force required
- k′ = spring constant for one section (666.67 N/m)
- x′ = extension of the section (4 cm = 0.04 m)
The force required to stretch one section of the spring by 4 cm is approximately 26.67 N.
Topper's Solved these Questions
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Conceptual Questions
Explore 18 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:TOUGH & TRICKY PROBLEMS
Explore 9 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:PRACTICE PROBLEMS
Explore 15 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:CHAPTER PRACTICE TEST
Explore 16 Videos
- PHYSICAL WORLD Book:MODERN PUBLICATIONChapter:PHYSICAL WORLD Exercise:Revision exercises (Long answer questions)
Explore 6 Videos
Similar Questions
A force of 1N is required to stretch a spring by 1.5cm. If the spring is cut into three equal parts, find the force required to stretch one part by 3 cm.
View Solution20 J work is required to stretch a spring through 0.1 m . Find the force constant of the spring. If the spring is further stretched through 0.1 m. Calculate work done.
View Solution
Knowledge Check
When a force of 0.1 N is applied, the spring is stretched by 1.5 cm. The spring is cut into three parts and one part is stretched by 3 cm. Find the force required for doing so.
A0.2 NB0.3 NC0.4 ND0.6 NWhen a force of 0.1 N is applied, the spring is stretched by 1.5 cm. The spring is cut into three parts and one part is stretched by 3 cm. Find the force required for doing so.
A0.2 NB0.3 NC0.4 ND0.6 NA spring of spring constant 5×103N/m is stretched by 4 cm from its unstreched of position. Then the work required to stretch it further by 4 cm is
A6 NB12 NC18 ND3 N
A force of 20.0 N is required to hold a spring stretched by 5.0 cm from its equilibrium position. How much work was done in stretching the spring ?
View SolutionA spring of spring constant 5×103N/m is stretched initially by 5 cm from the unstretched position. The work required to further stretch the spring by another 5 cm is .
View SolutionA spring of constant 5×103N/m is stretched initially by 5 cm from the unstreched position. Then the work required to stretch it further by another 5 cm is:
View SolutionThe force required to stretch a spring varies with the distance as shown in figure. If the experiment is performed with the above spring of half the length, the line OA will
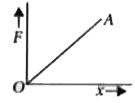
View Solution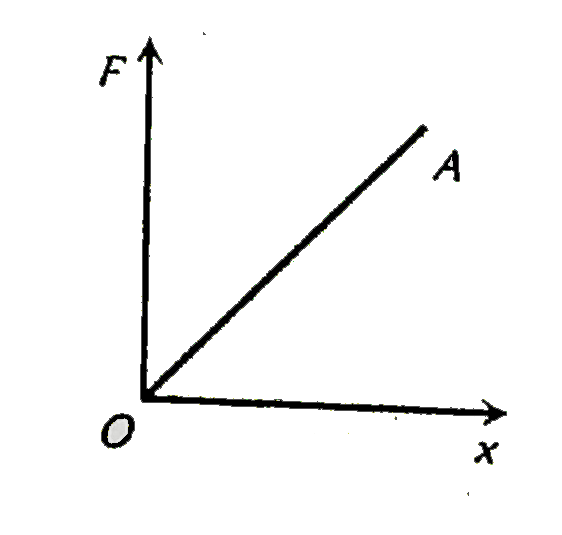
The force required to stretch a spring varies with the distance a shown in the figure. If the experiment is performed with the above spring of half length, the line OA will
View Solution