Calculate the frequency of oscillations of a mass m = 10 kg in the following arangement of springs. (Given k1=k2=k3=k4=k=3 N/m)
0.055 Hz
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Conceptual Questions18videos
OSCILLATIONS
- BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - TOUGH & TRICKY PROBLEMS9videos
OSCILLATIONS
- BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - PRACTICE PROBLEMS15videos
OSCILLATIONS
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST16videos
MOTION IN A STRAIGHT LINE
- BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)6videos
PHYSICAL WORLD
Similar Questions
Two springs of force constants k1 and k2 are joined together and the combination is attached to a mass m resting on a frictionless table at one end and clamped to a fixed support at the other. Show the frequency of oscillation of the mass is f=12π√k1k2(k1+k−(2))m
[Hint: Let the mass be displaced by x and the clamped end of the second spring by x′. Then mf = −k1(x−x′). Considering the first spring and the mass as a single system we have mf =−k2x′]View SolutionIf the angular frequency of small oscillations of a thin uniform vertical rod of mass m and length l hinged at the point O (Fig.) is √nl, then find n. The force constant for each spring is K/2 and take K=2mgl. The springs are of negiligible mass. (g=10m/s2)
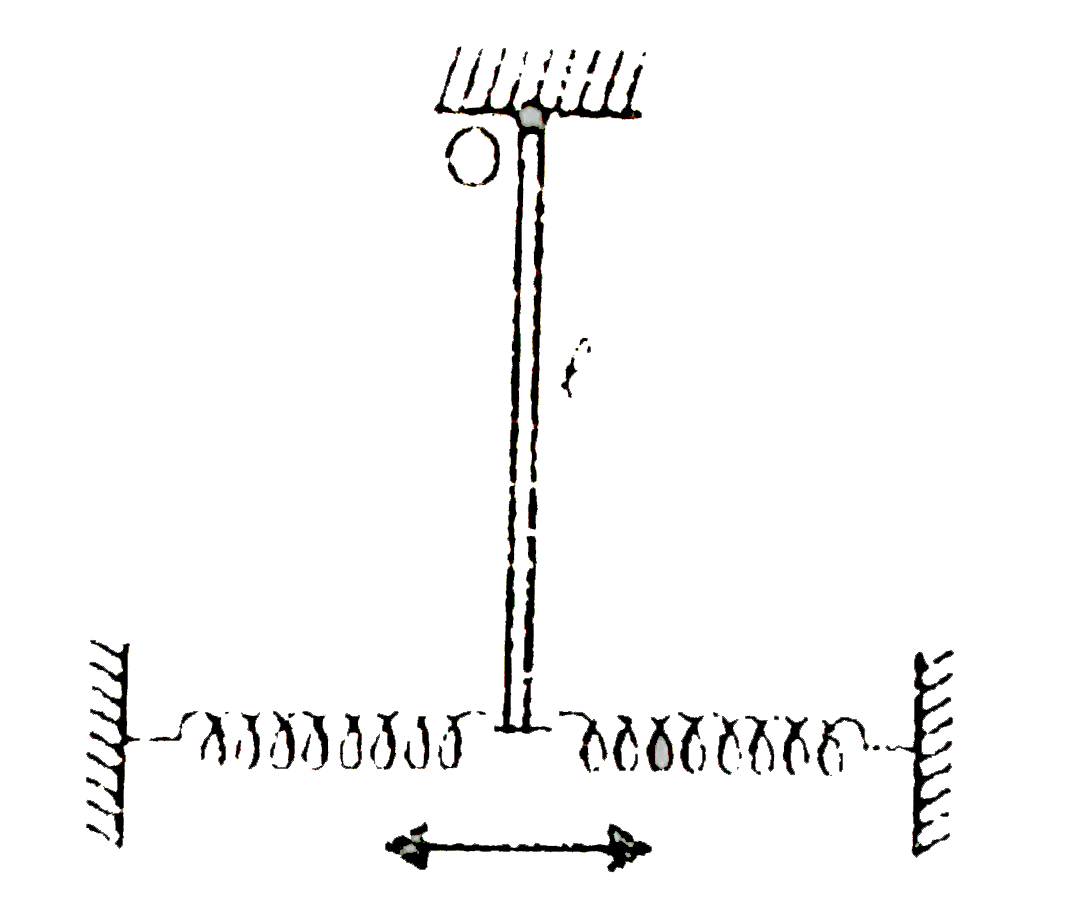View Solution
Knowledge Check
- Question 1 - Select One
Two springs of force constants k1 and k2, are connected to a mass m as shown. The frequency of oscillation of the mass is f. If both k1 and k2 are made four times their original values, the frequency of oscillation becomes
_E01_383_Q01.png)
Af/2Bf/4C4fD2f - Question 2 - Select One
Two springs, of force constants k1 and k2, are connected to a mass maas shown. The frequency of oscillation of mass is f. If both k1 and k2 are made four times their original values, the frequency of oscillation becomes
Af/2Bf/4C4fD2f
If the angular frequency of small oscillations of a thin uniform vertical rod of mass m and length l hinged at the point O (Fig.) is √nl, then find n. The force constant for each spring is K/2 and take K=2mgl. The springs are of negiligible mass. (g=10m/s2)
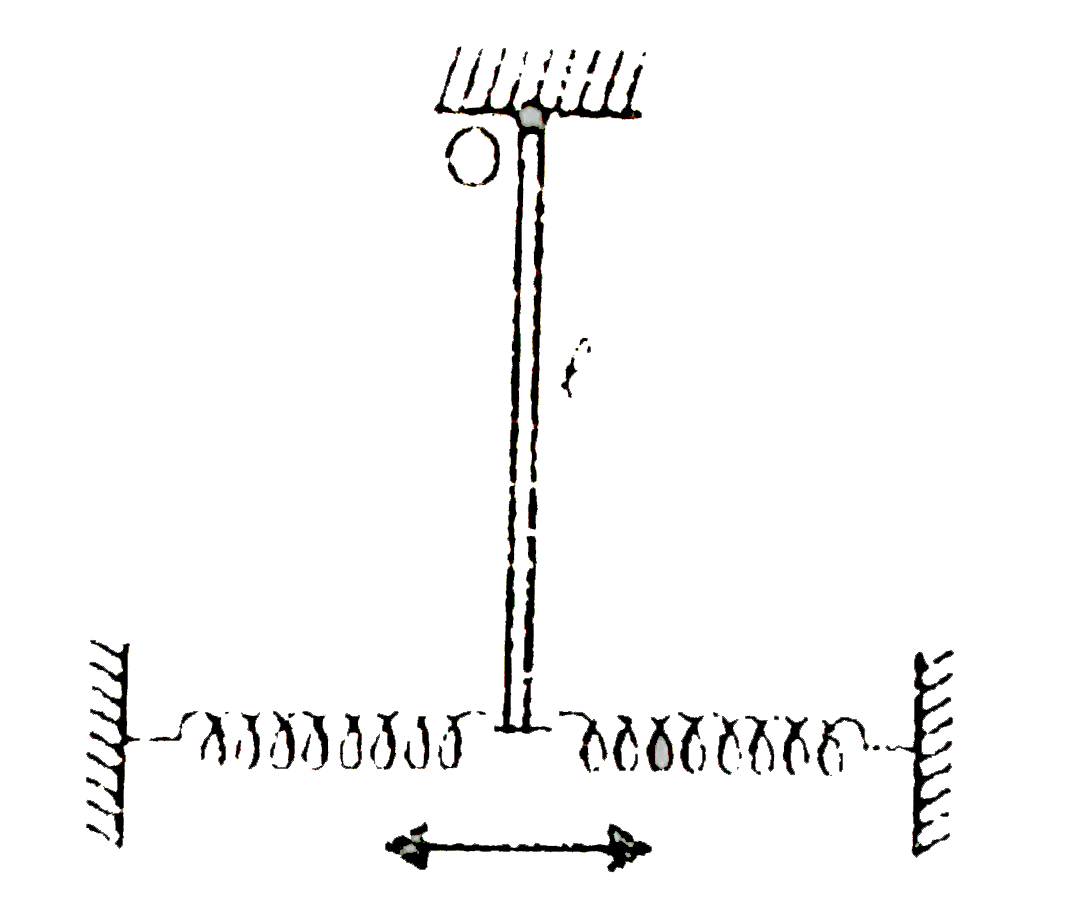View SolutionCalculate the concentration of all species of significant concentrations presents in 0.1MH3PO4 solution. ltbrlt K1=7.5×10−3,K2=6.2×10−8,K#=3.6×10−13
View SolutionThe figure shows a mass M attached to a series arrangement of two springs of spring constants k1andk2 where k2=2k1. If the mass M oscillates in simple harmonic motion with amplitude A, the amplitude of the point O is αAβ. Find β−α.
View SolutionCalculate the concentration of all species of significant concentrations presents in 0.1MH3PO4 solution. lf K1=7.5×10−3,K2=6.2×10−8,K3=3.6×10−13
View SolutionIn the arrangement shown in figure, pulleys are light and spring are ideal. K1, k2, k3and k4 are force constant of the spring. Calculate period of small vertical oscillations of block of mass m.
View SolutionSprings of spring constant k, 2k, 4k , 8k, …. Are connected in series. A block of mass 50 kg is attached to the lower end of the last spring and the system is set into oscillation. If k = 3.0 N/cm, what is the time period of oscillations ?
View Solution