A 0.50 kg meter stick can rotate around an axis perpendicular to the stick. Find the difference in the stick's rotational inertia about the rotation axis if that axis is initially at the point marked "40cm" and then at the point marked "10cm".
To solve the problem of finding the difference in the rotational inertia of a 0.50 kg meter stick about two different axes (one at 40 cm and the other at 10 cm), we can follow these steps:
1. Identify the Mass per Unit Length:
The total mass of the meter stick is 0.50 kg, and its length is 1 meter (100 cm). Therefore, the mass per unit length (λ) can be calculated as:
λ=0.50kg100cm=0.005kg/cm
2. Calculate the Moment of Inertia about the 40 cm Axis (I1):
The moment of inertia (I) of a uniform rod about an axis perpendicular to it and at a distance d from one end is given by:
I=13mL2
where m is the mass of the rod and L is its length.
For the part of the stick from 0 cm to 40 cm:
- Length (L1) = 40 cm = 0.4 m
- Mass (m1) = 0.005kg/cm×40cm=0.20kg
For the part of the stick from 40 cm to 100 cm:
- Length (L2) = 60 cm = 0.6 m
- Mass (m2) = 0.005kg/cm×60cm=0.30kg
Now, calculate I1:
I1=13m1L12+13m2L22
I1=13(0.20kg)(0.4m)2+13(0.30kg)(0.6m)2
I1=13(0.20×0.16)+13(0.30×0.36)
I1=13(0.032)+13(0.108)
I1=0.01067+0.036=0.04667kg m2
3. Calculate the Moment of Inertia about the 10 cm Axis (I2):
Using the same formula for the moment of inertia:
For the part of the stick from 0 cm to 10 cm:
- Length (L1) = 10 cm = 0.1 m
- Mass (m1) = 0.005kg/cm×10cm=0.05kg
For the part of the stick from 10 cm to 100 cm:
- Length (L2) = 90 cm = 0.9 m
- Mass (m2) = 0.005kg/cm×90cm=0.45kg
Now, calculate I2:
I2=13m1L12+13m2L22
I2=13(0.05kg)(0.1m)2+13(0.45kg)(0.9m)2
I2=13(0.05×0.01)+13(0.45×0.81)
I2=13(0.0005)+13(0.3645)
I2=0.0001667+0.1215=0.12167kg m2
4. Calculate the Difference in Rotational Inertia:
ΔI=I2−I1
ΔI=0.12167kg m2−0.04667kg m2
ΔI=0.075kg m2
Final Answer:
The difference in the stick's rotational inertia about the two axes is 0.075kg m2.
The total mass of the meter stick is 0.50 kg, and its length is 1 meter (100 cm). Therefore, the mass per unit length (λ) can be calculated as:
λ=0.50kg100cm=0.005kg/cm
The moment of inertia (I) of a uniform rod about an axis perpendicular to it and at a distance d from one end is given by:
I=13mL2
where m is the mass of the rod and L is its length.
- Length (L1) = 40 cm = 0.4 m
- Mass (m1) = 0.005kg/cm×40cm=0.20kg
- Length (L2) = 60 cm = 0.6 m
- Mass (m2) = 0.005kg/cm×60cm=0.30kg
I1=13m1L12+13m2L22
I1=13(0.20kg)(0.4m)2+13(0.30kg)(0.6m)2
I1=13(0.20×0.16)+13(0.30×0.36)
I1=13(0.032)+13(0.108)
I1=0.01067+0.036=0.04667kg m2
Using the same formula for the moment of inertia:
For the part of the stick from 0 cm to 10 cm:
- Length (L1) = 10 cm = 0.1 m
- Mass (m1) = 0.005kg/cm×10cm=0.05kg
- Length (L2) = 90 cm = 0.9 m
- Mass (m2) = 0.005kg/cm×90cm=0.45kg
I2=13m1L12+13m2L22
I2=13(0.05kg)(0.1m)2+13(0.45kg)(0.9m)2
I2=13(0.05×0.01)+13(0.45×0.81)
I2=13(0.0005)+13(0.3645)
I2=0.0001667+0.1215=0.12167kg m2
ΔI=I2−I1
ΔI=0.12167kg m2−0.04667kg m2
ΔI=0.075kg m2
The difference in the stick's rotational inertia about the two axes is 0.075kg m2.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)43videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)7videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - CHECKPOINT18videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)5videos
RELATIVITY
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)2videos
RIGID BODY DYNAMICS-II
Similar Questions
Figure shows a thin, uniform rod of mass M and length L, on an x axis with the origin at the rod's center.
(a) What is the rotational inertia of the rod about the perpendicular rotation axis through the center?
(b) What is the rod's rotational inertia I about a new rotation axis that is perpendicular to the rod and through the left end?View SolutionA uniform stick of length l is hinged so as to rotated about a harmonic axis perpendicular to the stick, at a distance from the center . Find the value of x, for which the time period is minimum.
View Solution
Knowledge Check
- Question 1 - Select One
The earth rotates around an axis pointing towards -
AThe moonBThe pole starCThe sunDVenus - Question 2 - Select One
A uniform disc of mass 2kg is rotated about an axis perpendicular to the plane of the disc . If radius of gyration is 50cm, then the M.I. of disc about same axis is
A0.25kgm2B0.5kgm2C2kgm2D1kgm2 - Question 3 - Select One
if rod is rotated about an axis passing through its mid-point , the potential difference between the ends of rod is
ABωL24BBωL22C3BωL24Dzero
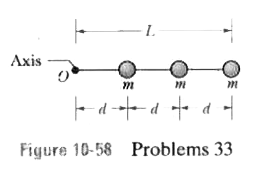
Figure 10-58 shows three 0.0100 kg particles that have been glued to a rod of length L = 8.00 cm and negligible mass. The assembly can rotate around a perpendicular axis through point O at the left end. If we remove one particle (that is, 33% of the mass), by what percentage does the rotational inertia of the assembly around the rotation axis decrease when that removed particle is (a) the inner-most one and (b) the outermost one?
 View Solution
View SolutionCalculate the moment of inertia of each particle in Fig. about the indicated axis of rotation.
 View Solution
View SolutionA metre stick is pivoted about its centre. A piece of wax of mass 20 g travelling horizontally and perpendicular to it at 5 m/s strikes and adheres to one end of the stick so that the stick starts to rotate in a horizontal circle. Given the moment of inertia of the stick and wax about the pivot is 0.02 kg m2, the initial angular velocity of the stick is :
View SolutionThe moment of inertia of a metre stick of mass 300 gm , abut an axis at right angles to the stick and located at 30 cm mark , is
View SolutionA uniform stick of length l is mounted so as to rotate about a horizontal axis perpendicular to the stick and at a distance d from the centre of mass. The time period of small oscillation has a minimum value when d/l is
View Solution

