A cord with negligible mass is wrapped around a pulley that is a uniform disk of mass 5.00 kg and radius 0.300 m and that can rotate without friction about its central axis. A 1.0 kg bucket is attached at the free end of the cord hanging down from the pulley and then released at time t = 0. The cord begins to unwrap from the pulley as the bucket descends. At t = 5.00 s, through how many rotations has the pulley turned (the bucket is still descending)?
To solve the problem step by step, we will analyze the forces acting on the bucket and the resulting motion of the pulley.
Step 1: Identify the forces acting on the bucket
The forces acting on the bucket (mass m=1kg) are:
- The gravitational force Fg=mg acting downward.
- The tension T in the cord acting upward.
Using g=9.8m/s2, we can calculate the weight of the bucket:
Fg=mg=1×9.8=9.8N
Step 2: Apply Newton's second law to the bucket
According to Newton's second law, the net force acting on the bucket is equal to the mass of the bucket times its acceleration a:
mg−T=ma
Substituting mg into the equation:
9.8−T=1a(1)
Step 3: Analyze the pulley
The pulley is a uniform disk with mass M=5kg and radius R=0.3m. The moment of inertia I of a disk about its central axis is given by:
I=12MR2
Substituting the values:
I=12×5×(0.3)2=12×5×0.09=0.225kg m2
Step 4: Relate tension and angular acceleration
The torque τ on the pulley due to the tension T is given by:
τ=T⋅R
The angular acceleration α of the pulley is related to the linear acceleration a of the bucket by:
α=aR
Using the equation for torque:
T⋅R=I⋅α
Substituting α:
T⋅R=I⋅aR
Rearranging gives:
T=I⋅aR2
Substituting I:
T=0.225⋅a(0.3)2=0.225⋅a0.09=2.5a(2)
Step 5: Substitute equation (2) into equation (1)
Substituting T from equation (2) into equation (1):
9.8−2.5a=a
Combining like terms:
9.8=3.5a
Solving for a:
a=9.83.5≈2.8m/s2
Step 6: Calculate angular acceleration
Using the relationship between linear acceleration and angular acceleration:
α=aR=2.80.3≈9.33rad/s2
Step 7: Calculate angular displacement after 5 seconds
Using the equation for angular displacement with initial angular velocity ωi=0:
θ=ωit+12αt2
Substituting ωi=0, α≈9.33rad/s2, and t=5s:
θ=0+12⋅9.33⋅(5)2=12⋅9.33⋅25≈116.625rad
Step 8: Convert angular displacement to rotations
To find the number of rotations, we convert radians to rotations:
Number of rotations=θ2π=116.6252π≈116.6256.283≈18.57
Thus, the pulley has completed approximately 19 rotations after 5 seconds.
Final Answer
The pulley has turned approximately 19 rotations after 5 seconds.
The forces acting on the bucket (mass m=1kg) are:
- The gravitational force Fg=mg acting downward.
- The tension T in the cord acting upward.
Fg=mg=1×9.8=9.8N
According to Newton's second law, the net force acting on the bucket is equal to the mass of the bucket times its acceleration a:
mg−T=ma
Substituting mg into the equation:
9.8−T=1a(1)
The pulley is a uniform disk with mass M=5kg and radius R=0.3m. The moment of inertia I of a disk about its central axis is given by:
I=12MR2
Substituting the values:
I=12×5×(0.3)2=12×5×0.09=0.225kg m2
The torque τ on the pulley due to the tension T is given by:
τ=T⋅R
The angular acceleration α of the pulley is related to the linear acceleration a of the bucket by:
α=aR
Using the equation for torque:
T⋅R=I⋅α
Substituting α:
T⋅R=I⋅aR
Rearranging gives:
T=I⋅aR2
Substituting I:
T=0.225⋅a(0.3)2=0.225⋅a0.09=2.5a(2)
Substituting T from equation (2) into equation (1):
9.8−2.5a=a
Combining like terms:
9.8=3.5a
Solving for a:
a=9.83.5≈2.8m/s2
Using the relationship between linear acceleration and angular acceleration:
α=aR=2.80.3≈9.33rad/s2
Using the equation for angular displacement with initial angular velocity ωi=0:
θ=ωit+12αt2
Substituting ωi=0, α≈9.33rad/s2, and t=5s:
θ=0+12⋅9.33⋅(5)2=12⋅9.33⋅25≈116.625rad
To find the number of rotations, we convert radians to rotations:
Number of rotations=θ2π=116.6252π≈116.6256.283≈18.57
Thus, the pulley has completed approximately 19 rotations after 5 seconds.
The pulley has turned approximately 19 rotations after 5 seconds.
Topper's Solved these Questions
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
43 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
7 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - CHECKPOINT
18 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
2 Videos
Similar Questions
A hoop of radius r mass m rotating with an angular velocity ω0 is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it cases to slip ?
View SolutionA rigid body is in pure rotation, that is, undergoing fixed axis rotation. Then which of the following statement(s) are true?
View SolutionA disk can rotate about its central axis like a merry-go-round. Which of the following pairs of values for its initial and final angular positions, respectively, give a negative angular displacement: (a) -3 rad, +5 rad, (b) -3 rad, -7 rad, ( c) 7 rad, -3 rad?
View SolutionA bomb is designed to explode 2.00 s after it is armed. The bomb is launched from Earth and accelerated to an unknown final speed. After reaching its final speed, however, the bomb is observed by people on Earth to explode 4.25 s after it is armed. What is the final speed of the bomb just before it explodes (in terms of c)?
View SolutionA uniform circular disc of mass 50kg and radius 0.4 m is rotating with an angular velocity of 10rads−1 about its own axis, which is vertical. Two uniform circular rings, each of mass 6.25 kg and radius 0.2 m, are gently placed symmetrically on the disc in such a manner that they are touching each other along the axis of the disc and are horizontal. Assume that the friction is large enough such that the rings are at rest relative to the disc and the system rotates about the original axis. The new angular velocity (∈reds−1) of the system is
View SolutionA mass m is attached to a pulley through a cord as shown in figure. The pulley is a solid disk with radius R. The cord does not slip on the disk. The mass is released from rest at a height h from the ground and at the instant the mass reaches the ground, the disk is rotating with angular velocity ω. Find the mass of the disk.
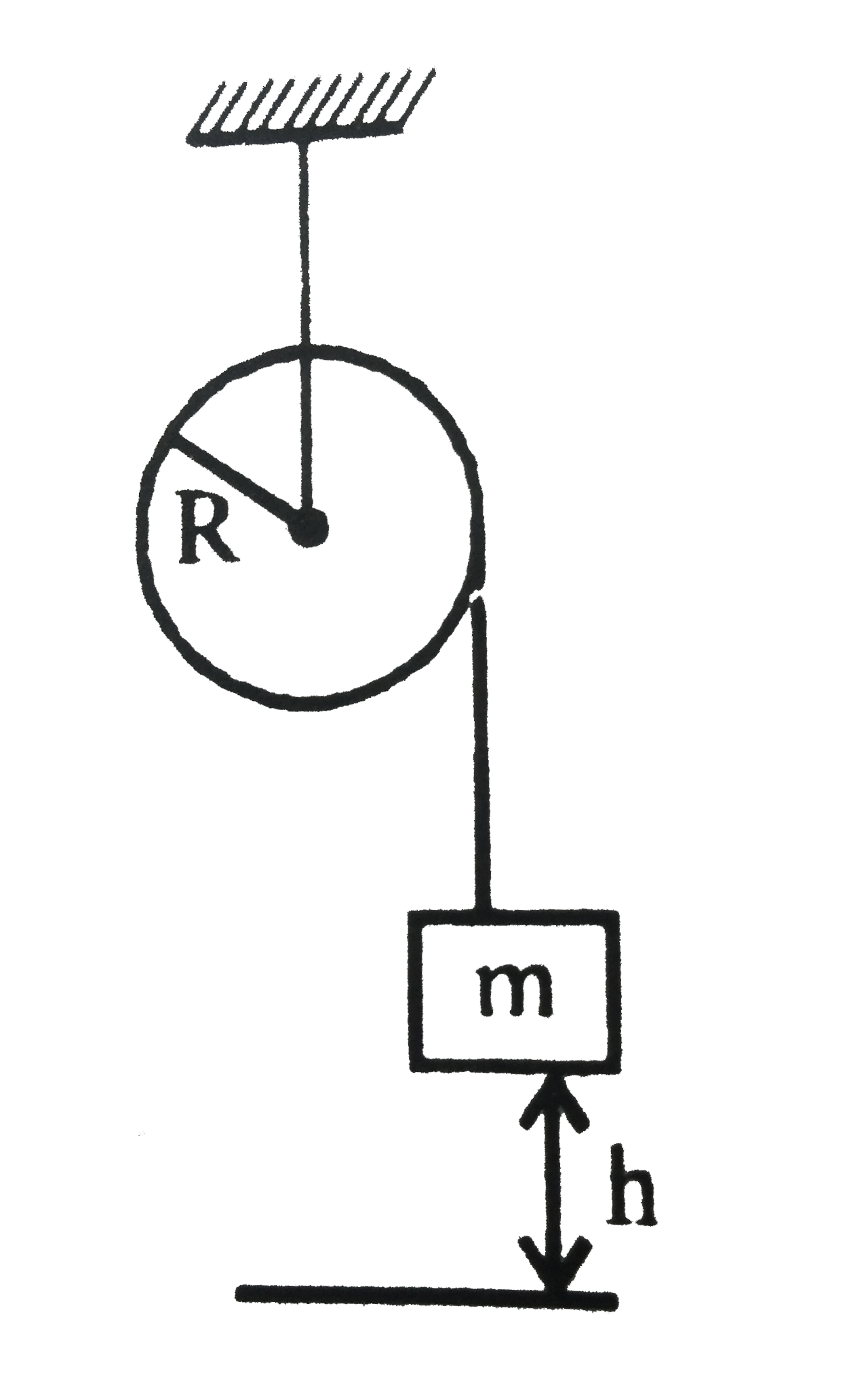 .
.
View SolutionA pulley has the shape of a uniform solid disc of mass 2kg and radius 0.5m. A string is wrapped over its rim and is pulled by a force of 2.5N. The pulley is free to rotate about its axis. Initially, the pulley is at rest. Find the angular velocity and angle rotated by pulley in 10s.

View SolutionA small bucket of mass M kg is attached to a lone inextensible cord of length L m. The bucket is released from rest when the cord is in a horizontal position. At its lowest position, the bucket scoops up m kg of water and swings up to a height h. The height h in meter is :-
View SolutionA fixed pulley of radius 20 cm and moment of inertia 0.32 kg. m^(2) about its axle has a massless cord wrapped around its rim. A mass M of 2 kg is attached to the end of the cord. The pulley can rotate about its axis without any friction. The acceleration of the mass M is :- (Assuming g=10m//s^(2) )
View Solutionएक घर्षण रहित घिरनी पर लिपटी डोरी से m द्रव्यमान लटका है। घिरनी का द्रव्यमान m तथा त्रिज्या R हैं। यदि एक समान वृत्तीय डिस्क है तो घिरनी पर डोरी के नसलने पर द्रव्यमान m का त्वरण होगा : -
View SolutionA cord is wrapped on a pulley (disk) of mass M and radius R as shown in figure. To one end of the cord, a block of mass M is connected as shown and to other end in (a) a force of 2 Mg and in (b) a block of mass 2 M. Let angular acceleration of the disk in (a) and (b) is alpha_(A) and alpha_(B) respectively, then (cord is not slipping on the pulley)
View SolutionA, B और C तीन वस्तुएँ जिनके द्रव्यमान क्रमशः 4 किग्रा, 1 किग्रा और 3 किग्रा हैं , चित्रानुसार डोरियों द्वारा एक घर्षणरहित घिरनी से लटकायी गयी है । उभयनिष्ठ त्वरण और दोनों डोरियों में तनाव की गणना कीजिए ।
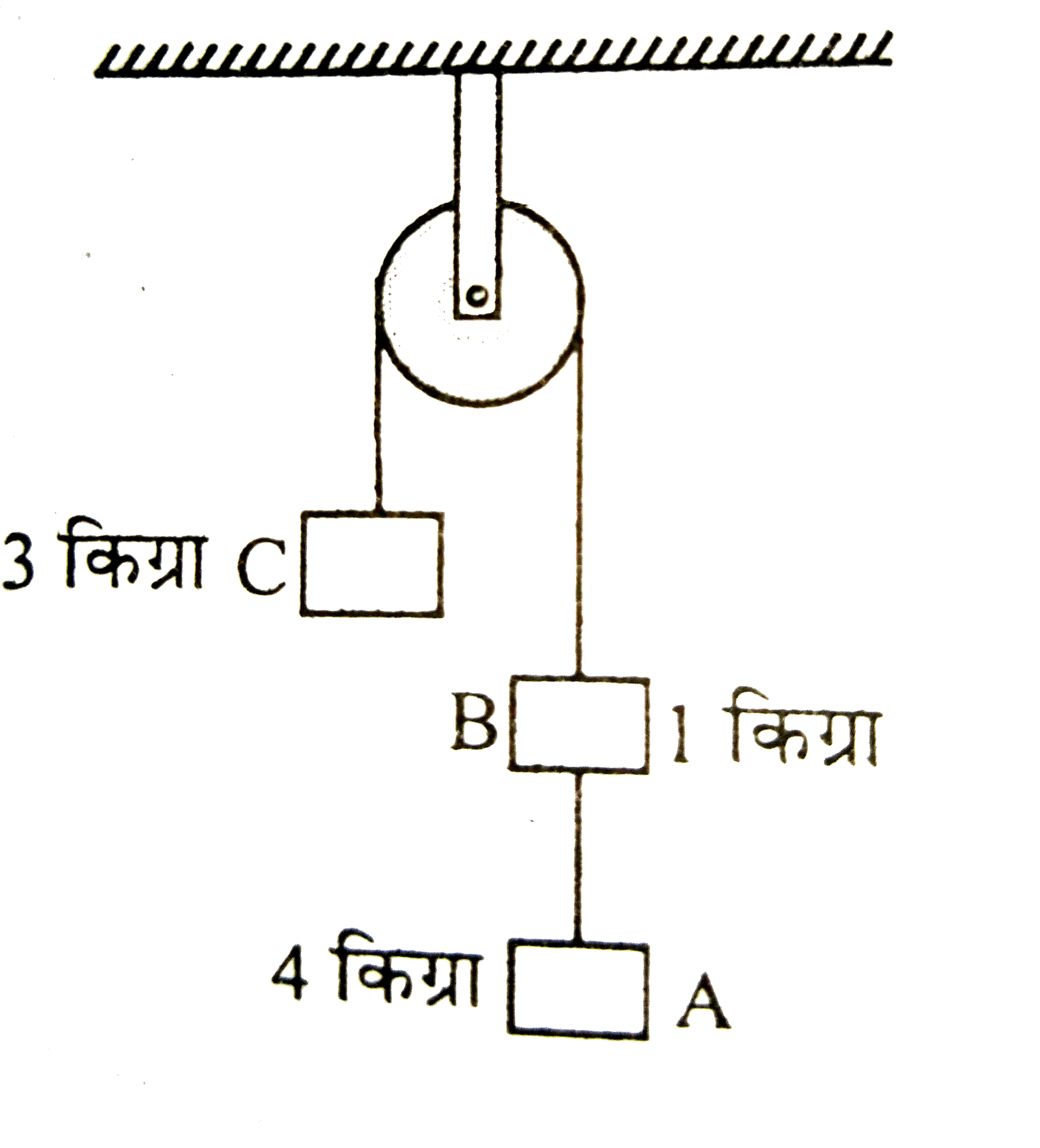
View SolutionA string of negligible mass is wrapped on a cylindrical pulley of mass M and radius R. The other end of string is tied to a bucket of mass m. If the pulley rotates about a horizontal axis then the tension in the string is :
View SolutionAn empty bucket of mass 1 kg attached by a light cord passed over a pulley of a water well is released from rest. If the pulley assembly is assumed to be a uniform solid cylinder of mass 8 kg and free to rotate about its axis without any friction, then the speed of the bucket as it hits the water 16 m below is (take, g = 10ms−2)
View SolutionFigure 5-20 shows a block S (the sliding block) with mass M = 3.3 kg. The block is free to move along a horizontal frictionless surface and connected, by a cord that wraps over a frictionless pulley, to a second block H (the hanging block), with mass m = 2.1 kg. The cord and pulley have negligible masses compared to the blocks (they are "massless"). The hanging block H falls as the sliding block S accelerates to the right. Find (a) the acceleration of block S, (b) the acceleration of block H, and ( c ) the tension in the cord.
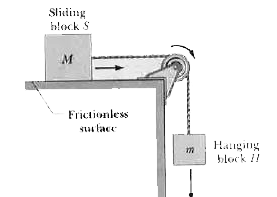
Figure 5.20 A block S of mass M is connected to a block H of mass m by a cord that wraps over a pulley.
View Solution
