A 1 kg ball moving with a speed of 20 m/s strikes a hard wall at an angle of 30∘ with the wall. It is reflected with the same speed at the same angle. If the ball is in contact with the wall for 0.5 seconds, the average force acting on the wall is
96 N
48 N
24 N
40 N
The correct Answer is:D
To solve the problem, we need to calculate the average force acting on the wall when a ball strikes it and is reflected back. Here’s a step-by-step solution:
Step 1: Understand the Initial Conditions
- Mass of the ball (m) = 1 kg
- Initial speed of the ball (v) = 20 m/s
- Angle of incidence with the wall (θ) = 30 degrees
- Time of contact with the wall (Δt) = 0.5 seconds
Step 2: Resolve the Initial Velocity into Components
The velocity of the ball can be resolved into two components:
- Horizontal Component (v_x):
vx=v⋅cos(θ)=20⋅cos(30∘)=20⋅√32=10√3m/s
- Vertical Component (v_y):
vy=v⋅sin(θ)=20⋅sin(30∘)=20⋅12=10m/s
Step 3: Calculate Initial Momentum
The initial momentum vector (P_initial) can be expressed as:
Pinitial=m⋅v=(1kg)⋅(10√3^i−10^j)kg m/s
Pinitial=10√3^i−10^jkg m/s
Step 4: Calculate Final Momentum
After striking the wall, the horizontal component of the velocity reverses direction while the vertical component remains unchanged:
- Final Horizontal Component (v'_x):
v′x=−20⋅cos(30∘)=−10√3m/s
- Final Vertical Component (v'_y):
v′y=20⋅sin(30∘)=10m/s
Thus, the final momentum vector (P_final) is:
Pfinal=m⋅v′=(1kg)⋅(−10√3^i+10^j)kg m/s
Pfinal=−10√3^i+10^jkg m/s
Step 5: Calculate Change in Momentum (ΔP)
The change in momentum (ΔP) is given by:
ΔP=Pfinal−Pinitial
Substituting the values:
ΔP=(−10√3^i+10^j)−(10√3^i−10^j)
ΔP=−20√3^i+20^jkg m/s
Step 6: Calculate the Magnitude of Change in Momentum
The magnitude of ΔP can be calculated as:
|ΔP|=√(−20√3)2+(20)2=√1200+400=√1600=40kg m/s
Step 7: Calculate Average Force (F_avg)
The average force acting on the wall can be calculated using the formula:
Favg=ΔPΔt
Substituting the values:
Favg=40kg m/s0.5s=80N
Final Answer
The average force acting on the wall is 80 N.
---
- Mass of the ball (m) = 1 kg
- Initial speed of the ball (v) = 20 m/s
- Angle of incidence with the wall (θ) = 30 degrees
- Time of contact with the wall (Δt) = 0.5 seconds
The velocity of the ball can be resolved into two components:
- Horizontal Component (v_x):
vx=v⋅cos(θ)=20⋅cos(30∘)=20⋅√32=10√3m/s
- Vertical Component (v_y):
vy=v⋅sin(θ)=20⋅sin(30∘)=20⋅12=10m/s
The initial momentum vector (P_initial) can be expressed as:
Pinitial=m⋅v=(1kg)⋅(10√3^i−10^j)kg m/s
Pinitial=10√3^i−10^jkg m/s
After striking the wall, the horizontal component of the velocity reverses direction while the vertical component remains unchanged:
- Final Horizontal Component (v'_x):
v′x=−20⋅cos(30∘)=−10√3m/s
- Final Vertical Component (v'_y):
v′y=20⋅sin(30∘)=10m/s
Pfinal=m⋅v′=(1kg)⋅(−10√3^i+10^j)kg m/s
Pfinal=−10√3^i+10^jkg m/s
The change in momentum (ΔP) is given by:
ΔP=Pfinal−Pinitial
Substituting the values:
ΔP=(−10√3^i+10^j)−(10√3^i−10^j)
ΔP=−20√3^i+20^jkg m/s
The magnitude of ΔP can be calculated as:
|ΔP|=√(−20√3)2+(20)2=√1200+400=√1600=40kg m/s
The average force acting on the wall can be calculated using the formula:
Favg=ΔPΔt
Substituting the values:
Favg=40kg m/s0.5s=80N
The average force acting on the wall is 80 N.
Topper's Solved these Questions
- FORCE BOOK - TARGET PUBLICATIONCHAPTER - FORCE EXERCISE - Competitive Theinking (Miscellaneous)
26 Videos
- ELECTRONS AND PHOTONSBOOK - TARGET PUBLICATIONCHAPTER - ELECTRONS AND PHOTONSEXERCISE - Evaluation Test
19 Videos
- FRICTION IS SOLIDS AND LIQUIDS BOOK - TARGET PUBLICATIONCHAPTER - FRICTION IS SOLIDS AND LIQUIDS EXERCISE - MCQ (EVALUATION TEST)
21 Videos
Similar Questions
A 0.5 kg ball moving with a speed of 12 m/s strikes a hard wall at an angle of 30∘ with the wall. It is reflected with the same speed and at the same angle. If the ball is in contact with the wall for 0.25 s, the average force acting on the wall is :
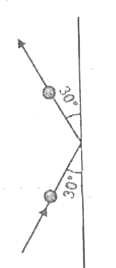
View SolutionA 3.00kg steel hall strikes the wall with a speed of 10.0m/s at an angle of 60∘ with the surface. It bounces off with the same speed and angle. If the ball is in contact with the wall for 0.200s, what is the average force exerted by the wall on the ball?
View Solution
Knowledge Check
A 0.5kg ball moving with a speed of 12m/s strikes a hard wall at an angle of 30∘ with the wall. It is reflected with the same speed and at the same angle . If the ball is in contact with the wall for 0.25s, the average force acting on the wall is
 A48NB24NC12ND96N
A48NB24NC12ND96NA 3 kg ball strikes a heavy rigid wall with a speed of 10ms−1 at an angle of 60∘ with the wall. It gets reflected with the same speed at 60∘ with the wall. If the ball is in contact with the wall for 0.2s, the average force exerted on the ball by the wall is
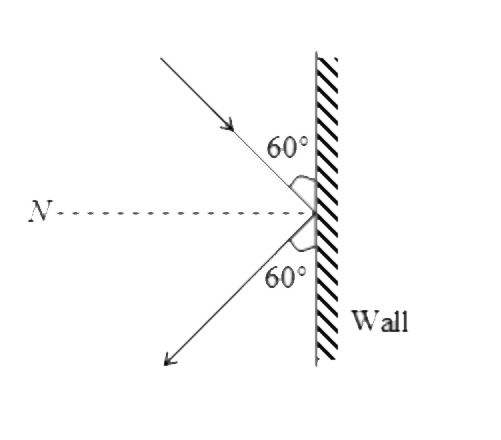 A300NBzeroC150√3ND150 N
A300NBzeroC150√3ND150 NA 1 kg particle strikes a wall with velocity 1 m/s at an angle of 60∘ with the wall and reflects at the same angle. If it remains in contact with wall for 0.1 s, then the force is
A0B10√3 NC30√3ND40√3N
A 3-kg steel ball strikes a wall with a speed of 10.0ms−1 at an angle of 60.0∘ with the surfaces of the wall. The ball bounces off with the same speed and same angle. If the ball was in contact with the wall for 0.2s, find the average force exerted by the wall on the ball.
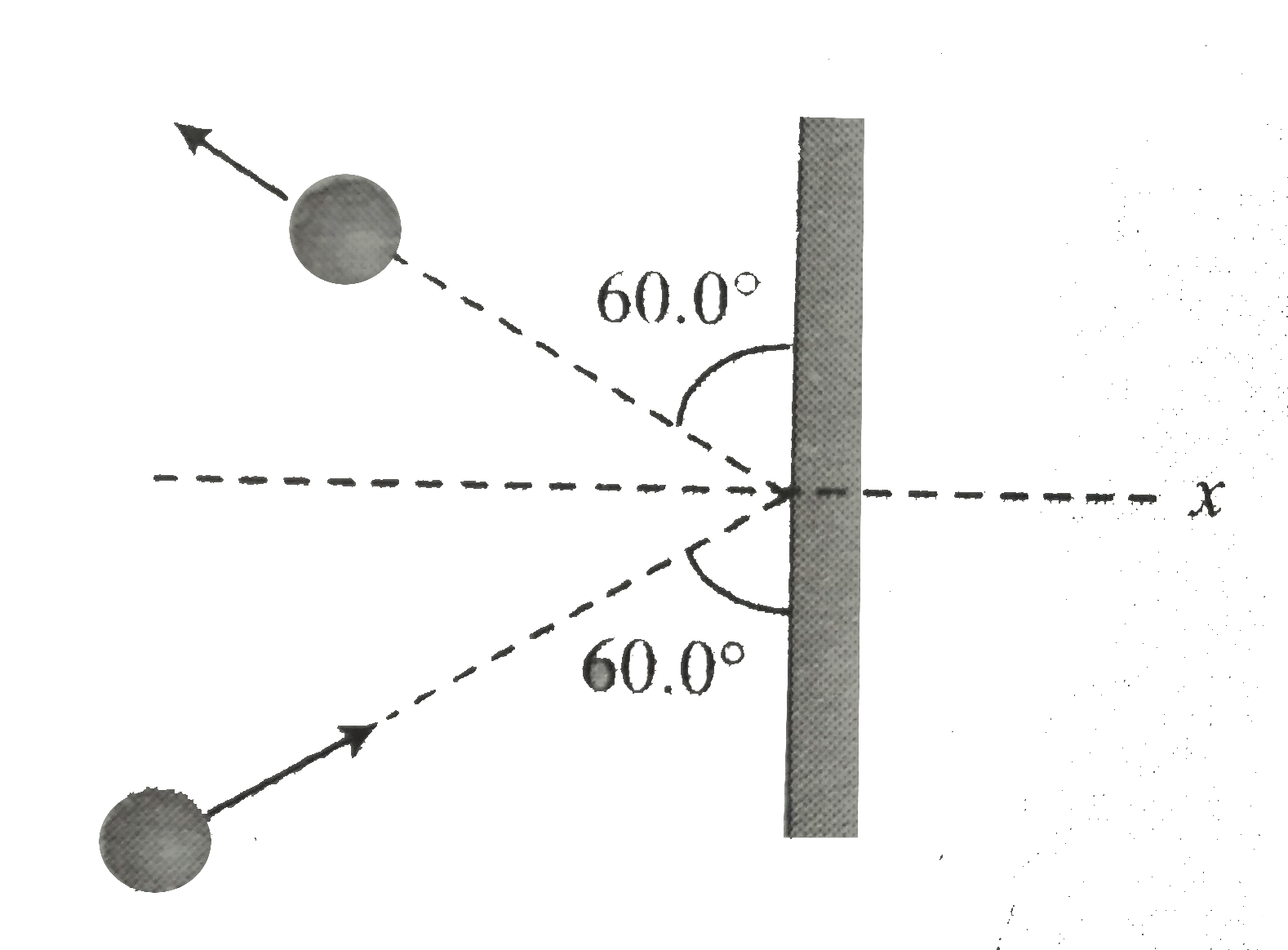
View SolutionA 1 kg particle strikes a wall with velocity 1 m/s at an angle of 60o with the wall and reflects at the same angle. If it remains in contact with the wall for 0.1 s, then the force is
View SolutionA 1kg particle strikes a wall with a velocity 1ms at an angle of 60°with the wall and reflects at the same angle.If it remains in contact with the wall for 0.1sec, then the force is
View SolutionA ball moving with a momentum of 5kgms−1 strikes against a wall at an angle of 45∘ and is reflected at the same angle Calculate the impulse .
View SolutionA ball moving with a momen - tum of 15kgms−1 strickes against the wall at an angle of 30∘ and is reflected back with the same momentum at the same angle . Calculte impulse.
View Solution
