A ball moving with a momentum of 5kgms−1 strikes against a wall at an angle of 45∘ and is reflected at the same angle Calculate the impulse .
The correct Answer is:−7.07kgms−1 .
To solve the problem of calculating the impulse experienced by a ball moving with a momentum of 5kg m/s when it strikes a wall at an angle of 45∘ and is reflected at the same angle, we can follow these steps:
1. Understand the Concept of Impulse:
Impulse is defined as the change in momentum of an object when a force is applied over a period of time. Mathematically, it can be expressed as:
I=Δp
where I is the impulse and Δp is the change in momentum.
2. Identify the Initial Momentum:
The initial momentum of the ball is given as:
p=5kg m/s
3. Resolve Momentum into Components:
Since the ball strikes the wall at an angle of 45∘, we need to resolve the momentum into two components: one parallel to the wall (x-direction) and one perpendicular to the wall (y-direction).
- The component of momentum parallel to the wall (x-direction) is:
px=psin(45∘)=5sin(45∘)=5⋅1√2=5√22kg m/s
- The component of momentum perpendicular to the wall (y-direction) is:
py=pcos(45∘)=5cos(45∘)=5⋅1√2=5√22kg m/s
4. Determine the Change in Momentum:
- After the collision, the component of momentum parallel to the wall remains unchanged, while the perpendicular component reverses direction.
- Therefore, the change in momentum in the y-direction (perpendicular to the wall) is:
Δpy=p′y−py=−5√22−5√22=−5√2kg m/s
- The change in momentum in the x-direction is zero since the momentum component parallel to the wall does not change:
Δpx=0
5. Calculate the Total Change in Momentum:
- The total change in momentum (which contributes to the impulse) is only from the y-direction:
Δp=Δpx+Δpy=0−5√2=−5√2kg m/s
6. Calculate the Impulse:
- The impulse experienced by the ball is equal to the change in momentum:
I=Δp=−5√2kg m/s
- The magnitude of the impulse is:
|I|=5√2kg m/s≈7.07kg m/s
Final Answer:
The impulse experienced by the ball is approximately 7.07kg m/s in the direction opposite to the initial y-component of momentum.
Impulse is defined as the change in momentum of an object when a force is applied over a period of time. Mathematically, it can be expressed as:
I=Δp
where I is the impulse and Δp is the change in momentum.
The initial momentum of the ball is given as:
p=5kg m/s
Since the ball strikes the wall at an angle of 45∘, we need to resolve the momentum into two components: one parallel to the wall (x-direction) and one perpendicular to the wall (y-direction).
- The component of momentum parallel to the wall (x-direction) is:
px=psin(45∘)=5sin(45∘)=5⋅1√2=5√22kg m/s
- The component of momentum perpendicular to the wall (y-direction) is:
py=pcos(45∘)=5cos(45∘)=5⋅1√2=5√22kg m/s
- After the collision, the component of momentum parallel to the wall remains unchanged, while the perpendicular component reverses direction.
- Therefore, the change in momentum in the y-direction (perpendicular to the wall) is:
Δpy=p′y−py=−5√22−5√22=−5√2kg m/s
- The change in momentum in the x-direction is zero since the momentum component parallel to the wall does not change:
Δpx=0
- The total change in momentum (which contributes to the impulse) is only from the y-direction:
Δp=Δpx+Δpy=0−5√2=−5√2kg m/s
- The impulse experienced by the ball is equal to the change in momentum:
I=Δp=−5√2kg m/s
- The magnitude of the impulse is:
|I|=5√2kg m/s≈7.07kg m/s
The impulse experienced by the ball is approximately 7.07kg m/s in the direction opposite to the initial y-component of momentum.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - JEE (Main and Advanced)/ Medical Entrance Special93videos
LAWS OF MOTION
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Integer Type Questions7videos
LAWS OF MOTION
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Fill in the blanks20videos
LAWS OF MOTION
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension4videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks5videos
MATHEMATICAL TOOLS
Similar Questions
A ball moving with a momentum of 5kgms−1 strikes against a wall at an angle of 45∘ and is reflected at the same angle. Calculate the change in momentum.
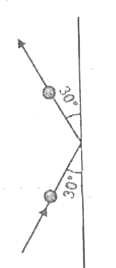
View SolutionA ball moving with a momen - tum of 15kgms−1 strickes against the wall at an angle of 30∘ and is reflected back with the same momentum at the same angle . Calculte impulse.
View Solution
Knowledge Check
- Question 1 - Select One
A 1 kg ball moving with a speed of 20 m/s strikes a hard wall at an angle of 30∘ with the wall. It is reflected with the same speed at the same angle. If the ball is in contact with the wall for 0.5 seconds, the average force acting on the wall is
A96 NB48 NC24 ND40 N - Question 2 - Select One
A 0.5kg ball moving with a speed of 12m/s strikes a hard wall at an angle of 30∘ with the wall. It is reflected with the same speed and at the same angle . If the ball is in contact with the wall for 0.25s, the average force acting on the wall is
 A48NB24NC12ND96N
A48NB24NC12ND96N - Question 3 - Select One
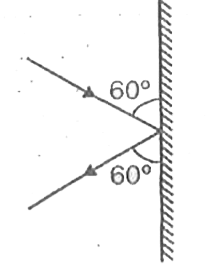
A body of mass 3kg moving with speed 5ms−1 , hits a wall at an angle of 60∘ and return at the same angle. The impact time was 0.2 sec. calculate the force exerted on the wall :
A150√3NB50√3NC100ND75√3N
A 0.5 kg ball moving with a speed of 12 m/s strikes a hard wall at an angle of 30∘ with the wall. It is reflected with the same speed and at the same angle. If the ball is in contact with the wall for 0.25 s, the average force acting on the wall is :
 View Solution
View SolutionThe average force imparted on the wall when a 0.75 kg ball moving with a speed of 18 m/s strikes it at an angle of 60' for a contact time of 0.15 s and gets reflected with the same speed and at the same angle is P newtons. Then, the value of P/10 is: (Take √3=1.73 )
View SolutionA body of mass 3 kg moving with velocity 10 m/s hits a wall at an angle of 60∘ and returns at the same angle. The impact time was 0.2 s. Calculate the force exerted on the wall.
 View Solution
View SolutionA ball of mass 50 g moving at a speed of 2.0 m/s strikes a placne surface at an angle of incidence 450. The ball is reflected by the plane at equal angle of reflection with the same speed. Calculate a. the magnitude of the change in momentum of the ball b. the change in the magnitude of the mometum of the ball.
View SolutionA ball moving with a momemtum 5 kg ms−1 strikes a wall. If the initial and final momenta make equal angles of 45∘, then magnitude in change in momentum is
View Solution

