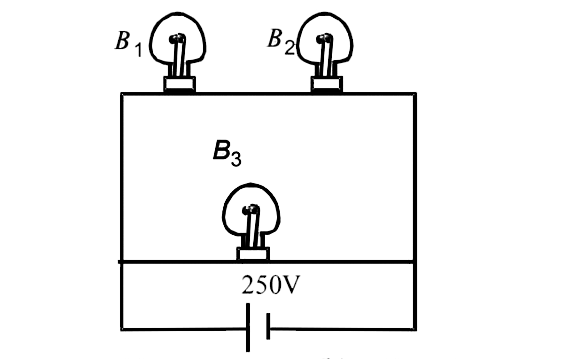
A 100 W bulb B1, and two 60 W bulb B2 and B3, are connected to a 250 V source, as shown in figure. Now W1,W2andW3 are the output powers of the bulbs B1,B2andB3, respectively. Then
A
W1>W2=W3
B
W1>W2>W3
C
W1<W2=W3
D
W1<W2<W3
Video Solution
Text Solution
P=V2R so, R=V2P
∴R1=V2100 and R2=R3=V260
Now, W1=(250)2(R1+R2)2R1
W2=(250)2(R1+R2).R2 and W2=(250)2R3
W1:W2:W3=15:25:64orW1>W2>W3
∴ The correct option is d.
|
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Example Type 6
1 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Miscellaneous Examples
9 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Example Type 4
1 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
Knowledge Check
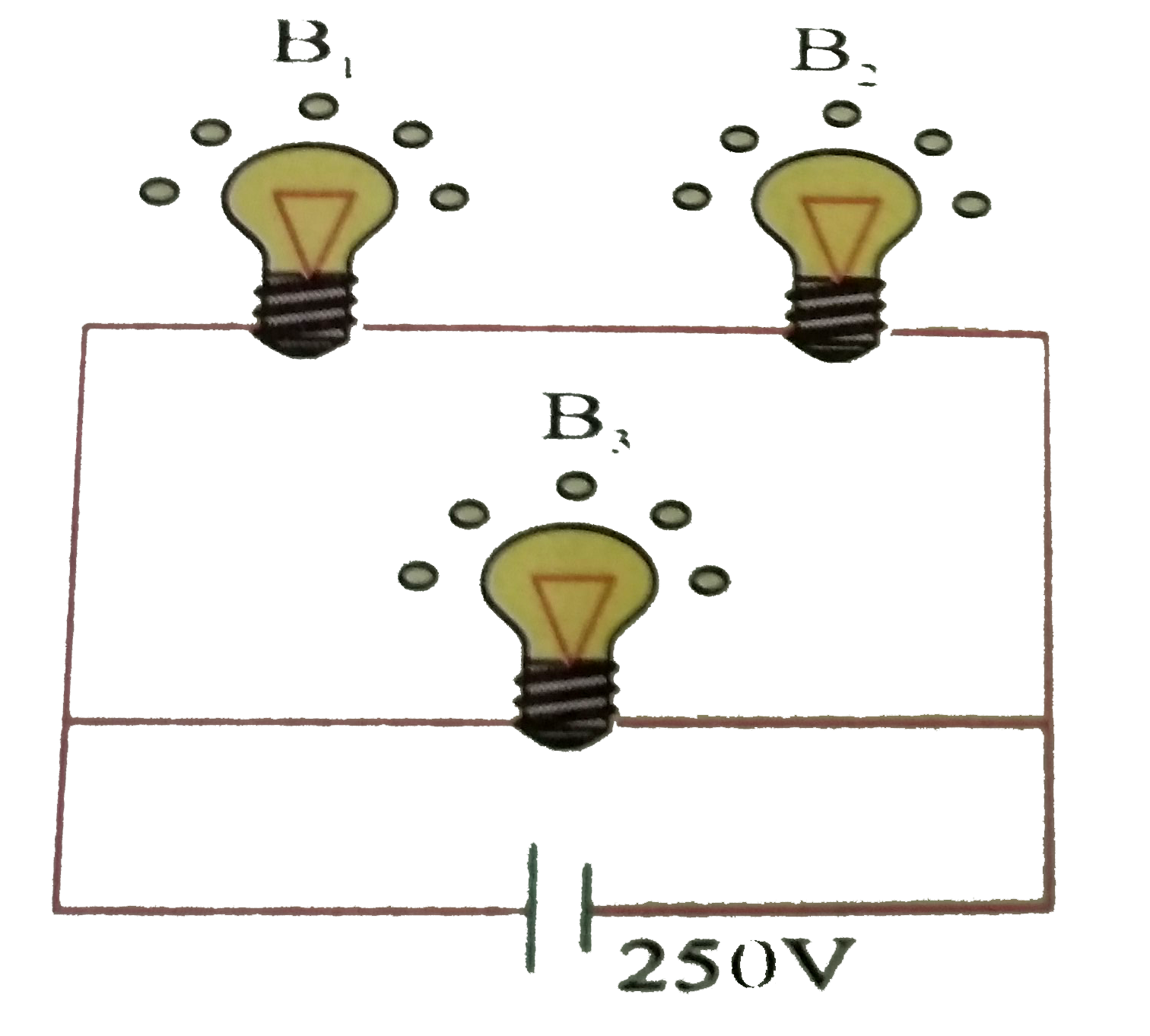
A 100 W bulb B1 and two 60 W bulbs B2 and B3, are connected to a 250V source, as shown in the figure now W1,W2 and W3 are the output powers of the bulbs B1,B2 and B3 respectively thenAW1>W2=W3BW1>W2>W3CW1<W2=W3DW1<W2<W3
A 100 W bulb B1 and two 60 W bulbs B2 and B3, are connected to a 250V source, as shown in the figure now W1,W2 and W3 are the output powers of the bulbs B1,B2 and B3 respectively thenAW1>W2=W3BW1>W2>W3CW1<W2=W3DW1<W2<W3
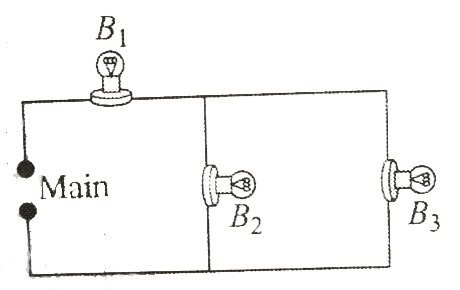
Three bulbs B1,B2andB3 are connected to the mains as shown in Fig. 7.28. How will the brightness of bulb B1 be affected B2orB3 are disconnected from the circuit?
View SolutionWhen two electric bulbs of 40W and 60W are connected in parallel, then the:
View SolutionBulb B1(100W−250V) and bulb B2(100W−200V) are connected across 250V. What is potential drop across B2 ?
View SolutionA 100W200V bulb is connected to a 160V power supply. The power consumption would be
View SolutionTwo bulbs 100W,250V and 200W,250V are connected in parallel across a 500V line. Then-
View SolutionThree electric bulbs of 200 W, 200 W and 400 W are connected as shown in figure. The resultant power of the combination is
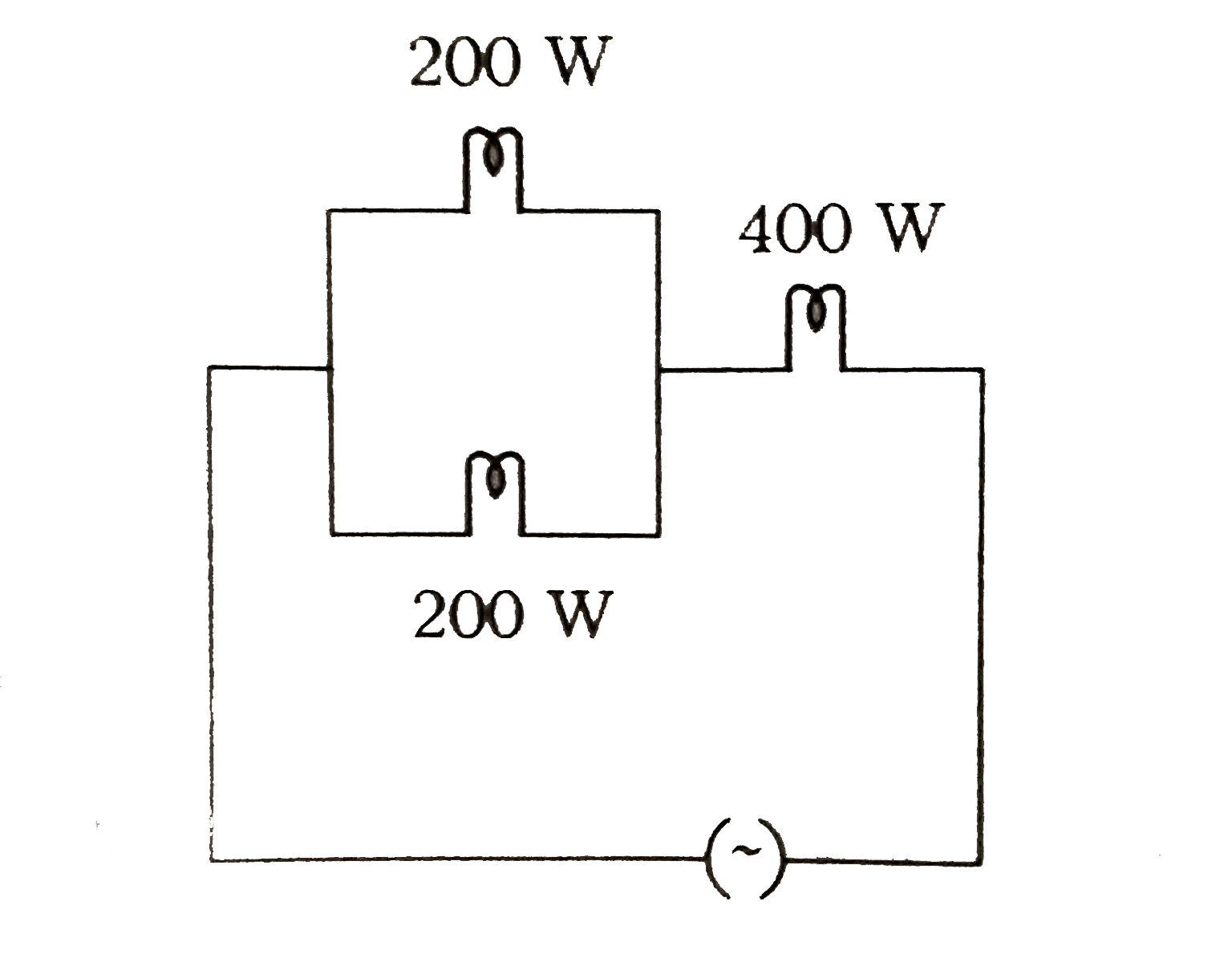
View Solution
