Two sources of equal emf are connected in series and having different internal resistance r1 and r2(r2>r1). Find the external resistance R at which the potential difference across the terminals of one of the sources becomes equal to zero.
V=E−ir
E and i for both the sources are equal. Therefore, potential difference (V) will be zero for a source having greater internal resistance i.e. r2
∴0=E−ir2
or E=ir2=(2ER+r1_r2).r2
∴2r2=R+r1+r2
or R=r2−r1
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise 23.16videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise 23.21videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Example Type 61videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective11videos
COMMUNICATION SYSTEM
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery25videos
ELECTROMAGNETIC INDUCTION
Similar Questions
If E is the emf of a cell of internal resistance r and external resistance R, then potential difference across R is given as
View Solution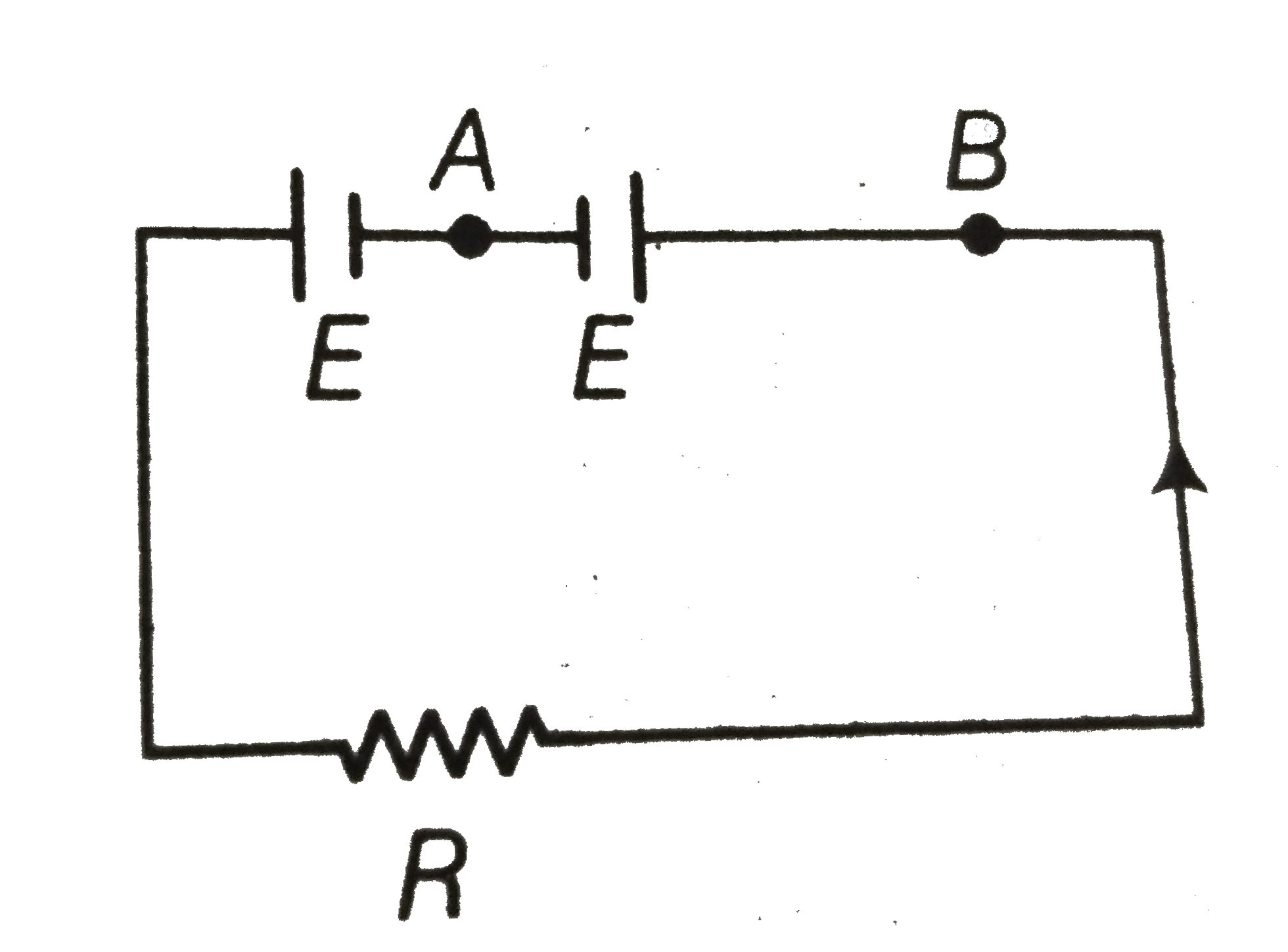
Two cells of same emf E but internal resistance r1andr2 are connected in series to an external resistor R(figure). What should be the value of R so that the potential difference across the terminals of the first cell becomes zero?View SolutionAccording to this diagram , the potential difference across the terminals is ( internal resistance of cell =r)
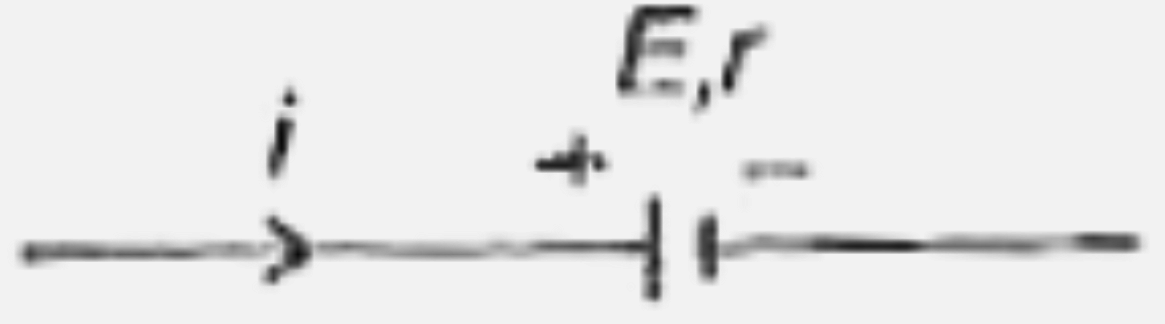 View Solution
View SolutionTwo cells of the same e.mf. e but different internal resistances r1andr2 are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris
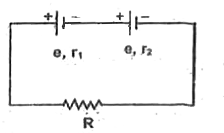 View Solution
View SolutionIn the given circuit, if the potential difference across the internal resistance r1 is equal to E, then the resistance R is equal to:
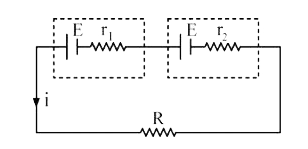 View Solution
View SolutionTwo cells, having the same emf, are connected in series through an external resistance R. Cells have internal resistance r1 and r2(r1>r2) respectively. When the circuit is closed, the potential difference across the first cell is zero the value of R is
View SolutionTwo cells, having the same emf, are connected in series through an external resistance R. Cells have internal resistance r1 and r2(r1>r2) respectively. When the circuit is closed, the potentail difference across the first cell is zero the value of R is
View SolutionTwo cells, having the same emf, are connected in series through an external resistance R. Cells have internal resistance r1 and r2(r1>r2) respectively. When the circuit is closed, the potentail difference across the first cell is zero the value of R is
View SolutionA capacitor is conneted to a cell emf E having some internal resistance r. The potential difference across the
View SolutionTwo sources of equal emf are connected to an external resistance R. The internal resistance of the two sources areR1andR2(R1>R1). If the potential difference across the source having internal resistance R2 is zero, then
View Solution

