A 1.5 kg steel sphere will not fit through a circular hole in a 0.85 kg aluminium plate, because the radius of the sphere is 0.10% larger than the radius of the hole. If both the sphere and the plate are always kept at the same temperature, how much heat must be put into the two so the ball just passes through the hole ?
6.2×104J
1.3×105J
7.0×104J
2.4×105J
The correct Answer is:B
To solve the problem, we need to determine how much heat must be added to both the steel sphere and the aluminum plate so that the sphere can pass through the hole in the plate. The key concept here is thermal expansion, which states that materials expand when heated.
1. Identify the Given Data:
- Mass of the steel sphere, ms=1.5kg
- Mass of the aluminum plate, ma=0.85kg
- Radius of the sphere is 0.10% larger than the radius of the hole.
2. Calculate the Difference in Radius:
- Let the radius of the hole be rh.
- The radius of the sphere rs=rh×(1+0.001)=1.001rh.
- The difference in radius Δr=rs−rh=0.001rh.
3. Convert the Difference in Radius to Diameter:
- The difference in diameter Δd=2Δr=2×0.001rh=0.002rh.
4. Thermal Expansion Formula:
- The change in diameter due to temperature change can be expressed as:
Δd=d0×α×ΔT
- Where d0 is the original diameter, α is the coefficient of linear expansion, and ΔT is the change in temperature.
5. Coefficients of Linear Expansion:
- Coefficient of linear expansion for aluminum, αa=24×10−6°C−1
- Coefficient of linear expansion for steel, αs=11×10−6°C−1
6. Calculate the Effective Change in Diameter:
- The effective change in diameter due to temperature change for both materials:
Δd=ΔT(αa−αs)×d0
- Rearranging gives:
ΔT=Δdd0(αa−αs)
7. Substituting Values:
- Assume d0 is the diameter of the hole.
- Substitute Δd=0.002rh, αa=24×10−6, and αs=11×10−6:
ΔT=0.002rhrh(24×10−6−11×10−6)
- Simplifying:
ΔT=0.00213×10−6≈153.85°C
8. Calculate Heat Required for Steel Sphere:
- Using Q=mcΔT:
- Specific heat of steel cs=480J/kg°C
- Heat required for steel sphere:
Qs=ms⋅cs⋅ΔT=1.5⋅480⋅153.85≈111,600J
9. Calculate Heat Required for Aluminum Plate:
- Specific heat of aluminum ca=900J/kg°C
- Heat required for aluminum plate:
Qa=ma⋅ca⋅ΔT=0.85⋅900⋅153.85≈117,000J
10. Total Heat Required:
- Total heat Qtotal=Qs+Qa:
Qtotal=111,600+117,000≈228,600J
Final Answer:
The total heat that must be put into the steel sphere and the aluminum plate so that the sphere just passes through the hole is approximately 228,600 Joules.
- Mass of the steel sphere, ms=1.5kg
- Mass of the aluminum plate, ma=0.85kg
- Radius of the sphere is 0.10% larger than the radius of the hole.
- Let the radius of the hole be rh.
- The radius of the sphere rs=rh×(1+0.001)=1.001rh.
- The difference in radius Δr=rs−rh=0.001rh.
- The difference in diameter Δd=2Δr=2×0.001rh=0.002rh.
- The change in diameter due to temperature change can be expressed as:
Δd=d0×α×ΔT
- Where d0 is the original diameter, α is the coefficient of linear expansion, and ΔT is the change in temperature.
- Coefficient of linear expansion for aluminum, αa=24×10−6°C−1
- Coefficient of linear expansion for steel, αs=11×10−6°C−1
- The effective change in diameter due to temperature change for both materials:
Δd=ΔT(αa−αs)×d0
- Rearranging gives:
ΔT=Δdd0(αa−αs)
- Assume d0 is the diameter of the hole.
- Substitute Δd=0.002rh, αa=24×10−6, and αs=11×10−6:
ΔT=0.002rhrh(24×10−6−11×10−6)
- Simplifying:
ΔT=0.00213×10−6≈153.85°C
- Using Q=mcΔT:
- Specific heat of steel cs=480J/kg°C
- Heat required for steel sphere:
Qs=ms⋅cs⋅ΔT=1.5⋅480⋅153.85≈111,600J
- Specific heat of aluminum ca=900J/kg°C
- Heat required for aluminum plate:
Qa=ma⋅ca⋅ΔT=0.85⋅900⋅153.85≈117,000J
- Total heat Qtotal=Qs+Qa:
Qtotal=111,600+117,000≈228,600J
The total heat that must be put into the steel sphere and the aluminum plate so that the sphere just passes through the hole is approximately 228,600 Joules.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - HEAT-MEASUREMENT AND TRANSFEREXERCISE - PRACTICE QUESTIONS(MORE THAN ONE CORRECT CHOICE TYPE )8videos
HEAT-MEASUREMENT AND TRANSFER
- BOOK - RESNICK AND HALLIDAYCHAPTER - HEAT-MEASUREMENT AND TRANSFEREXERCISE - PRACTICE QUESTIONS( LINKED COMPREHENSION)9videos
HEAT-MEASUREMENT AND TRANSFER
- BOOK - RESNICK AND HALLIDAYCHAPTER - HEAT-MEASUREMENT AND TRANSFEREXERCISE - PROBLEMS35videos
HEAT-MEASUREMENT AND TRANSFER
- BOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)4videos
GRAVITATION
- BOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PRACTICE QUESTIONS(Integer Type)6videos
HYDROGEN ATOM
Similar Questions
An iron ball has a diameter of 6cm and is 0.010mm too large to pass through a hole in a brass plate when the ball and plate are at a temperature of 30∘C. At what temperature, the same for ball and plate, will the ball just pass through the hole?
Take the values of (prop) from Table 20.2.View SolutionA circular hole in an aluminium plate has a diameter of 4cm at 0∘C. What is its diameter when the temperature of the plate is raised to 100∘C? (Linear expansivity of aluminium =23×10−6K−1)
View Solution
Knowledge Check
- Question 1 - Select One
An iron ball (coefficient of linear expansion=1.2×(10−5/∘C) has a diameter of 6 cm and is 0.010 mm too large to pass through a hole in a brass plate (coefficient of linear expansion=1.9×10−5/∘C) when the ball and the plate are both at a temperature of 30∘C At what common temperature of the ball and the plate will the ball just pass through the hole in the plate ?
A23.8∘CB53.8∘CC42.5∘CD63.5∘C - Question 2 - Select One or More
Two sphere of same radius and material, one solid and one hollow are heated to same temperature and kept in a chamber maintained at lower temperature at t = 0 -
ARate of heat loss of the two sphere will be same at t = 0BRate of temperature loss of the two sphere will be same at t = 0CRate of heat loss of solid sphere will be more than hollow sphere at t > 0DRate of temperature loss of the two sphere may be same at t > 0 - Question 3 - Select One
A steel ball of 50mm radius is kept on a hole of concrete. The diameter of the hole is 0.05mm less then the diameter of the steel ball at 20∘C. Coefficient of volume expansion of the steel ball is 3.2x10−6/∘C . At what temperature the ball will be inside the hole ?
A30∘CB55∘CC65∘CD70∘C
A solid aluminium sphere and a solid copper sphere of twice the radius are heated to the same temperature and are allowed to cool under identical surrounding temperature. Assume that the emissivity of both the spheres is the same. Find the ratio of
(a) the rate of heat from the aluminium sphere to the rate of heat loss from the copper sphere and
(b) the rate of fall of temperature of the the aluminium sphere to the rate of fall temperature of teh copper sphere. The specific heat capacity of aluminium =900J/kg−∘C and that of copper =390J/kg−∘C. The density of copper is 3.4 times the density of aluminium.View SolutionA table top is made of aluminium and has a hole of diameter 2 cm. An iron sphere of diameter 2.004 m is resting on this hole. Below the hole, an insulated container has 2 kg of water in it. Everything is at ambient temperature of 25∘C. The table top along with the iron sphere is heated till the ball falls through the hole into the water. Find the equilibrium temperature of the ball and water system
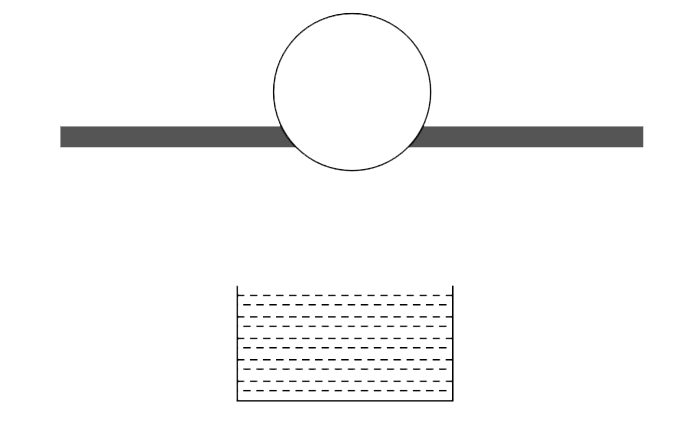
Neglect any heat loss from ball–water system to the surrounding and assume the heat capacity of the container to be negligible.
Relevant data: Coefficient of linear expansion for aluminium and iron are 2.4×10−5.∘C−1 and 1.2×10−5.∘C−1 respectively. Specific heat capacity of water and iron are 4200J.∘C−1g−1 and 450J.∘C−1g−1 respectively. Density of iron at 25∘C is 8000kg/m3.View SolutionVisible light passing through a circular hole forms a diffraction disc of radius 0.1 mm on a screen. If X-ray is passed through the same set-up, the radius of the diffraction disc will be
View SolutionA particle of mass 1kg is kept on the surface of a uniform sphere of mass 20kg and radius 1.0m. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
View SolutionA cylindrical steel plug is inserted into a circular hole of diameter 2.60 cm in a brass plate. When the plug and the plates are at a temperature of 20∘C, the diameter of the plug is 0.010 cm cmaller than that of the hole. The temperature at which the plug will just fit in it is
(Given,αsteel=11×10−6∘Candαbress=19×10−6C)View Solution

