A wide truck is moving with a uniform speed along a straight horizontal road. pedestrian starts to cross the road with a uniform speed when the truck is away from him, The minimum value of so that he can cross the road safely is .
The correct Answer is:C
To solve the problem, we need to determine the minimum speed v of the pedestrian so that he can cross the road safely before the truck reaches him. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the scenario
- The truck is 2 meters wide and is moving towards the pedestrian at a speed of v0=8m/s.
- The pedestrian starts crossing the road when the truck is 4 meters away from him.
Step 2: Calculate the time taken by the truck to reach the pedestrian
- The distance from the truck to the pedestrian is 4 meters.
- The speed of the truck is v0=8m/s.
- The time tt taken by the truck to reach the pedestrian can be calculated using the formula:
tt=DistanceSpeed=4m8m/s=0.5s
Step 3: Calculate the time required for the pedestrian to cross the road
- The pedestrian needs to cross a distance of 2 meters (the width of the truck).
- Let v be the speed of the pedestrian.
- The time tp taken by the pedestrian to cross the road can be expressed as:
tp=DistanceSpeed=2mv
Step 4: Set the times equal for safe crossing
- For the pedestrian to cross safely, the time taken by the truck to reach him must be equal to or greater than the time taken by the pedestrian to cross:
tt≥tp
Substituting the expressions we found:
0.5s≥2mv
Step 5: Solve for the pedestrian's speed v
- Rearranging the inequality gives us:
v≥2m0.5s=4m/s
Conclusion
- The minimum speed v of the pedestrian so that he can cross the road safely is:
v=4m/s
- The truck is 2 meters wide and is moving towards the pedestrian at a speed of v0=8m/s.
- The pedestrian starts crossing the road when the truck is 4 meters away from him.
- The distance from the truck to the pedestrian is 4 meters.
- The speed of the truck is v0=8m/s.
- The time tt taken by the truck to reach the pedestrian can be calculated using the formula:
tt=DistanceSpeed=4m8m/s=0.5s
- The pedestrian needs to cross a distance of 2 meters (the width of the truck).
- Let v be the speed of the pedestrian.
- The time tp taken by the pedestrian to cross the road can be expressed as:
tp=DistanceSpeed=2mv
- For the pedestrian to cross safely, the time taken by the truck to reach him must be equal to or greater than the time taken by the pedestrian to cross:
tt≥tp
Substituting the expressions we found:
0.5s≥2mv
- Rearranging the inequality gives us:
v≥2m0.5s=4m/s
- The minimum speed v of the pedestrian so that he can cross the road safely is:
v=4m/s
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - MCQ_TYPE27videos
KINEMATICS 1
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - COMPREHENSION_TYPE19videos
KINEMATICS 1
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE10videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery39videos
LAWS OF MOTION
Similar Questions
A man of height h is walking at constant speed v0 along edge of a straight horizontal road. There is a lamp post of height H=2h on the other edge as shown. If speed of tip of shadow of his head is nv0 then find n.
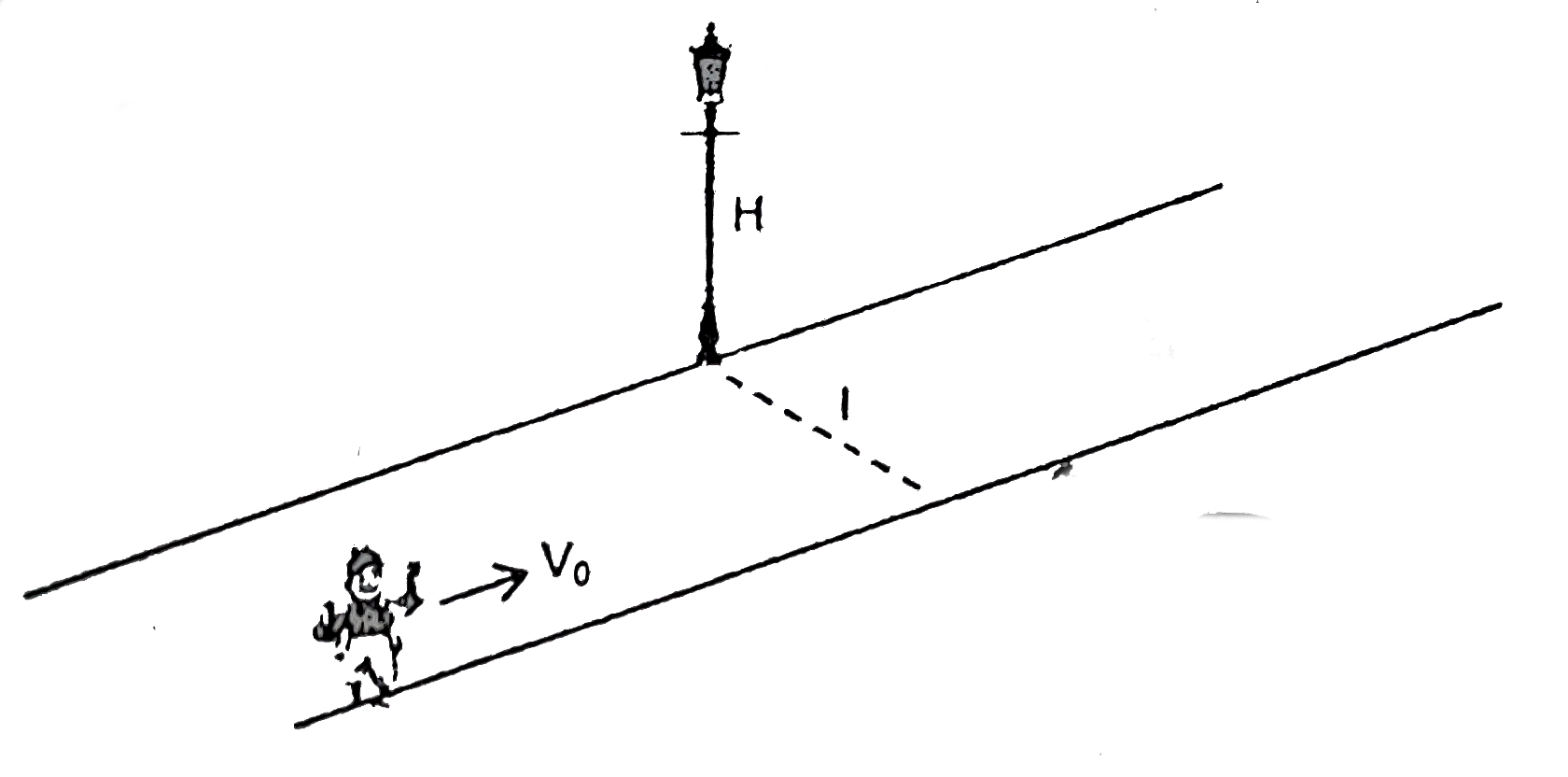 View Solution
View SolutionA body of mass 10 kg moves with a constant speed v of 2 ms−1 along a circular path of radius 8 m. The power produced by the body will be
View Solution
Knowledge Check
- Question 1 - Select One
A bus is moving with a speed of 10ms−1 on a straight road. A scooterist wishes to overtake the bus in 100 s. If the bus is at a distance of 1 km from the scooteritst with what speed should the scooterist chase the bus?
A40ms−1B25ms−1C10ms−1D20ms−1
A car is moving along a straight horizontal road with a speed v0 . If the coefficient of friction between the tyres and the road is μ , the shortest distance in which the car can be stopped is
View SolutionA body is moving with uniform velocity of 8ms−1. When the body just crossed another body, the second one starts and moves with uniform acceleration of 4ms−2. The time after which two bodies meet will be :
View SolutionA body is moving with uniform velocity of 8ms−1. When the body just crossed another body, the second one starts and moves with uniform acceleration of 4ms−2. The time after which two bodies meet will be :
View SolutionA car of mass M is moving with a uniform velocity υ on a horizontal road when the hero of a Hindi film drops himself on it from above. Taking the mass of the hero to be m what will be the velocity of the car after the event?
View SolutionA person is standing on a truck moving with a constant velocity of 14.7 m/s o a hrozontal road. The man throws a ball in such a way that it returns to the truck after the truck has moved 58.8 m. Find the speed and the angle of projection. a. as seen from the truck b. as seen fromt the road.
View SolutionTwo cars AandB are moving west to east and south to north, respectively, along crossroads. A moves with a speed of 20ms−1 and is 500m away from the point of intersection of cross roads and B moves with a speed of 15ms−1 and is 400m away from the point of intersection of cross roads. Find the shortest distance between them.
View SolutionA wheel of radius r rolls without slipping with a speed v on a horizontal road. When it is at a point A on the road, a small blob of mud separates from'the wheel at- its highest point and lands at point B on the road:
View Solution

