A 3000kg space probe is moving in a gravity free space at a constant velocity of 300m/s. To change the direction of space probe, rockets have been fired in a direction perpendicular to the direction of initial motion of the space probe, the rocket firing exerts a thrust of 4000N for 225s. The space probe will turn by an angle of (neglect the mass of the rockets fired)
30∘
60∘
45∘
37∘
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Identify the initial momentum of the space probe
The initial momentum (P_initial) of the space probe can be calculated using the formula:
Pinitial=m⋅vi
where:
- m=3000kg (mass of the space probe)
- vi=300m/s (initial velocity)
Calculating:
Pinitial=3000kg⋅300m/s=900000kg m/s
Step 2: Calculate the change in momentum due to the thrust
The change in momentum (P_thrust) caused by the thrust of the rockets can be calculated using:
Pthrust=F⋅t
where:
- F=4000N (thrust)
- t=225s (time duration)
Calculating:
Pthrust=4000N⋅225s=900000N s
Step 3: Apply conservation of momentum in the y-direction
When the rockets are fired, the momentum in the y-direction (P_y) will equal the change in momentum due to the thrust:
Py=Pthrust=900000kg m/s
Step 4: Apply conservation of momentum in the x-direction
The momentum in the x-direction (P_x) remains unchanged since there are no external forces acting in that direction:
Px=Pinitial=900000kg m/s
Step 5: Relate the momentum components to the angle θ
The momentum components can be expressed in terms of the angle θ:
- In the y-direction: Py=Psin(θ)
- In the x-direction: Px=Pcos(θ)
Where P is the resultant momentum after the thrust is applied.
Step 6: Set up the equations
From the conservation of momentum:
1. Psin(θ)=900000
2. Pcos(θ)=900000
Step 7: Divide the equations to find θ
Dividing the first equation by the second:
Psin(θ)Pcos(θ)=900000900000
This simplifies to:
tan(θ)=1
Step 8: Solve for θ
Taking the arctan of both sides:
θ=arctan(1)=45∘
Final Answer
The space probe will turn by an angle of 45∘.
---
The initial momentum (P_initial) of the space probe can be calculated using the formula:
Pinitial=m⋅vi
where:
- m=3000kg (mass of the space probe)
- vi=300m/s (initial velocity)
Pinitial=3000kg⋅300m/s=900000kg m/s
The change in momentum (P_thrust) caused by the thrust of the rockets can be calculated using:
Pthrust=F⋅t
where:
- F=4000N (thrust)
- t=225s (time duration)
Pthrust=4000N⋅225s=900000N s
When the rockets are fired, the momentum in the y-direction (P_y) will equal the change in momentum due to the thrust:
Py=Pthrust=900000kg m/s
The momentum in the x-direction (P_x) remains unchanged since there are no external forces acting in that direction:
Px=Pinitial=900000kg m/s
The momentum components can be expressed in terms of the angle θ:
- In the y-direction: Py=Psin(θ)
- In the x-direction: Px=Pcos(θ)
From the conservation of momentum:
1. Psin(θ)=900000
2. Pcos(θ)=900000
Dividing the first equation by the second:
Psin(θ)Pcos(θ)=900000900000
This simplifies to:
tan(θ)=1
Taking the arctan of both sides:
θ=arctan(1)=45∘
The space probe will turn by an angle of 45∘.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct25videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective23videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
Knowledge Check
- Question 1 - Select One
The force on a rocket moving with a veloctiy 300 m/s is 210N. The rate of consumption of fuel of rocket is
A0.07kgs−1B1.4kgs−1C0.7kgs−1D10.7kgs−1
DNA probe is used in
View SolutionThe electromagnetic waves travel in free space with the velocity of
View Solutiona charged particle moves in a gravity free space without change in velocity. Which of the following is/are possible?
View Solutiona charged particle moves in a gravity free space without change in velocity. Which of the following is/are possible?
View SolutionA rocket of mass 120kg. Is fired in the gravity free space is ejected gases with velocity 600 m/s at the rate of 1kg/s. what will be the initial accleration of the rocket:-
View SolutionA metal rod moves at a constant velocity in a direction perpendicular to its length. A constant, uniform magnetic field exists in space in a direction perpendicular to the rod as well as its velocity. Select the correct statements(s) from the following
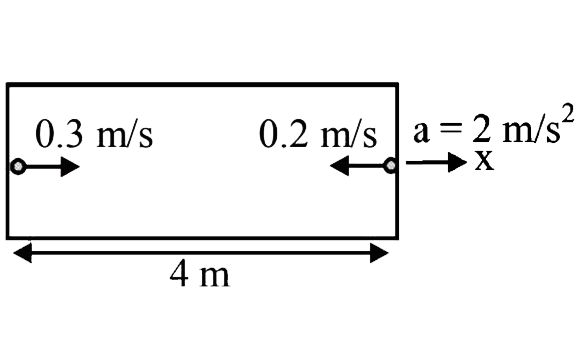
View SolutionA rocket is moving in a gravity free space with a constant acceleration of 2m/s2 along +x direction (see figure). The length of a chamber inside the rocket is 4m. A ball is thrown from the left end of the chamber in +x direction with a speed of 0.3m/s relative to the rocket . At the same time , another ball is thrown in +x direction with a speed of 0.2m/s drom its right end relative to the rocket . The time in seconds when the two balls hit each other is
 View Solution
View Solution

