A parallel beam of particles each of mass m moving with velocity v impinges on a wall at an angle θ to its normal. The number of particles per unit volume in the beam is n. If the collision of particles with the wall is elastic, then the pressure exerted by this beam on the wall is
2mnv2cosθ
2mnv2cos2θ
2mnvcosθ
2mnvcos2θ
The correct Answer is:B
To find the pressure exerted by a parallel beam of particles on a wall, we will follow these steps:
Step 1: Understand the problem
We have a beam of particles, each of mass m, moving with a velocity v at an angle θ to the normal of a wall. The number of particles per unit volume in the beam is n. The collisions with the wall are elastic, meaning the particles will bounce back with the same speed but in the opposite direction.
Step 2: Resolve the velocity into components
The velocity v can be resolved into two components:
- The component perpendicular to the wall (normal component): vcosθ
- The component parallel to the wall (tangential component): vsinθ
Step 3: Calculate the change in momentum
When a particle strikes the wall, it reverses its normal component of velocity. The change in momentum Δp for one particle can be calculated as:
Δp=m(vcosθ−(−vcosθ))=2mvcosθ
Step 4: Determine the number of particles striking the wall
The volume dV of the beam of particles striking the wall can be expressed as:
dV=dA⋅dx⋅cosθ
where dA is the area of the wall and dx is the thickness of the beam.
The number of particles dN in this volume is:
dN=n⋅dV=n⋅dA⋅dx⋅cosθ
Step 5: Calculate the total change in momentum for all particles
The total change in momentum for all particles striking the wall is:
ΔP=dN⋅Δp=(n⋅dA⋅dx⋅cosθ)⋅(2mvcosθ)
Substituting the expression for dN:
ΔP=2mnvcos2θ⋅dA⋅dx
Step 6: Calculate the force exerted on the wall
The force F exerted on the wall is the rate of change of momentum. If dt is the time taken for the particles to strike the wall, we can express the force as:
F=ΔPdt
The distance dx can be expressed as v⋅dt, hence:
F=2mnvcos2θ⋅dA⋅v⋅dtdt=2mnv2cos2θ⋅dA
Step 7: Calculate the pressure
Pressure P is defined as force per unit area:
P=FdA=2mnv2cos2θ⋅dAdA=2mnv2cos2θ
Final Answer
The pressure exerted by the beam of particles on the wall is:
P=2mnv2cos2θ
---
We have a beam of particles, each of mass m, moving with a velocity v at an angle θ to the normal of a wall. The number of particles per unit volume in the beam is n. The collisions with the wall are elastic, meaning the particles will bounce back with the same speed but in the opposite direction.
The velocity v can be resolved into two components:
- The component perpendicular to the wall (normal component): vcosθ
- The component parallel to the wall (tangential component): vsinθ
When a particle strikes the wall, it reverses its normal component of velocity. The change in momentum Δp for one particle can be calculated as:
Δp=m(vcosθ−(−vcosθ))=2mvcosθ
The volume dV of the beam of particles striking the wall can be expressed as:
dV=dA⋅dx⋅cosθ
where dA is the area of the wall and dx is the thickness of the beam.
dN=n⋅dV=n⋅dA⋅dx⋅cosθ
The total change in momentum for all particles striking the wall is:
ΔP=dN⋅Δp=(n⋅dA⋅dx⋅cosθ)⋅(2mvcosθ)
Substituting the expression for dN:
ΔP=2mnvcos2θ⋅dA⋅dx
The force F exerted on the wall is the rate of change of momentum. If dt is the time taken for the particles to strike the wall, we can express the force as:
F=ΔPdt
The distance dx can be expressed as v⋅dt, hence:
F=2mnvcos2θ⋅dA⋅v⋅dtdt=2mnv2cos2θ⋅dA
Pressure P is defined as force per unit area:
P=FdA=2mnv2cos2θ⋅dAdA=2mnv2cos2θ
The pressure exerted by the beam of particles on the wall is:
P=2mnv2cos2θ
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A parallel beam of particles each of mass m moving with velocity v impinges on a wall at an angle θ to its normal. The number of particles per unit volume in the beam is n. If the collision of particles with the wall is elastic, then the pressure exerted by this beam on the wall is
View SolutionA molecule of mass m moving at a velocity v impinges elastically on the wall at an angle α with the wall. Then
View Solution
Knowledge Check
A particle A with a mass mA is moving with a velocity v and hits a particle B (mass mB) at rest (one dimensional motion). Find the change in the de-Broglie wavelength of the particle A. Treat the collision as elastic.
Ah2mAv[(mA+mB)(mA−mB)−1]BhmAv[(mA−mB)(mA+mB)−1]ChmAv[(mA+mB)(mA−mB)−1]D2hmAv[(mA+mB)(mA−mB)+1]
A particle of mass m is projected with a velocity v at an angle of θ with horizontal. The angular momentum of the particle at the highest point of its trajectory is equal to :
View SolutionA particle of mass m is moving with constant velocity v parallel to the x-axis as shown in the figure. Its angular momentum about origin O is

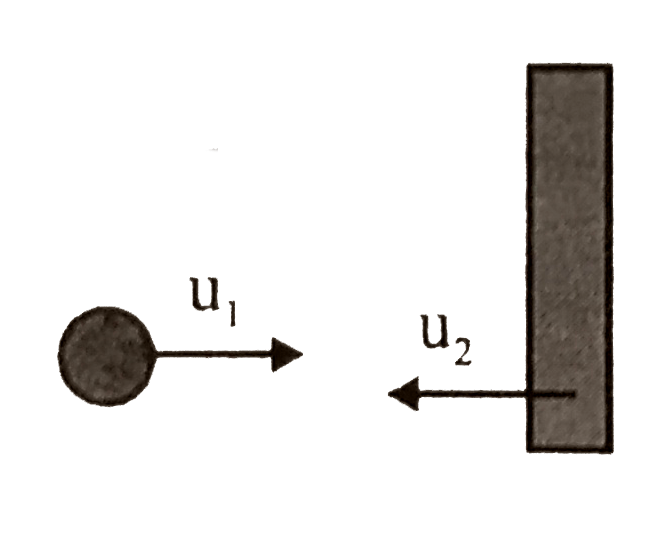
View SolutionA particle of mass m moves with velocity u1=20m/s towards a wall that is moving with velocity u2=5m/s. If the particle collides with the wall without losing its energy, find the speed of particle just after the collision.
View SolutionA particle of mass m moving at a velocity v strikes with the wall at an angle α with the wall and leaves ball making same angle with the wall. Choose the correct statemet (s) from the following.
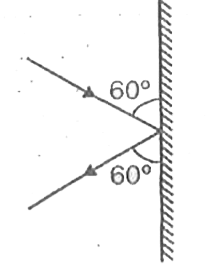
View SolutionA body of mass 3 kg moving with velocity 10 m/s hits a wall at an angle of 60∘ and returns at the same angle. The impact time was 0.2 s. Calculate the force exerted on the wall.
View SolutionA particle A with a mass mA is moving with a velocity v and hits a particle B (mass mB) at rest (one dimensional motion). Find the change in the de-Broglie wavelength of the particle A. Treat the collision as elastic.
View SolutionA particle of mass m moving with velocity v makes head-on elastic collision with a sationary particle of mass 2m. Kinetic energy lost by the lighter particle during period of deformation is
View Solution
