A 3.0kg block has a speed of 2m/s A and 6m/s at B. If the distance from A and B along the curve is 12m, how large a frictional force acts on it ? Assuming the same friction, how far from B will it stop ?
To solve the problem step by step, we will follow the principles of work and energy.
Step 1: Identify the Given Data
- Mass of the block (m) = 3.0 kg
- Speed at point A (Va) = 2 m/s
- Speed at point B (Vb) = 6 m/s
- Distance along the curve from A to B (S) = 12 m
Step 2: Calculate the Change in Kinetic Energy
The change in kinetic energy (ΔKE) can be calculated using the formula:
ΔKE=KEfinal−KEinitial=12mV2b−12mV2a
Substituting the values:
ΔKE=12×3×(62)−12×3×(22)
=12×3×36−12×3×4
=54−6=48 J
Step 3: Calculate the Change in Potential Energy
Assuming the height at point A (hA) is 4 m and at point B (hB) is 1 m, the change in potential energy (ΔPE) is given by:
ΔPE=PEfinal−PEinitial=mghB−mghA
Substituting the values:
ΔPE=3×9.8×1−3×9.8×4
=29.4−117.6=−88.2 J
Step 4: Calculate Work Done by Friction
According to the work-energy principle:
ΔKE=Wgravity+Wfriction
Where Wgravity=−ΔPE. Thus:
Wfriction=ΔKE+ΔPE
Substituting the values:
Wfriction=48+(−88.2)=−40.2 J
Step 5: Relate Work Done by Friction to Frictional Force
The work done by friction can also be expressed as:
Wfriction=F⋅S⋅cos(180∘)
Since cos(180∘)=−1:
−40.2=F⋅12⋅(−1)
F=40.212=3.35 N
Step 6: Calculate the Distance from B to Stop
Now, we need to calculate how far the block will travel from point B until it stops. At point C (where it stops), the kinetic energy is zero. Thus:
Wfriction=ΔKE+ΔPE
Where:
- KEB=12mV2b=48 J
- PEC=0
- PEB=mghB=3×9.8×1=29.4 J
Now, substituting these into the equation:
−F⋅S′=0−48+29.4
−F⋅S′=−18.6
3.35⋅S′=18.6
S′=18.63.35≈5.56 m
Final Answers
1. The frictional force acting on the block is 3.35 N.
2. The distance from point B to where the block stops is approximately 5.56 m.
- Mass of the block (m) = 3.0 kg
- Speed at point A (Va) = 2 m/s
- Speed at point B (Vb) = 6 m/s
- Distance along the curve from A to B (S) = 12 m
The change in kinetic energy (ΔKE) can be calculated using the formula:
ΔKE=KEfinal−KEinitial=12mV2b−12mV2a
Substituting the values:
ΔKE=12×3×(62)−12×3×(22)
=12×3×36−12×3×4
=54−6=48 J
Assuming the height at point A (hA) is 4 m and at point B (hB) is 1 m, the change in potential energy (ΔPE) is given by:
ΔPE=PEfinal−PEinitial=mghB−mghA
Substituting the values:
ΔPE=3×9.8×1−3×9.8×4
=29.4−117.6=−88.2 J
According to the work-energy principle:
ΔKE=Wgravity+Wfriction
Where Wgravity=−ΔPE. Thus:
Wfriction=ΔKE+ΔPE
Substituting the values:
Wfriction=48+(−88.2)=−40.2 J
The work done by friction can also be expressed as:
Wfriction=F⋅S⋅cos(180∘)
Since cos(180∘)=−1:
−40.2=F⋅12⋅(−1)
F=40.212=3.35 N
Now, we need to calculate how far the block will travel from point B until it stops. At point C (where it stops), the kinetic energy is zero. Thus:
Wfriction=ΔKE+ΔPE
Where:
- KEB=12mV2b=48 J
- PEC=0
- PEB=mghB=3×9.8×1=29.4 J
−F⋅S′=0−48+29.4
−F⋅S′=−18.6
3.35⋅S′=18.6
S′=18.63.35≈5.56 m
1. The frictional force acting on the block is 3.35 N.
2. The distance from point B to where the block stops is approximately 5.56 m.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Conceptual Problems
27 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Very Short Anwer Question.
54 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Curiosity questions
2 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
A ball moves along a curved path of radius 5m as shown in figure. It starts from point A and reaches the point B. Calculate the normal force that acts on the ball at B, assuming that there is no friction between the ball and the surface of contact.
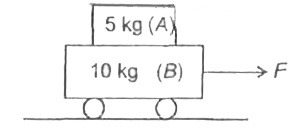
View SolutionIf acceleration of A is 2m/s2 which is smaller than acceleration of B then the value of frictional force applied by B on A is
View Solution
Knowledge Check
A turn of radius 20m is banked for the vehicle of mass 200kg going at a speed of 10m/s. Find the direction and magnitude of frictional force (a) 5m/s
(b) 15m/s
Assume that friction is sufficient to prevent slipping. (g=10m/s2)Af=200√5N (down wards)Bf=500√5N (up wards)Cf=500√5N (down wards)Df=200√5N (up wards)Two blocks A and B of masses mA and mB have velocity v and 2v respectively at a given instant A horizontal force F acts on the block A There is no friction between ground and block B and coefficient of friction between A and B is μ The friction
 Aon A supports its motionBon B opposes its motion relative to ACon B oppose its motionDoppose the motion of both
Aon A supports its motionBon B opposes its motion relative to ACon B oppose its motionDoppose the motion of bothA body of mass m kg starts from rest and travels a distance of s m in t seconds. The force acting on it is
A2mst2NBmstNCms22tNDms2tN
A turn of radius 100 m is banked for a speed of 20 m/s
(a) Find the banking angle
(b) If a vehicle of mass 500 kg negotiates the curve find the force of friction on it if its speed is – (i) 30 m/s (ii) 10 m/s
Assume that friction is sufficient to prevent skidding and slipping.
[Take tan22∘=0.4,sin22∘=0.375,cos22∘=0.93,g=10ms−2]
View SolutionA plank of mass 10kg rests on a smooth horizontal surface. Two blocks A and B of masses mA=2kgandmB=1kg lies at a distance of 3m on the plank as shown in the distance of 3m on the plank as shown in the figure. The friction coefficient between the blocks and plank are μA=0.3andμB=0.1. Now a force F = 15 N is applied to the plank in horizontal direction. Find the time after which block A collides with B.
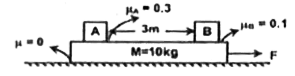
View SolutionA block weighing 20 N rests on a horizontal surface. The: coefficient of static friction between block and surface is 0.40 and the coefficient of kinetic friction is 0.20.
( a) How large is the friction force exerted on the block?
(b) How great will the friction force be if a horizontal force of 5 N is exerted on the block?
(c) What is the minimum force that will start the block in motion?
(d) What is the minimum force that will keep the block in motion once it has been started?
(e) If the horizontal force is 10 N, what is the friction force?
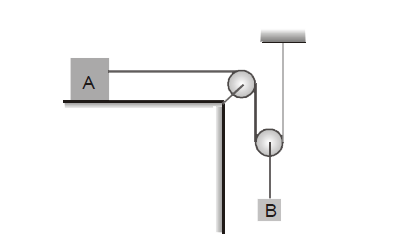
View SolutionIn the arrangement shown in figure mA = 4.0 kg and mB = 1.0 kg. The system is released from rest and block B is found to have a speed 0.3 m/s after it has descended through a distance of 1m. Find the coefficient of friction between the block and the table. Neglect friction elsewhere.
(Take g = 10 m/s2)
View SolutionA constant force acting on a block of mass 5 kg changes (a) its speed from 6m/s to 10m/s in travelling a distance 8m in a straight line, (b) its speed from 2m/s to 8m/s in 3s a straight line. Find the magnitude and the direction of the force.
View Solution