A $3 m$ along ladder weighing $20 k g$ leans on a frictionless wall. Its feet rest on the floor $1 m$ from the wall. Find the rection forces of the wall and the floor.

Video Solution

Text Solution

Verified by Experts

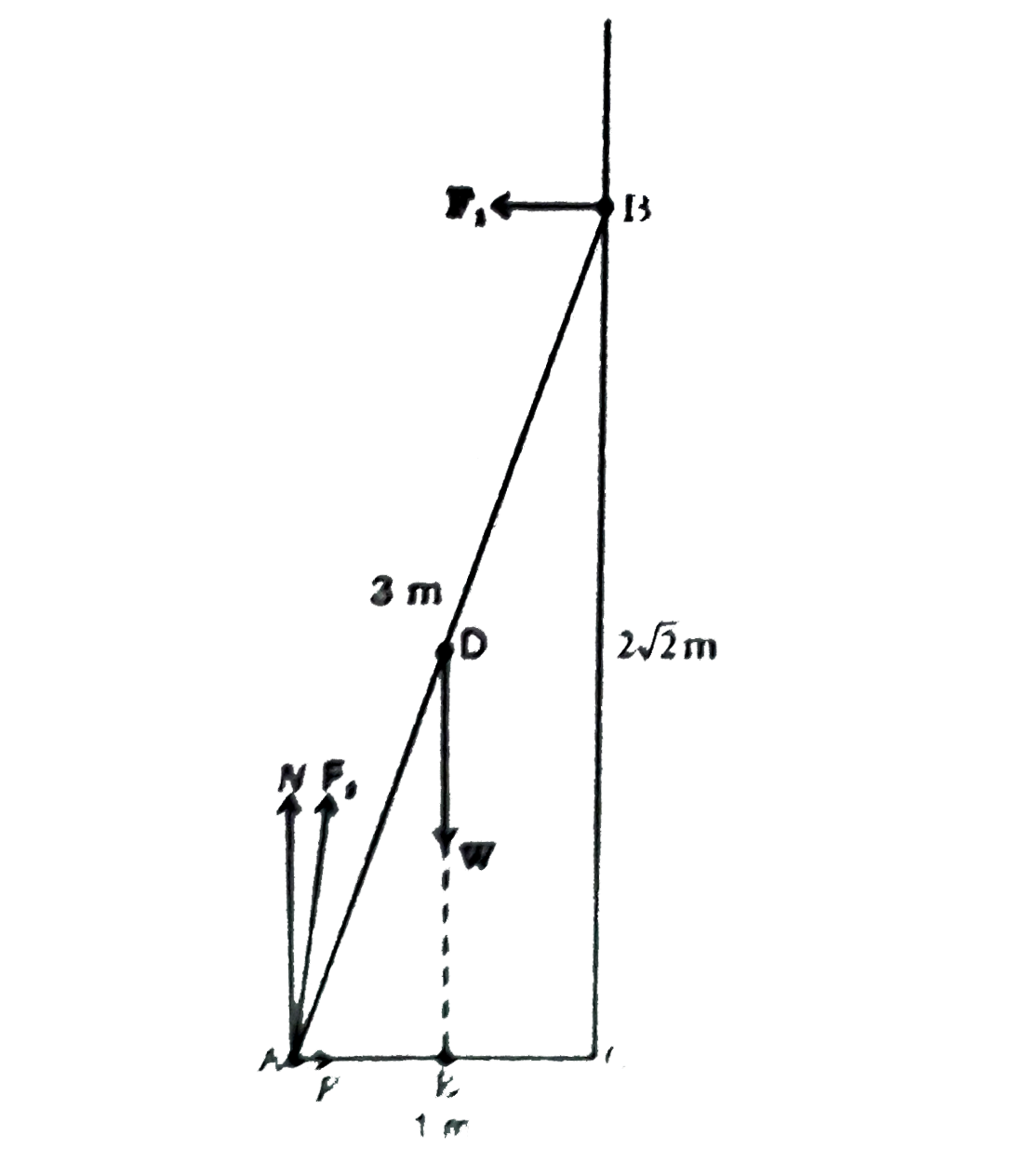
The ladder AB is 3 m long, its foot A is at distance AC=1 m from the wall. From
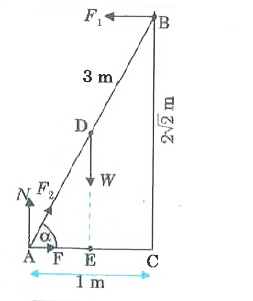
Pythagoras theorem, $B C = 2 \sqrt{2}$ m. The forces on the ladder are its weight W acting at its centre of gravity D, reaction forces $F_{1} and F_{2}$ of the wall and the floor respectively . Force $F_{1}$ is perpendicular to the wall, since the wall is frictionless. Force $F_{2}$ is resolved into two components, the normal reaction N and the components, the normal reaction N and the force of friction F. Not that F prevents the ladder from sliding away from the wall and is therefore directed toward the wall.
For translational equilibrium, taking the forces in the vertical direction,
N-W=0
Taking the forces in the horizontal direction,
$F - F_{1} = 0$
For rotational equilibrium, taking the moments of the forces about A,
$2 \sqrt{2} F_{1} - (1 / 2) W = 0$
Now $W = 20 g = 20 \times 9.8 N = 196.0 N$
From (i) N=196.0 N
From (iii) $F_{1} = W / 4 \sqrt{2} = 196.0 / 4 \sqrt{2} = 34.6 N$
From (ii) $F = F_{1} = 34.6 N$
$F_{2} = \sqrt{F^{2} + N^{2}} = 199.0 N$
The force $F_{2}$ makes an angle $α$ with the horizontal.
$tan α = N / F = 4 \sqrt{2}, α = {tan}^{- 1} (4 \sqrt{2}) \approx 80^{\circ}$ .

Updated on:21/07/2023