A car weighs 1800kg. The distance between its front and back axles is 1.8m. Its centre of gravity is 1.05m behind the front axle. Determine the force exerted by the level ground on each front wheel and each back wheel.
Let F1 and F2 be the forces exerted by the level ground on front wheels and back wheels respectively. Considering rotational equilibrium about the front wheels, F2×1.8=mg×1.05 or F2=1.05/1.8×1800×9.8N=10290N Force on each back wheel is 10290/2 N or 5145 N.
Considering rotational equilibrium about the back wheels.
F1×1.8=mg(1.8−1.05)=0.75×1800×9.8 or F1=0.75×1800×9.8/1.8=7350N
Force on each front wheel is 7350/2N or 3675 N.
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISE33videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - NCERTCHAPTER - PHYSICAL WORLD EXERCISE - EXERCISE16videos
PHYSICAL WORLD
- BOOK - NCERTCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXERCISE22videos
THERMAL PROPERTIES OF MATTER
Similar Questions
A car weighs 1800 kg. The distance between its front and back axles is 1·8 m. Its centre of gravity is 1·05 m behind the front axle. Determine the force exerted by the level ground on each front and back wheel
View SolutionA car weighs 1800kg. The distance between its front and back axles is 1.8m. Its centre of gravity is 1.05m behind the front axle. Determine the force (in newton) exerted by the level ground on each front wheel.
View Solution
Knowledge Check
- Question 1 - Select One
A car weighs 1800 kg. The distance between its front and back axles is 1.8 m. Its centre of gravity is 1 m behind the front axle. The force exerted by the level ground on each front wheel and each back wheel is (Take g:10ms−1)
A4000 N on each front wheel, 5000 N on each back wheelB5000 N on each front wheel, 4000 N an each back wheelC4500N on each front wheel, 4500 N on each back wheelD3000 N on each front wheel, 6000 N on each back wheel - Question 2 - Select One or More
The centre of gravity of a car is at a height h and the distance between its wheel is 2a. The car moves on a level curve of radius r with speed v. Let N1andN2 be the normal reactions on the inner and outer wheels of the car. Then
AN1>N2BN2>N1CN1=N2Dthe maximum value of v to avoid overturning is √argh - Question 3 - Select One
The tricycle weighing 20 kg has a small wheel symmmetrically placed 1m behind the two large wheels, which are also 1m apart. If the center of gravity of machine is at a horizontal distance of 25 cm behind the front wheels and the rider whose weight is 40 kg is 10 cm behind the front wheels. Then, the thrust on each front wheel is
A255 NB90 NC200 ND400 N
The radius of the front and rear wheels of a carriage are a and b, and c is the distance between the front an drear axles. A particle of dust driven from the highest point of the rear wheel is observed to alight on the highest point of the front wheel. Find the velocity of the carriage.
View SolutionThere is a man of mass 100 kg sitting on a motorbike of mass 150 kg. The distance of the axles of the wheels (wheelbase) is 1 . 5 m, the common mass center of the man and the motorbike is at a 1 m height above the ground level, and at a 0.6 m distance from the vertical line going through the rear axle.
What acceleration is needed to lift the front wheel?
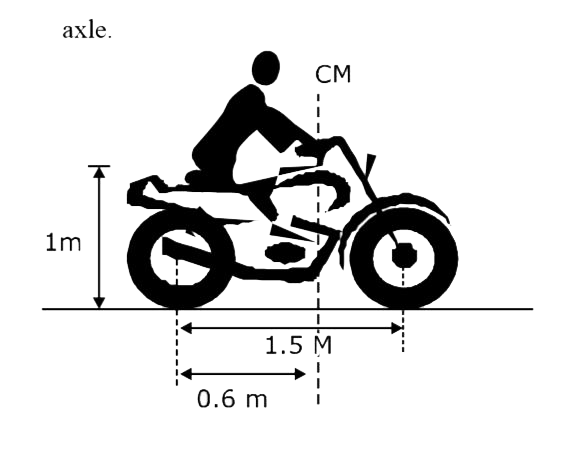 View Solution
View SolutionThere is a man of mass 100 kg sitting on a motorbike of mass 150 kg. The distance of the axles of the wheels (wheelbase) is 1 . 5 m, the common mass center of the man and the motorbike is at a 1 m height above the ground level, and at a 0.6 m distance from the vertical line going through the rear axle.
What acceleration is needed to lift the front wheel?
 View Solution
View SolutionWhat must be the minimum coefficient of friction μ between the tyres of the drive wheels of a car and the road, if the car and the road, if the car of mass m=2 tons and load M=4 tons, has an acceleration a=0.2ms−2 ? Consider the problem for two cases : (a) all the wheels are driven , (b) only the rear wheels are driven. Assume that the centre of gravity of the car lies at the mid-point between the axes of the wheel and the centre of gravity of the load above the rear axle.
View SolutionA motor car has a width 1.1m between wheels. Its centre of gravity is 0.62 m above the ground and the coefficient of friction between the wheels and the road is 0.8. What is the maximum possible speed, if the centre of gravity inscribes a circle of radius 15 m ? (Road surface is horizontal)
View Solution

