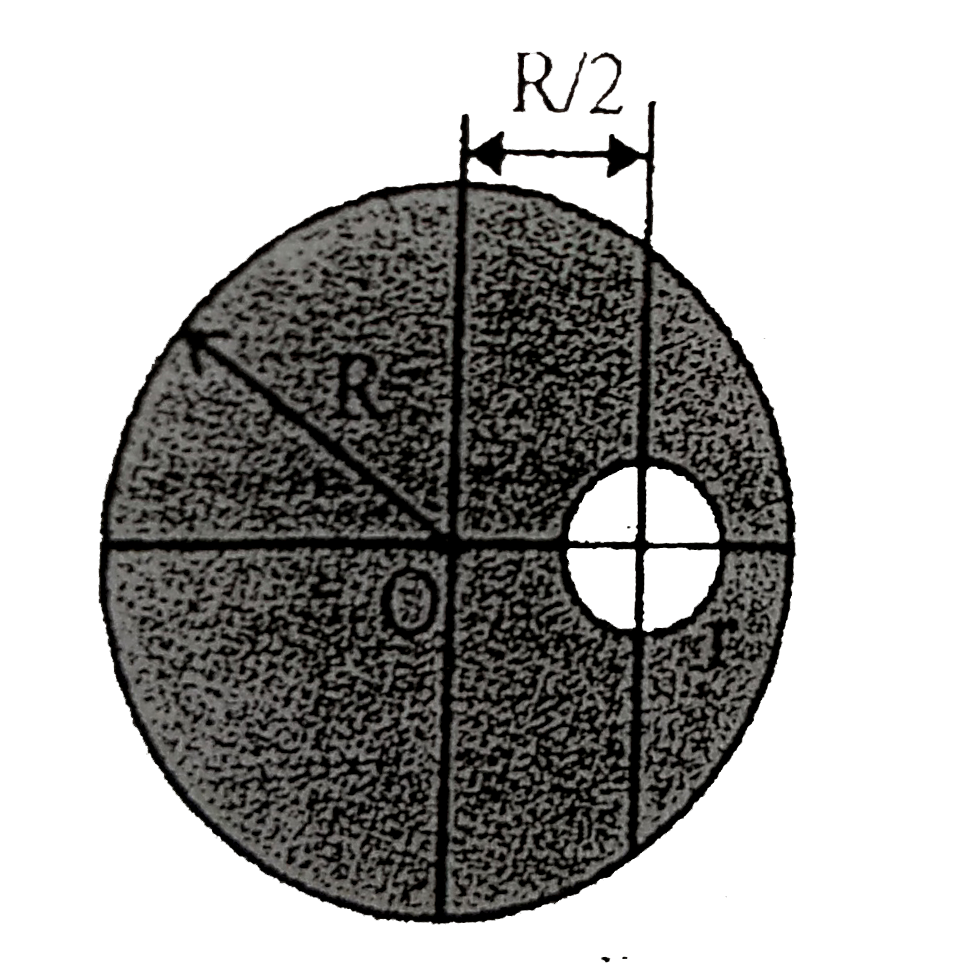
From a uniform disc of radius $R$ , a circular section of radius $R / 2$ is cut out. The centre of the hole is at $R / 2$ from the centre of the original disc. Locate the centre of mass of the resulting flat body.

Video Solution

Text Solution

Verified by Experts

Let from a bigger uniform disc of radius R with centre O a smaller circular hole of radius $R / 2$ with its centre at $O_{1}$ (where R $O O_{1} = R / 2)$ is cut out. Let centre of gravity or the centre of mass of remaining flat body be at $O_{2}$ , where $O O_{2} = x$ . If $σ$ be mass per unit area, then mass of whole disc $M_{1} = T T R^{2} σ$ and mass of cut out part
$M_{2} = π {(\frac{R}{2})}^{2} σ = \frac{1}{4} π R^{2} σ = \frac{M_{1}}{4}$
$x = \frac{M_{1} \times (0) - M_{2} (O O_{1})}{M_{1} - M_{2}} = \frac{0 - \frac{M_{1}}{4} \times \frac{R}{2}}{M_{1} - \frac{M_{1}}{4}} = - \frac{R}{6}$
i.e., $O_{2}$ is at a distnce $R / 6$ from centre of disc on diametrically opposite side to centre of hole.

Updated on:21/07/2023