A 4m long ladder weighing 25kg rests with its upper end against a smooth wall and lower end on rough ground.What should be the minimum coefficient of friction between the ground and the ladder for it to be inclined at 60∘ with the horizontal without slipping? (Takeg=10m/s2)
In figure, AB is a ladder of weight w which acts at its centre of gravity G.
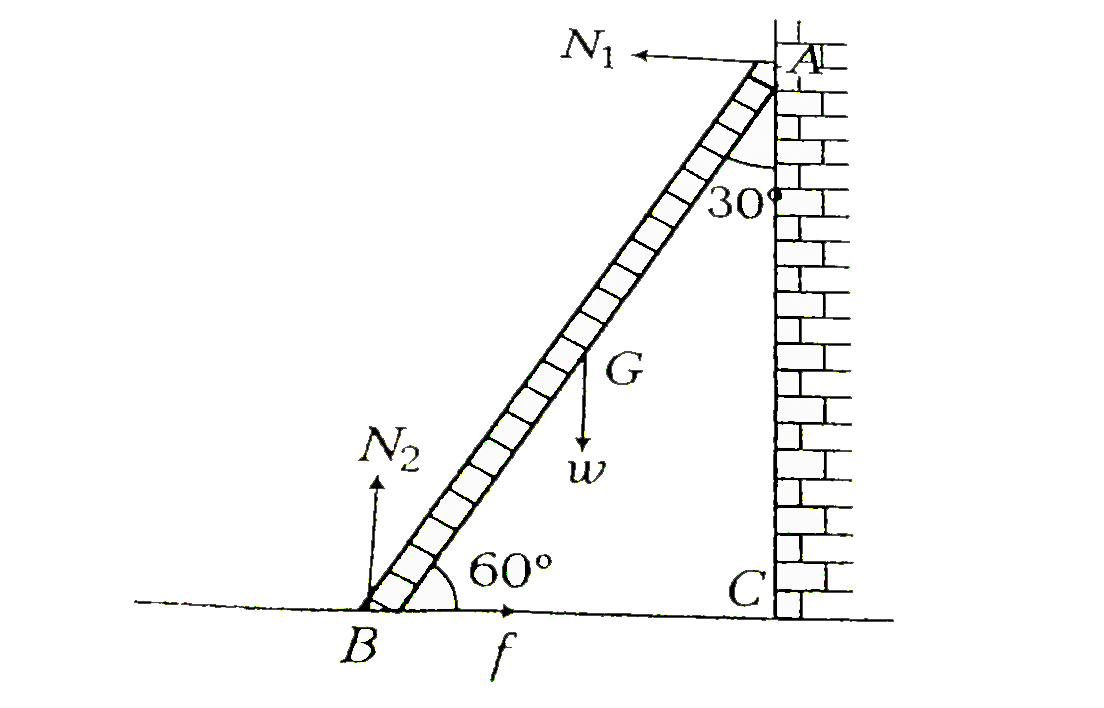
∠(ABC)=60∘∴∠(BAC)=30∘
Let N1 be the reaction of the wall, and N2 the reaction of the ground.
Force of friction f between the ladder and the ground acts along BC.
For horizontal equilibrium , f=N1.........(i)
For vertical equilibrium, N2=w ..........(ii)
Taking moments about B, we get for equilibrium,
N1(4cos30∘)−w(2cso60∘)=0.......(iii)
Here, w=250N
Solving these three equations , we get
f=72.17 Nand N2=250N
∴μ=fN2=72.17250=0.288
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.1
20 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.2
15 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Subjective Question
27 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A4m long ladder weighing 25kg rests with its upper and against a smooth wall and lower and on rought ground.What should be the minimum coefficient of friction between the ground and ladder for it to be inclined at 60∘ with the horizontal without slipping? (Takeg=10m/s2)
View SolutionA uniform rod of length L rests against a smooth roller as shown in figure. Find the friction coefficient between the ground and the lower end if the minimum angle that rod can make with the horizontal is θ.

View Solution
Knowledge Check
A car goes on a circular horizontal road of radius 100 m. What should be the minimum coefficient of friction between the tyres and the road so that it completes the circle with velocity 10 m/s without slipping ? (Take g=10m/s2)
A0.1B0.2C0.15D1A ladder of mass 10kg is held at reat against a smooth wall on a rough ground as shown in figure. The normal reaction between the wall and the ladder is
 A50NB50√3NC60√3ND100N
A50NB50√3NC60√3ND100NA ladder of length l and mass m is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is μ. The angle θ at which the ladder will stay in equilibrium is
Aθ=tan−1(μ)Bθ=tan−1(2μ)Cθ=tan−1(μ2)Dnone of these
A uniform rod of length L rests against a smooth roller as shown in figure. Find the friction coefficient between the ground and the lower end if the minimum angle that rod can make with the horizontal is θ.

View SolutionA ladder is kept at rest with is upper end against a wall and the lower end on the ground. The ladder is more like to slip when a mass stands on it at the top than at the bottom. Why ?
View SolutionA uniform ladder is placed against a wall, if the ground and wall are equally rough the coefficient of friction being tanθ limiting inclination of the ladder to the vertical is 2θ.
View SolutionA ladder of length 5m is placed against a smooth wall as shown in figure. The coefficient or friction is μ between ladder and ground. What is the minimum value of μ , If the ladder is not to slip?

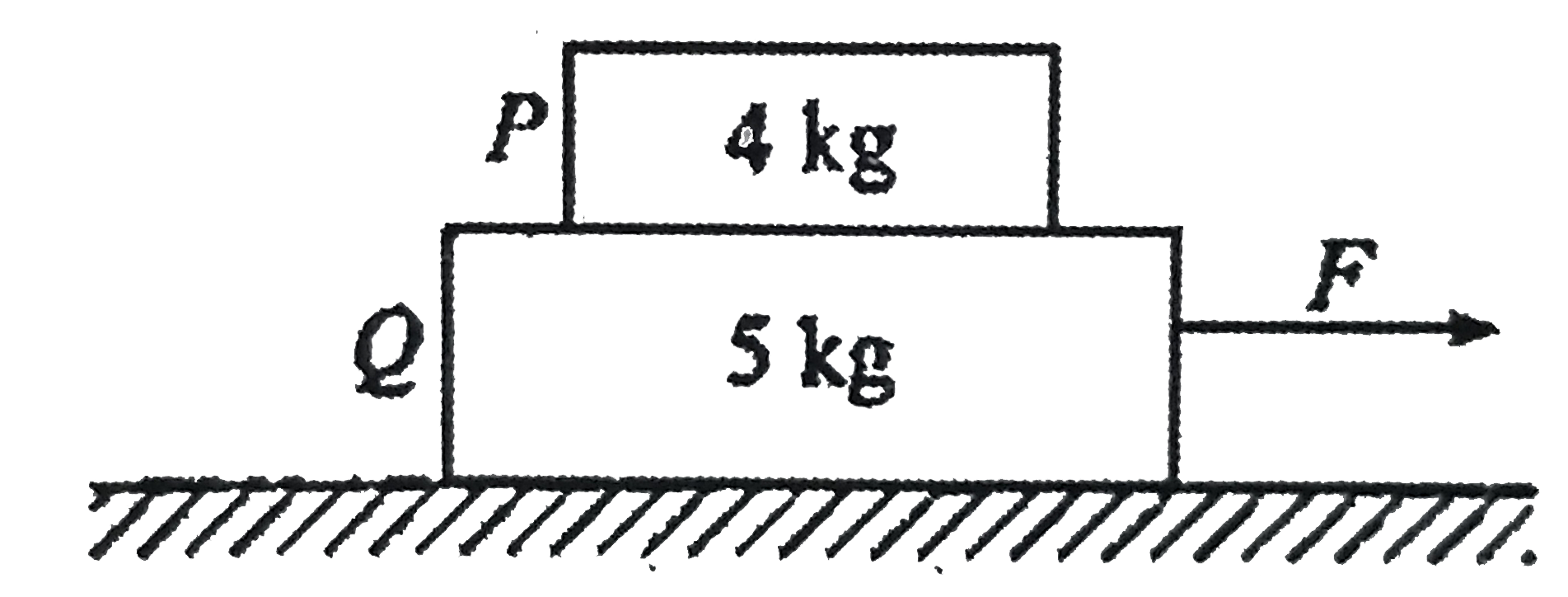
View SolutionThe coefficient of friction between 4 kg and 5 kg blocks is 0.2 and between 5 kg block and ground is 0.1 respectively. Choose the correct statement : (Take g=10m/s2)
View Solution