A 4.0 kg mess kit sliding on a frictionless surface explodes into two 2.0 kg parts: 3.0 m/s, due north, and 6.0 m/s, 30∘ north of east. What is the original speed of the mess kit ?
The correct Answer is:3.9 m/s
To solve the problem of finding the original speed of the mess kit after it explodes into two parts, we will use the principle of conservation of momentum. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Problem
The mess kit has a mass of 4.0 kg and is moving on a frictionless surface. It explodes into two parts, each with a mass of 2.0 kg. One part moves at 3.0 m/s due north, and the other moves at 6.0 m/s at an angle of 30° north of east. We need to find the original speed of the mess kit before the explosion.
Step 2: Set Up the Momentum Conservation Equation
According to the conservation of momentum, the total momentum before the explosion (initial momentum) must equal the total momentum after the explosion (final momentum).
Let →Pinitial be the initial momentum of the mess kit and →Pfinal be the total final momentum of the two parts.
→Pinitial=→Pfinal
Step 3: Calculate the Final Momentum of Each Part
1. Momentum of the first part (2.0 kg, 3.0 m/s due north):
- Mass m1=2.0kg
- Velocity →v1=3.0m/s^j
- Momentum →P1=m1→v1=2.0×3.0^j=6.0^jkg m/s
2. Momentum of the second part (2.0 kg, 6.0 m/s at 30° north of east):
- Mass m2=2.0kg
- Velocity components:
- v2x=6.0cos(30°)=6.0×√32=3√3m/s
- v2y=6.0sin(30°)=6.0×12=3.0m/s
- Momentum →P2=m2→v2=2.0×(3√3^i+3.0^j)=6√3^i+6.0^jkg m/s
Step 4: Calculate Total Final Momentum
Now, we can find the total final momentum →Pfinal by adding →P1 and →P2:
→Pfinal=→P1+→P2=(6√3^i+6.0^j)+(0^i+6.0^j)=6√3^i+12.0^jkg m/s
Step 5: Calculate the Initial Momentum
The initial momentum of the mess kit can be expressed as:
→Pinitial=mtotal⋅→vinitial=4.0kg⋅→vinitial
Step 6: Set Initial Momentum Equal to Final Momentum
Since momentum is conserved:
4.0⋅→vinitial=6√3^i+12.0^j
Step 7: Solve for →vinitial
To find →vinitial:
→vinitial=6√34.0^i+12.04.0^j=3√32^i+3.0^j
Step 8: Calculate the Magnitude of →vinitial
The magnitude of the initial velocity is:
|→vinitial|=
⎷(3√32)2+(3.0)2
Calculating:
|→vinitial|=√274+9=√274+364=√634=√632≈3.96m/s
Conclusion
The original speed of the mess kit before the explosion is approximately 3.96 m/s.
---
The mess kit has a mass of 4.0 kg and is moving on a frictionless surface. It explodes into two parts, each with a mass of 2.0 kg. One part moves at 3.0 m/s due north, and the other moves at 6.0 m/s at an angle of 30° north of east. We need to find the original speed of the mess kit before the explosion.
According to the conservation of momentum, the total momentum before the explosion (initial momentum) must equal the total momentum after the explosion (final momentum).
1. Momentum of the first part (2.0 kg, 3.0 m/s due north):
- Mass m1=2.0kg
- Velocity →v1=3.0m/s^j
- Momentum →P1=m1→v1=2.0×3.0^j=6.0^jkg m/s
- Mass m2=2.0kg
- Velocity components:
- v2x=6.0cos(30°)=6.0×√32=3√3m/s
- v2y=6.0sin(30°)=6.0×12=3.0m/s
- Momentum →P2=m2→v2=2.0×(3√3^i+3.0^j)=6√3^i+6.0^jkg m/s
Now, we can find the total final momentum →Pfinal by adding →P1 and →P2:
The initial momentum of the mess kit can be expressed as:
Since momentum is conserved:
To find →vinitial:
The magnitude of the initial velocity is:
⎷(3√32)2+(3.0)2
The original speed of the mess kit before the explosion is approximately 3.96 m/s.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Single Correct Choice )47videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (More than One Correct Choice)5videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )4videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTION (INTEGER TYPE)3videos
CAPACITANCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)3videos
CIRCUITS
Similar Questions
A 2.0-kg pistol fires a 1.0-g bullet with a muzzle speed of 1000 m/s. The bullet then strikes a 10-kg wooden block resting on a horizontal frictionless surface. The block and the embedded bullet then slide across the surface.

What is the speed of the "bullet + block" system immediately after the bullet is embedded in the block?View SolutionA 2.0-kg pistol fires a 1.0-g bullet with a muzzle speed of 1000 m/s. The bullet then strikes a 10-kg wooden block resting on a horizontal frictionless surface. The block and the embedded bullet then slide across the surface.

What is the kinetic energy of the bullet as it travels toward the block?View Solution
Knowledge Check
- Question 1 - Select One
Two forces are applied to a 5.0 kg crate, one is 6.0N to the north and the other is 8.0N to the west. The magnitude of the acceleration of the crate is :
A0.50m/s2B2.0m/s2C2.8m/s2D10m/s2 - Question 2 - Select One
A block of mass 4kg slides on a horizontal frictionless surface with a speed of 2m/s. It is brought to rest in compressing a spring in its path. If the force constant of the spring is 400N/m, by how much the spring will be compressed
A2×10−2mB0.2mC20mD200m - Question 3 - Select One
A truck travelling due north at 20 m/s turns east and travels at the same speed. What is the change in velocity :
A40 m/s north eastB20√2 m/s south eastC20√2 m/s south westD20√2 m/s north west
A 30 kg Sell is flying at 36m/s. When the shell explodes into two parts of 12kg and 18kg , the lighter part stops, and heavier part files on . What is the velocity of heavier part ? .
View SolutionA 4.0-kg block slides along a frictionless surface with a constant speed of 5.0 m/s as shown. Two seconds after it begins sliding, a horizontal, time-dependent force is applied to the mass. The force is removed 8 s later. The graph shows how the force on the block varies with time.
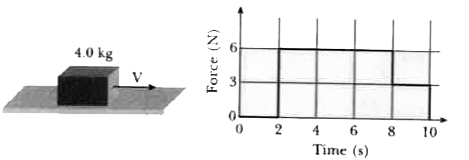
What is the approximate speed of the block at t =11 s?View SolutionTwo beetles run across flat send, starting at the same point. Beetle 1 runs 0.50 m due east, the 0.80 m at 30∘ north of due east. Beetle 2 also makes two runs, the first is 1.6m at 40∘ east of due north. What must be (a) the magnitude and (b) the direction of its second run if it is to end up at the new location of beetle 1 ?
View SolutionA person moves 30 m north. Then 30 m east, then 30√2 m south-west. His displacement from the original position is
View SolutionA 35-kg girl is standing near and to the left of a 43-kg boy on the frictionless surface of a frozen pond. The boy throws a 0.75-kg ice ball to the girl with a horizontal speed of 6.2 m/s. What are the velocities of the boy and the girl immediately after the girl catches the ice ball?
View Solution

