A 15.0 kg package is moving at a speed of 10.0 m/s vertically upward along a y axis when it explodes into three fragments: a 2.00 kg fragment is shot upward with an initial speed of 20.0 m/s and a 3.00 kg fragment is shot in the positive direction of a horizontal x axis with an initial speed of 5.00 m/s. Find (a) the speed of the third fragment right after the explosion and (b) the total kinetic energy provided by the explosion.
The correct Answer is:(a)11.1 m/s ; (b) 304 J
To solve the problem, we will break it down into two parts: (a) finding the speed of the third fragment after the explosion and (b) calculating the total kinetic energy provided by the explosion.
Part (a): Finding the Speed of the Third Fragment
1. Initial Momentum Calculation:
- The initial momentum of the system (the package) before the explosion can be calculated using the formula:
pinitial=minitial⋅vinitial=15kg⋅10m/s=150kg m/s^j
- This momentum is directed vertically upward along the y-axis.
2. Final Momentum Calculation:
- After the explosion, the package breaks into three fragments:
- Fragment 1: m1=2kg, v1=20m/s (upward)
- Fragment 2: m2=3kg, v2=5m/s (horizontal, x-direction)
- Fragment 3: m3=10kg (unknown speed v3)
3. Conservation of Momentum:
- According to the law of conservation of momentum, the total momentum before the explosion equals the total momentum after the explosion:
pinitial=pfinal
- The final momentum can be expressed as:
pfinal=m1v1^j+m2v2^i+m3v3
- Substituting the values:
150^j=(2⋅20)^j+(3⋅5)^i+(10⋅v3)
- This simplifies to:
150^j=40^j+15^i+10v3
4. Separating Components:
- For the y-component:
150=40+10v3y⟹10v3y=110⟹v3y=11m/s
- For the x-component:
0=15+10v3x⟹10v3x=−15⟹v3x=−1.5m/s
5. Magnitude of the Velocity of the Third Fragment:
- The speed of the third fragment v3 can be calculated using the Pythagorean theorem:
v3=√v23x+v23y=√(−1.5)2+(11)2=√2.25+121=√123.25≈11.1m/s
Part (b): Total Kinetic Energy Provided by the Explosion
1. Initial Kinetic Energy:
- The initial kinetic energy KEinitial of the package is given by:
KEinitial=12minitialv2initial=12⋅15⋅(10)2=12⋅15⋅100=750J
2. Final Kinetic Energy:
- The final kinetic energy KEfinal of the fragments is:
KEfinal=12m1v21+12m2v22+12m3v23
- Substituting the values:
KEfinal=12⋅2⋅(20)2+12⋅3⋅(5)2+12⋅10⋅(11.1)2
- Calculating each term:
- For fragment 1: 12⋅2⋅400=400J
- For fragment 2: 12⋅3⋅25=37.5J
- For fragment 3: 12⋅10⋅123.21≈616.05J
- Thus:
KEfinal=400+37.5+616.05≈1053.55J
3. Total Kinetic Energy Provided by the Explosion:
- The change in kinetic energy ΔKE is:
ΔKE=KEfinal−KEinitial=1053.55−750=303.55J
Final Answers:
- (a) The speed of the third fragment is approximately 11.1 m/s.
- (b) The total kinetic energy provided by the explosion is approximately 303.55 J.
- The initial momentum of the system (the package) before the explosion can be calculated using the formula:
pinitial=minitial⋅vinitial=15kg⋅10m/s=150kg m/s^j
- This momentum is directed vertically upward along the y-axis.
- After the explosion, the package breaks into three fragments:
- Fragment 1: m1=2kg, v1=20m/s (upward)
- Fragment 2: m2=3kg, v2=5m/s (horizontal, x-direction)
- Fragment 3: m3=10kg (unknown speed v3)
- According to the law of conservation of momentum, the total momentum before the explosion equals the total momentum after the explosion:
pinitial=pfinal
- The final momentum can be expressed as:
pfinal=m1v1^j+m2v2^i+m3v3
- Substituting the values:
150^j=(2⋅20)^j+(3⋅5)^i+(10⋅v3)
- This simplifies to:
150^j=40^j+15^i+10v3
- For the y-component:
150=40+10v3y⟹10v3y=110⟹v3y=11m/s
- For the x-component:
0=15+10v3x⟹10v3x=−15⟹v3x=−1.5m/s
- The speed of the third fragment v3 can be calculated using the Pythagorean theorem:
v3=√v23x+v23y=√(−1.5)2+(11)2=√2.25+121=√123.25≈11.1m/s
- The initial kinetic energy KEinitial of the package is given by:
KEinitial=12minitialv2initial=12⋅15⋅(10)2=12⋅15⋅100=750J
- The final kinetic energy KEfinal of the fragments is:
KEfinal=12m1v21+12m2v22+12m3v23
- Substituting the values:
KEfinal=12⋅2⋅(20)2+12⋅3⋅(5)2+12⋅10⋅(11.1)2
- Calculating each term:
- For fragment 1: 12⋅2⋅400=400J
- For fragment 2: 12⋅3⋅25=37.5J
- For fragment 3: 12⋅10⋅123.21≈616.05J
- Thus:
KEfinal=400+37.5+616.05≈1053.55J
- The change in kinetic energy ΔKE is:
ΔKE=KEfinal−KEinitial=1053.55−750=303.55J
- (a) The speed of the third fragment is approximately 11.1 m/s.
- (b) The total kinetic energy provided by the explosion is approximately 303.55 J.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Single Correct Choice )47videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (More than One Correct Choice)5videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )4videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTION (INTEGER TYPE)3videos
CAPACITANCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)3videos
CIRCUITS
Similar Questions
A shell is fixed from a cannon with a speed of 100m/s at an angle 60∘ with the horizontal (positive x-direction). At the highest point of its trajectory, the shell explodes into two equal fragments. One of the fragments moves along the negative x-direction with a speed of 50m/s. What is the speed of the other fragment at the time of explosion.
View SolutionA shell is fired from a cannon with a speed of 100m/s at an angle 30∘with the vertical (y-direction). At the highest point of its trajectory, the shell explodes into two fragments of masses in the ratio 1:2. The lighter fragment moves vertically upwards with an initial speed of 200m/s. What is the speed of the heavier fragment at the time of explosion?
View Solution
Knowledge Check
- Question 1 - Select One
The KE and PE of the ball half way up, when a ball of mass 0.1 kg is thrown vertically upwards with an initial speed of 20 m/s is
A10 J, 20 JB15 J, 8JC8 J, 16 JD10 J, 10 J - Question 2 - Select One
A stone of 3 kg is thrown vertically upward with an initial speed of 20 m/s. If g=10m/s2, then find the kinetic energy and potential energy after 1 s.
A600, 1800B600,0C100, 500D150, 450 - Question 3 - Select One
A stone of 3kg is thrown vertically upward with an initial speed of 20m/s. If g=10m/s2, then find the kinetic energy and potential energy after 1s.
A600, 1800B600,0C100, 500D150, 450
A shell is fired from a cannon with a speed of 100m/s at an angle 60∘ with the horizontal (positive x-direction). At the highest point of its trajectory, the shell explodes in to two equal fragments. One of the fragments moves is the speed of the other fragment at the time of explosion.
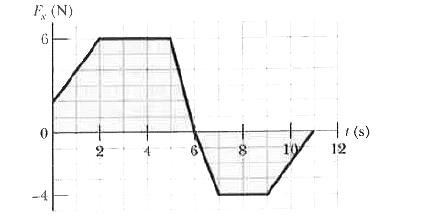
View SolutionFigure 5-58 gives, as a function of time l, the force component F, that acts on a 3.00 kg ice block is moving in the positive direction of the axis, with a speed of 3.0 m/s. What are its speed and (b) direction of travel of travel at t = 11 s ?
 View Solution
View SolutionHow much power is needed to lift a 75- kg student vertically upward at a constant speed of 0.33 m/s ?
View SolutionA bom of mass 1kg is thrown vertically upwards with a speed of 100m/s. After 5 seconds, it explodes into two fragments. One fragment of mass 400gm is found to go down with a speed of 25m/s. What will happen to the second fragment just after the explosion ? (g=10ms−1)
View SolutionA projectile of mass 30 kg is shot vertically upwards with an intial velocity of 10 m/s.After 5 s, it explodes into two fragments, one of which having a mass of 20 kg is travelling vertically with a velocity of 150m/s. What is the velocity of the other fragment at that instant?
View Solution

