A 40 N block is supported by two ropes. One rope is horizontal and other makes an angle of with the ceiling. The tension in the rope attached to the ceiling is approximately
80 N
40 N
34.6 N
46.2 N
The correct Answer is:A
To solve the problem of finding the tension in the rope attached to the ceiling, we can follow these steps:
Step 1: Identify the Forces Acting on the Block
The block has a weight acting downward, which is given as 40 N. There are two tension forces acting on the block:
1. The tension T1 in the horizontal rope.
2. The tension T2 in the rope that makes an angle of 30° with the ceiling.
Step 2: Resolve the Tension in the Rope at an Angle
The tension T2 can be resolved into two components:
- A vertical component T2y=T2sin(30°)
- A horizontal component T2x=T2cos(30°)
Step 3: Apply the Equilibrium Condition in the Vertical Direction
Since the block is in equilibrium, the sum of the vertical forces must equal zero. Therefore, we can write the equation:
T2y+T1=40N
Substituting the vertical component:
T2sin(30°)+T1=40
Step 4: Calculate the Value of sin(30°)
From trigonometric values, we know:
sin(30°)=12
Thus, we can rewrite the equation:
T2⋅12+T1=40
Step 5: Apply the Equilibrium Condition in the Horizontal Direction
In the horizontal direction, the only force acting is the horizontal component of the tension T2:
T2x=T1
Substituting the horizontal component:
T2cos(30°)=T1
Step 6: Calculate the Value of cos(30°)
From trigonometric values, we know:
cos(30°)=√32
Thus, we can rewrite the equation:
T2⋅√32=T1
Step 7: Substitute T1 into the Vertical Force Equation
Now we can substitute T1 from the horizontal equation into the vertical equation:
T2⋅12+T2⋅√32=40
Step 8: Factor Out T2
Factoring out T2:
T2(12+√32)=40
Step 9: Simplify the Equation
Combining the terms inside the parentheses:
T2(1+√32)=40
Step 10: Solve for T2
Now, we can solve for T2:
T2=40⋅21+√3
Step 11: Calculate the Numerical Value
Calculating the value:
1. 1+√3≈1+1.732=2.732
2. T2≈802.732≈29.3N
Thus, the tension in the rope attached to the ceiling T2 is approximately 29.3 N.
The block has a weight acting downward, which is given as 40 N. There are two tension forces acting on the block:
1. The tension T1 in the horizontal rope.
2. The tension T2 in the rope that makes an angle of 30° with the ceiling.
The tension T2 can be resolved into two components:
- A vertical component T2y=T2sin(30°)
- A horizontal component T2x=T2cos(30°)
Since the block is in equilibrium, the sum of the vertical forces must equal zero. Therefore, we can write the equation:
T2y+T1=40N
Substituting the vertical component:
T2sin(30°)+T1=40
From trigonometric values, we know:
sin(30°)=12
Thus, we can rewrite the equation:
T2⋅12+T1=40
In the horizontal direction, the only force acting is the horizontal component of the tension T2:
T2x=T1
Substituting the horizontal component:
T2cos(30°)=T1
From trigonometric values, we know:
cos(30°)=√32
Thus, we can rewrite the equation:
T2⋅√32=T1
Now we can substitute T1 from the horizontal equation into the vertical equation:
T2⋅12+T2⋅√32=40
Factoring out T2:
T2(12+√32)=40
Combining the terms inside the parentheses:
T2(1+√32)=40
Now, we can solve for T2:
T2=40⋅21+√3
Calculating the value:
1. 1+√3≈1+1.732=2.732
2. T2≈802.732≈29.3N
Topper's Solved these Questions
- NEWTONS LAWS OF MOTION AND FRICTIONBOOK - BITSAT GUIDECHAPTER - NEWTONS LAWS OF MOTION AND FRICTIONEXERCISE - BITSAT Archives
23 Videos
- MOTION IN !,2,2 DIMENSIONS AND POJECTILE MOTIONBOOK - BITSAT GUIDECHAPTER - MOTION IN !,2,2 DIMENSIONS AND POJECTILE MOTIONEXERCISE - All Questions
86 Videos
- ROTATIONAL MOTIONBOOK - BITSAT GUIDECHAPTER - ROTATIONAL MOTIONEXERCISE - BITSAT Archives
9 Videos
Similar Questions
A block weighing 4N is supported by two ropes Once rope is horizontal and the other makes an angle of 30∘ with the ceilling The tension (in newton) in the rope attached to the ceilling is .
View SolutionA sphere of radius R is supported by a rope attached to the wall. The rope makes an angle θ=45∘ with respect to the wall. The point where the rope is attached to the wall is at a distance of 3R2 from the point where the sphere touches the wall. Find the minimum coefficient of friction (μ) between the wall and the sphere for this equilibrium to be possible.
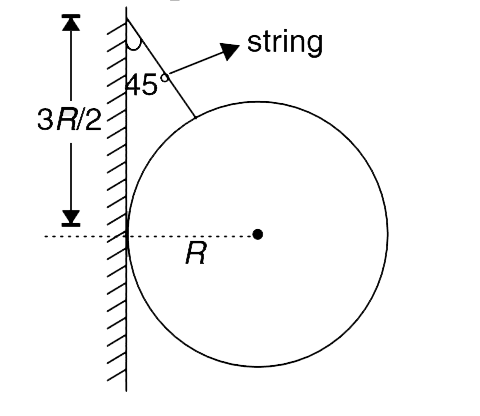
View Solution
Knowledge Check
A 40 N block is supported by two ropes. One rope is horizontal and the other makes an angle of 30∘ with the ceiling. The tension in the rope attached to the ceiling is approximately :
A80 NB40 NC34.6 ND46.2 NA rope of mass 0.2 kg is connected at the same height of two opposite walls. It is allowed to hang under its own weight. At the contact point between the rope and the wall, the rope makes an angle θ=30%∘ with respect to horizontal. The tension in the rope at its midpoint between the walls is
A1.78 NB1.56 NC1.82 ND1.96 NAn object of mass 5 kg is attached to the end ofa rope. If the rope is pulled upward with an acceleration 0.30ms−2, what is the tension in the rope?
A30.5 NB40.5 NC50.5 ND60.5 N
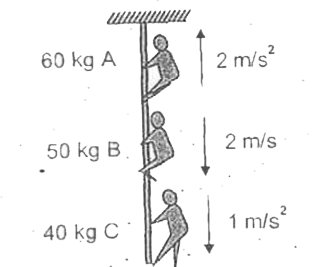
Tension in the rope at the rigid support is (g=10m/s2)
View SolutionA mass of 3kg is suspended by a rope of length 2m from the ceiling. A force of 40 N in the horizonal direction is applied at midpoint P of the rope as shown. What is the angle the rope makes with the vertical in equilibrium and the tension in part of string attached to the ceiling? (Neglect the mass of the rope, g=10m/s2)
View SolutionA mass of 3kg is suspended by a rope of length 2m from the ceilling A force of 40N in the horizontal direction is applied atmidpoint P of the rope the as shown. What is the angle the rope makes with the vertical in equilibrium and the tension in part of string attached to the ceiling ? (Neglect the mass of the rope, g=10m/s2) .
View SolutionA straight rope of length 'L' is kept on a frictionless horizontal surface and a force 'F' is applied to one end of the rope in the direction of its length and away from that end. The tension in the rope at a distance 'I from that end is 9
View SolutionA uniform rope of mass m and length L is attached to the ceiling of a lift. The other end of the rope is attached to a block of mass M. The lift is moving up with a constant acceleration a0. Find the tension in the rope at a distance x from the ceiling as shown in the diagram.

View Solution
