A 50g mass hangs at the end of a massless spring. When 20g more are added to the end of the spring, it stretches 7.0cm more. (a) Find the spring constant. (b) If the 20g are now removed, what will be the period of the motion ?
The correct Answer is:A, B, D
(a) kx=mg
∴k=mgx=(20×10−3)(10)7×10−2
=207N/m
(b) T=2π√mk
=2π√50×10−320/7 = 0.84 s
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Single Correct
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 More Than One Correct
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Single Correct
24 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A 0.2kg of mass hangs at the end of a spring. When 0.002kg more mass is added to the end of the spring, it stretches 7 cm more. If the 0.02 kg mass is removed what will be the period of vibration of the system?
View SolutionA mass of 0.1 kg hangs at the end of a spring. When a mass of 0.01 kg more is added at the end of the spring, it stretches by 5 cm more. When the extra 0.01 kg mass is removed, determine the time period of vibration of the system.
View Solution
Knowledge Check
Three masses of 500g, 300g and 100g are suspended at the end of a spring as shown and are in equilibrium. When the 500g mass is removed suddenly, the system oscillates with a period of 2s. When the 300g mass is also removed, it will oscillate with period T. Find the value of T.
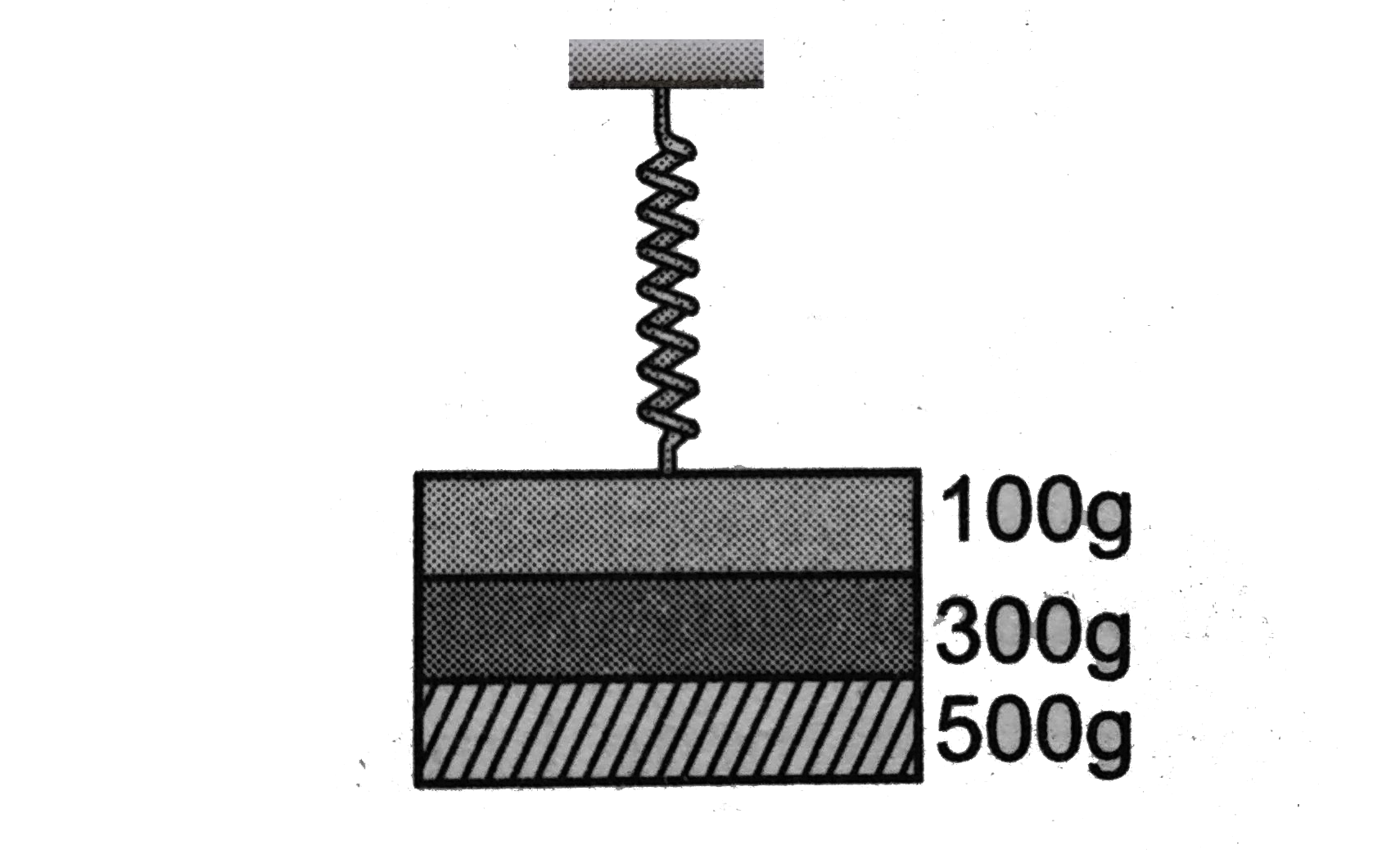 A1 sB2 sC3 sD4 s
A1 sB2 sC3 sD4 sThree masses 700g, 500g, and 400 g are suspended at the end of a spring a shown and are in equilibrium. When the 700 g mass is removed, the system oscillacts with a period of 3 seconds, when the 500 gm mass is also removed, it will oscillate with a period of
 A1 sB2 sC3 sD√125s
A1 sB2 sC3 sD√125sWhen a 20 g mass hangs attached to one end of a light spring of length 10 cm, the spring stretches by 2 cm. The mass is pulled down until the total length of the spring is 14 cm. The elastic energy, (in Joule) stored in the spring is :
A4×10−2B4×10−3C8×10−2D8×10−3
By what fraction does the mass of a spring is 200 g at its natural lenth and the spring constant is 500 N m ^(-1)
View SolutionWhen a 1.0kg mass hangs attached to a spring of length 50cm, the spring stretches by 2cm. The mass is pulled down until the length of the spring becomes 60cm. What is the amount of elastic energy stored in the spring in this condition. if g=10m/s2.
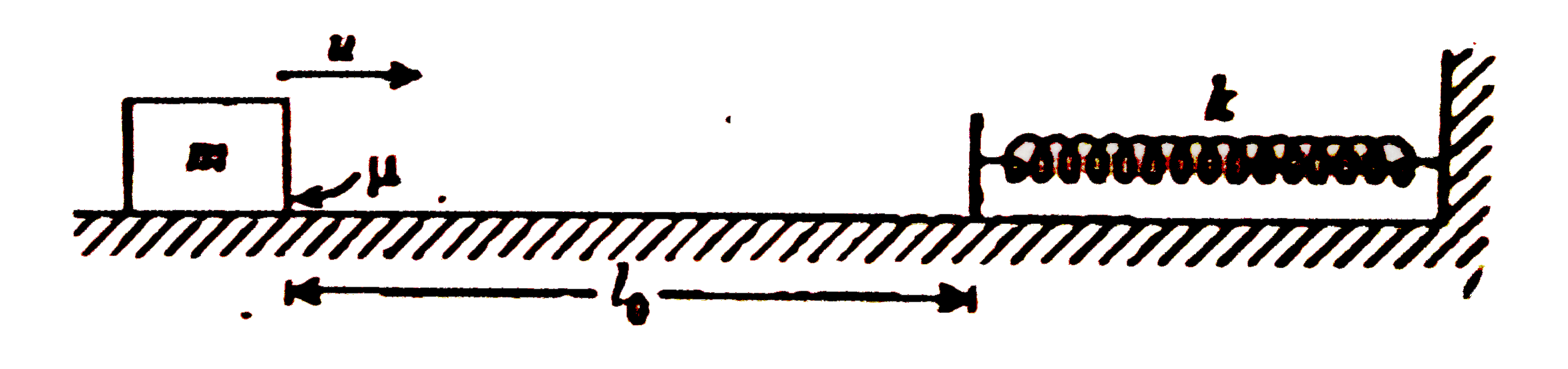
View SolutionFigure. shows a rough horizontal plane which ends in a vertical wall, to which a spring is connected, having a force constant k. Initially spring is in its relaxed state. A block of mass m starts with an initial velocity u towards the spring from a distance l0 from the end of spring shown. When block strikes at the end ofthe spring, it compresses the spring and comes to rest. Find the maximum compression in the spring. The friction coefficient between the block and the floor is μ..
View Solutionspring of force constant k clamped rigidly at onoe end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in figure is stretched by the same force F.
(a) What is the maximum extension of the spring in the two cases ?
(b) If the mass in figure and the two masses in figure are released free, what is the period of oscillation in each case?

View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View Solution
