A 9.0 kg box of oranges slides from rest down a frictionless incline from a height of 5.0 m. A constant frictional force, introduced at point A, brings the block to rest at point B, 19 m to the right of point A.

What is the coefficient of kinetic friction, μk, of the surface from A to B ?
0.11
0.33
0.26
0.47
The correct Answer is:C
Step by step video & image solution for A 9.0 kg box of oranges slides from rest down a frictionless incline from a height of 5.0 m. A constant frictional force, introduced at point A, brings the block to rest at point B, 19 m to the right of point A. What is the coefficient of kinetic friction, mu_(k), of the surface from A to B ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, POWER, AND ENERGYBook:RESNICK AND HALLIDAYChapter:WORK, POWER, AND ENERGYExercise:PRACTICE QUESTIONS (Matrix-Match)
Explore 1 Video
- WORK, POWER, AND ENERGYBook:RESNICK AND HALLIDAYChapter:WORK, POWER, AND ENERGYExercise:PRACTICE QUESTIONS (Integer Type)
Explore 5 Videos
- WORK, POWER, AND ENERGYBook:RESNICK AND HALLIDAYChapter:WORK, POWER, AND ENERGYExercise:PRACTICE QUESTIONS (More than one choice correct type)
Explore 10 Videos
- WAVES-IBook:RESNICK AND HALLIDAYChapter:WAVES-IExercise:Practice Questions (Integer Type)
Explore 4 Videos
Similar Questions
In Fig. , block 1 of mass m1 slides from rest along a frictionless ramp from height h = 3.00 m and then collides with stationary block 2, which has mass m2=2.00m1. After the collision, block 2 slides into a region where the coefficient of kinetic friction μk is 0.450 and comes to a stop in distance d within that region. What is the value of distance d if the collision is (a) elastic and (b) completely inelastic?

View SolutionA block is released at A and slides on smooth surface in shape of quarter circel. The horizontal part is rough if the block comes to rest 1.0 m away from B, then what is the coefficient of kinetic friction?
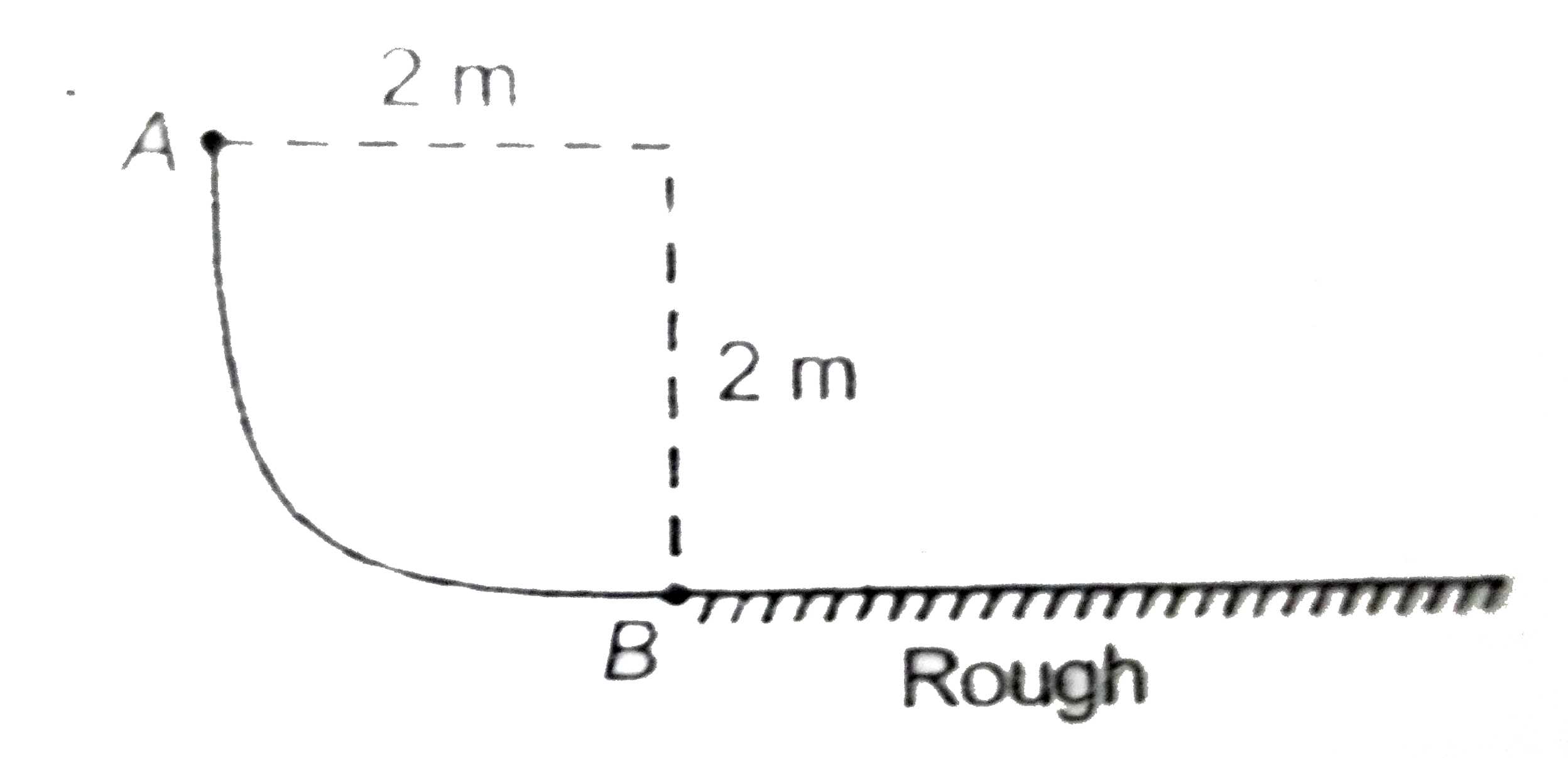
View Solution
Knowledge Check
A ring of mass m sliding on a smooth surface with velocity v0 enters rough surface with coefficient of kinetic friction μk, then
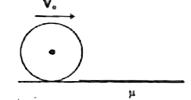 Athe linear distance moved by centre of mass before the ring starts pure rolling is 3v208μkgBthe gain in kinetic energy is mv208Cthe loss in kinetic energy is mv204Dthe work done by friction force is −3mv208
Athe linear distance moved by centre of mass before the ring starts pure rolling is 3v208μkgBthe gain in kinetic energy is mv208Cthe loss in kinetic energy is mv204Dthe work done by friction force is −3mv208A block is released from rest from point on a rough inclined place of inclination 37∘. The coefficient of friction is 0.5.
AThe time taken to slide down 9 m on the plane is 3 s.BThe velocity of block after moving 4 m is m/s.CThe block travels equal distances in equal intervals of time.DThe velocity of block increases linearly.A block of mass M is sliding down the plane. Coefficient of static friction is μs and kinetic friction is μk. Then friction force acting on the block is :
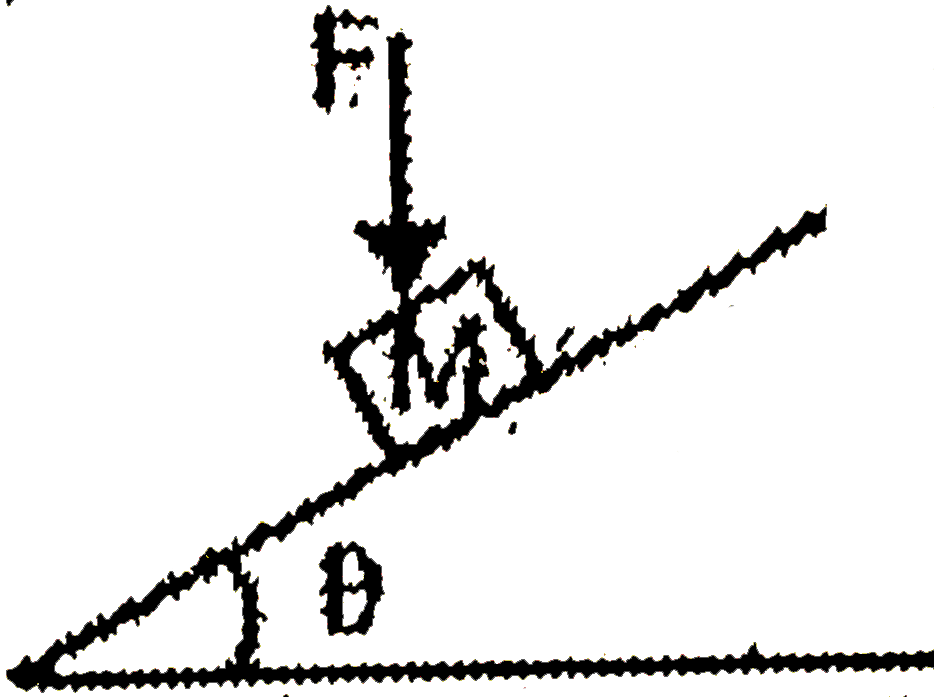 A(F+Mg)sinθBμk(F+Mg)cosθCμsMgcosθD(Mg+F)sinθ
A(F+Mg)sinθBμk(F+Mg)cosθCμsMgcosθD(Mg+F)sinθ
A block slides down as incline of 60∘ with the horizontal. Starting from rest, it covers 8 m in the first 2 seconds. Find the coefficient of static friction
View SolutionA block A of weight W slide down an inclined plane S of slope 37∘at a constant velocity, while the plank B also of weight W rests on top of A. The plank B is attached by a cord to the top of plane .The coefficient of kinetic friction μ is the same between the surface A and B and between S and A Determine the value of 1/μ
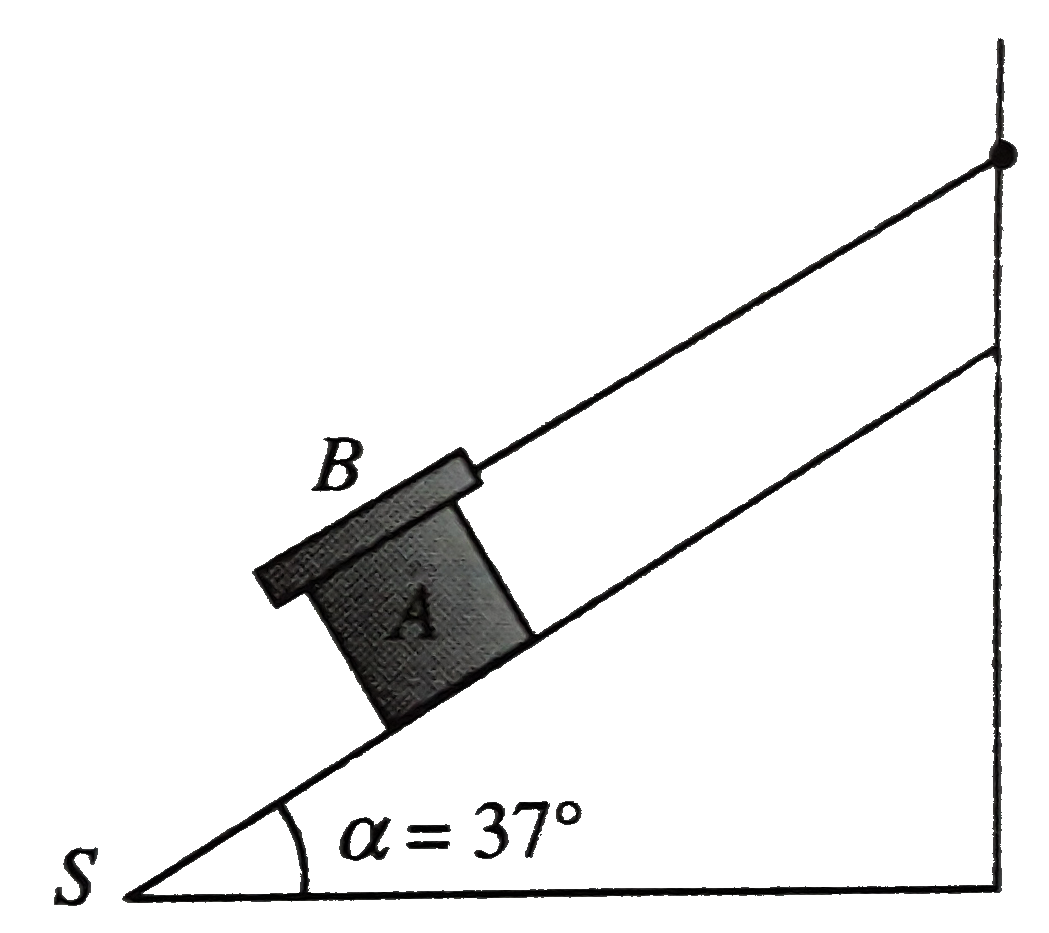
View SolutionBlock of mass m are released from rest and they slide down the inclined surface as shown in figure. Show that the work done by the frictional forces on the blocks are same in all the cases. Also calculate the speeds with which the blocks reach point B. The coefficient of friction for all the surface is μk.

View SolutionA block slides down an inclined surface of inclination 300 with the horizontal. Starting from rest it covers 8 m in the first two seconds. Find the coefficietn of kinetic friction between the two.
View SolutionA block slides down an incline of 30∘ with the horizontal starting from rest it covers 8m in the first two seconds Find the coefficient of kinetic friction between the two .
View Solution