'A' and 'B' are the two pegs separated by 13 cm. A body of 169 Kgwt is suspended by thread of 17 cm connecting to A & B, such that the two segments of strings are perpendicular. Then tensions in shorter and longer parts of string having are
100 kgwt, 69 kgwt
65 kgwt, 156. kgwt
156 kgwt, 65 kgwt
69 kgwt, 100 kgwt
The correct Answer is:C
To solve the problem, we need to find the tensions in the shorter and longer parts of the string connecting pegs A and B. Let's break this down step-by-step.
Step 1: Understand the Geometry
We have two pegs A and B that are 13 cm apart. A body weighing 169 kg is suspended by a string of total length 17 cm, with the segments of the string being perpendicular to each other.
Step 2: Define Variables
Let:
- T1 = tension in the shorter part of the string
- T2 = tension in the longer part of the string
- X = length of the shorter segment of the string
- 17−X = length of the longer segment of the string
Step 3: Apply Pythagorean Theorem
Since the segments of the string are perpendicular, we can apply the Pythagorean theorem:
X2+(17−X)2=132
Expanding this:
X2+(289−34X+X2)=169
Combining like terms:
2X2−34X+120=0
Step 4: Solve the Quadratic Equation
Using the quadratic formula X=−b±√b2−4ac2a:
- Here, a=2, b=−34, and c=120.
X=34±√(−34)2−4⋅2⋅1202⋅2
Calculating the discriminant:
342−960=1156−960=196
So,
X=34±144
Calculating the two possible values:
X1=484=12andX2=204=5
Step 5: Determine Cosine Values
Now, we can find cosθ1 and cosθ2:
- For X=5: cosθ1=513 and cosθ2=1213
- For X=12: cosθ1=1213 and cosθ2=513
Step 6: Set Up the Tension Equations
From the equilibrium of forces in the horizontal direction:
T1cosθ1=T2cosθ2
Substituting the cosine values:
T1⋅513=T2⋅1213
Cancelling 1313:
T1=125T2(Equation 1)
Step 7: Set Up the Vertical Force Balance
From the equilibrium of forces in the vertical direction:
T1sinθ1+T2sinθ2=169
Substituting the sine values:
T1⋅1213+T2⋅513=169
Multiplying through by 13:
12T1+5T2=169⋅13(Equation 2)
Step 8: Substitute Equation 1 into Equation 2
Substituting T1=125T2 into Equation 2:
12(125T2)+5T2=169⋅13
This simplifies to:
1445T2+5T2=169⋅13
Converting 5T2 to a fraction:
1445T2+255T2=169⋅13
Combining terms:
1695T2=169⋅13
Cancelling 169:
T2=13⋅5=65 kg
Step 9: Find T1
Now substituting T2 back into Equation 1:
T1=125⋅65=156 kg
Final Result
Thus, the tensions in the shorter and longer parts of the string are:
- T1=156 kg
- T2=65 kg
We have two pegs A and B that are 13 cm apart. A body weighing 169 kg is suspended by a string of total length 17 cm, with the segments of the string being perpendicular to each other.
Let:
- T1 = tension in the shorter part of the string
- T2 = tension in the longer part of the string
- X = length of the shorter segment of the string
- 17−X = length of the longer segment of the string
Since the segments of the string are perpendicular, we can apply the Pythagorean theorem:
X2+(17−X)2=132
Expanding this:
X2+(289−34X+X2)=169
Combining like terms:
2X2−34X+120=0
Using the quadratic formula X=−b±√b2−4ac2a:
- Here, a=2, b=−34, and c=120.
X=34±√(−34)2−4⋅2⋅1202⋅2
Calculating the discriminant:
342−960=1156−960=196
So,
X=34±144
Calculating the two possible values:
X1=484=12andX2=204=5
Now, we can find cosθ1 and cosθ2:
- For X=5: cosθ1=513 and cosθ2=1213
- For X=12: cosθ1=1213 and cosθ2=513
From the equilibrium of forces in the horizontal direction:
T1cosθ1=T2cosθ2
Substituting the cosine values:
T1⋅513=T2⋅1213
Cancelling 1313:
T1=125T2(Equation 1)
From the equilibrium of forces in the vertical direction:
T1sinθ1+T2sinθ2=169
Substituting the sine values:
T1⋅1213+T2⋅513=169
Multiplying through by 13:
12T1+5T2=169⋅13(Equation 2)
Substituting T1=125T2 into Equation 2:
12(125T2)+5T2=169⋅13
This simplifies to:
1445T2+5T2=169⋅13
Converting 5T2 to a fraction:
1445T2+255T2=169⋅13
Combining terms:
1695T2=169⋅13
Cancelling 169:
T2=13⋅5=65 kg
Now substituting T2 back into Equation 1:
T1=125⋅65=156 kg
Thus, the tensions in the shorter and longer parts of the string are:
- T1=156 kg
- T2=65 kg
Similar Questions
Two particles of masses m1andm2 are connected to a string and the system is rotated in a horizontal plane with 'P' as center. The ratio of tension in the two parts of string is

View SolutionA body of mass m is suspended by two strings making angles αandβ with the horizontal. Find the tensions in the strings.
View SolutionA cylinder of mass m is suspended through two strings wrapped around it as shwon in figure . Find a. the tension T in the string and b. the speed o the cylinder as it falls through a distance h.

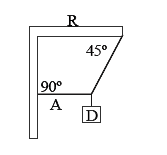
View SolutionA blolck D weighing 300kg is suspended by means of two cords A and B as shown in the figure. W is a vertical wall and R a horizontal rigid beam. The tension in the string A in kg is :
View SolutionA body of mass 50 kg, suspended by two strings of lengths 30 cm and 40 cm fastend to two points in the same horizontal line 50 cm apart, is in equilibrium. Find the tension (in Newtons) in each string.
View SolutionTwo indentical balls, each having a charge of 2.00×10−7C and a mass of 100g , are suspended from a common point by two insulating strings each 50 cm long. The balls are held at a separation 5.0cm apart and then released. Find (a) the electric force on one of the charged balls (b) the components of the resultant force on it along and perpendicular to the string (c) the tension is the string (d) the acceleration of one of the balls. Answers are to be obtained just after the release.
View SolutionDraw a line segment AB of length 8cm. At each end of this line segment, draw a line perpendicular to AB. Are these two lines parallel?
View SolutionTwo identical balls , each having a charge q and mass m , are suspended from a common point by two insultating strings each of length L. The balls are held at a separation x and then released. Find
(a) the electric force on each ball
(b) the component of the resultant force on a ball along and perpendicular to string
(c ) the tension in the string
(d) the acceleration of one of the balls. Consider the situation only for the instant just after the release.
View SolutionTwo light strings of length 4 cm and 3 cm are tied to a bob of weight 500 gm. The free ends of the strings are tied to pegs in the same horizontal line and separated by 5 cm. The ratio of tension in the longer string to that in the shorter string is
View SolutionTwo particle of masses 10 kg and 35 kg are connected with four strings at points B and D as shown in fig.

Determine the tension in various segments of the string.
View Solution
