Two indentical balls, each having a charge of 2.00×10−7C and a mass of 100g , are suspended from a common point by two insulating strings each 50 cm long. The balls are held at a separation 5.0cm apart and then released. Find (a) the electric force on one of the charged balls (b) the components of the resultant force on it alongand perpendicular to the string (c) the tension is the string (d) the components of the resultant force on it along and perpendicular to the string(c) the tension in the string (d) the acceleration of one of the balls. Answers are to be obtained just after the release.
Q1=Q2=2×10−7C,
M=100gm
l=50cm=50×10−2m,
D=5×10−2m
(a) Now electric force
F=KQ1Q2D2
=14.4N×10−2N=0.144N
(b) The components of resultant force along it is Z,because mg balances T costheta.
also,F=mg=Tsinθ
(c)Tansionofthestr∈g
Tsinθ=F
Tcosθ=mg
T2=F2+(mg)2
=(0.144)2+(0.1×9.8)2
i.e.T=0.986N.
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 2
8 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMACHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Exercises
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
Similar Questions
Two identical balls , each having a charge q and mass m , are suspended from a common point by two insultating strings each of length L. The balls are held at a separation x and then released. Find
(a) the electric force on each ball
(b) the component of the resultant force on a ball along and perpendicular to string
(c ) the tension in the string
(d) the acceleration of one of the balls. Consider the situation only for the instant just after the release.
View SolutionTwo small spheres, each having a mass of 20 g, are suspended form a common point by two insulating strings of length 40 cm each. The spheres are identically charged and the speration between the balls at equilibrium is found to be 4 cm . Find the charge on each sphere.
View Solution
Knowledge Check
Two path balls carrying eqaul chareges are suspended froom a common point by strings of equal length, the strings are rightly clamped at half the height. The equilibrium separation between the balls, now becomes :
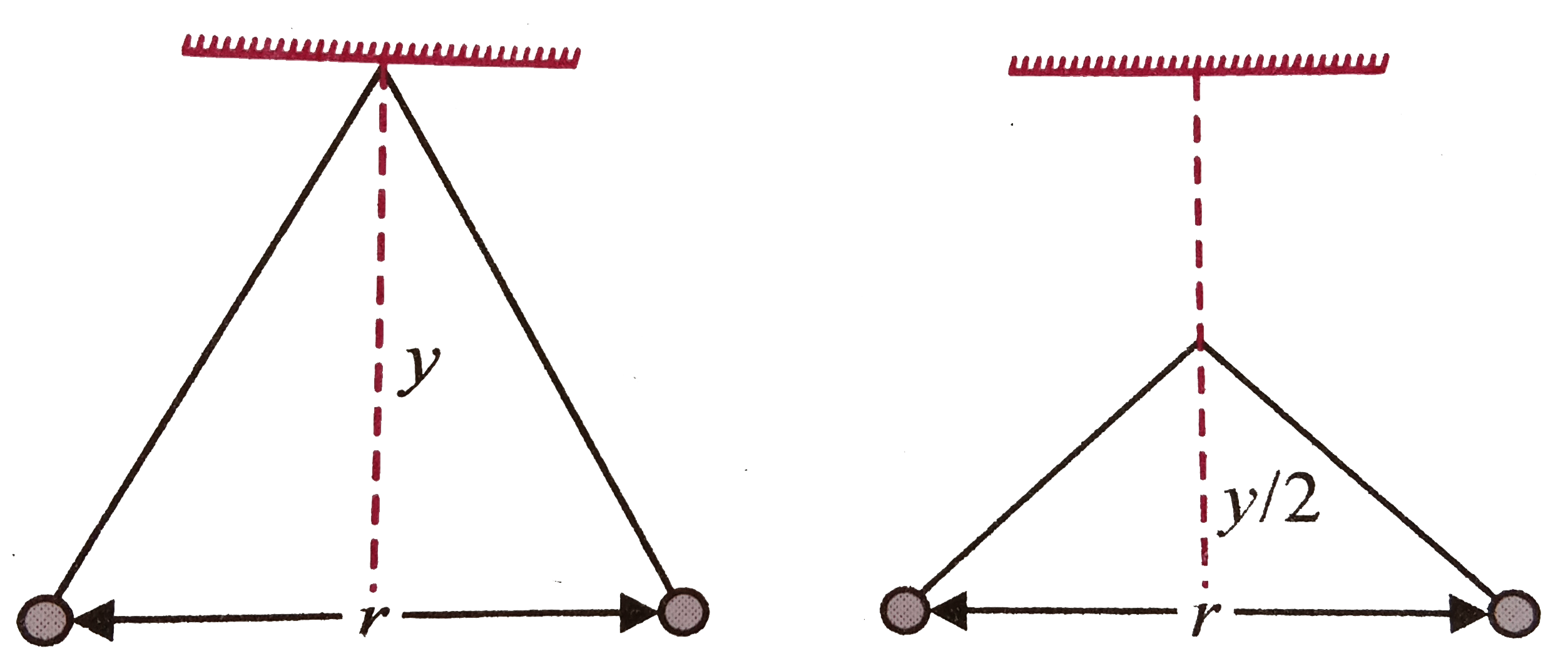 A(2r3)B(1√2)2C(r3√2)D(2r√3)
A(2r3)B(1√2)2C(r3√2)D(2r√3)Two identical tennis balls each having mass 'm' and charge 'q' are suspended from a fixed point by threads of length 'l'. What is the equilibrium separation when each thread makes a small angle 'θ' with the vertical ?
Ax=(q2l2πε0mg)1/2Bx=(q2l2πε0mg)1/3Cx=(q2l22πε0m2g)1/3Dx=(q2l22πε0m2g2)1/3
Two indentical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionThree small balls, each of mass 10 g , are suspended from a common point by 1-m silk threads . The balls are identically charged and hung at the corners of an equiliteral triangle of 0.1 m. What is the charge on each ball ?
View SolutionTwo identical balls each having a density ρ are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle θ with vertical. Now, both the balls are immersed in a liquid. As a result the angle θ does not change. The density of the liquid is σ. Find the dielectric constant of the liquid.
View SolutionTwo charged particles are placed at a distance 1.0 cm apart. What is the minimum possible magnitude of the electric force acting o each charge?
View SolutionThree small balls, each of mass 10 gm are suspended separately from common point. by silk threads, each one meter long. The balls are identically charged and hang at the corners of an equilateral triangle of side 0.1. metre. Find the charge on each ball?
View SolutionTwo pith ball of mass 0.5 each are suspended from a common point O by means of silk threads, each of length 20 cm. When the balls are given equal and similar charges, they repel each other so that the two threads make an angle of 60∘ with each-other. Determine the charge on each ball.
View Solution
