A ball is dropped from a building of height 45 m. Simultaneously another ball is thrown up with a speed 40 m/s. The relative speed of the balls varies with time as
t0
t1
t2
1t
The correct Answer is:A
To solve the problem of the relative speed of two balls—one dropped from a height and the other thrown upwards—we can follow these steps:
Step 1: Identify the initial conditions of both balls.
- Ball A (dropped from a height of 45 m):
- Initial velocity (u_A) = 0 m/s (since it is dropped)
- Acceleration (a_A) = g = 9.81 m/s² (downward)
- Ball B (thrown upwards):
- Initial velocity (u_B) = 40 m/s (upward)
- Acceleration (a_B) = -g = -9.81 m/s² (since it is moving against gravity)
Step 2: Write the equations of motion for both balls.
- For Ball A (dropped):
hA(t)=h0−12gt2
where h0=45 m is the initial height.
- For Ball B (thrown upwards):
hB(t)=uBt−12gt2
where uB=40 m/s.
Step 3: Determine the relative speed of the balls.
The relative speed of two objects is given by the difference in their velocities. The velocity of each ball can be derived from their equations of motion.
- Velocity of Ball A (v_A):
vA(t)=0+gt=gt
- Velocity of Ball B (v_B):
vB(t)=uB−gt=40−gt
Now, the relative velocity (v_rel) of Ball A with respect to Ball B is:
vrel(t)=vA(t)−vB(t)=(gt)−(40−gt)=2gt−40
Step 4: Substitute the value of g.
Using g=9.81 m/s²:
vrel(t)=2(9.81)t−40=19.62t−40
Conclusion:
The relative speed of the balls varies linearly with time and is given by:
vrel(t)=19.62t−40 m/s
- Ball A (dropped from a height of 45 m):
- Initial velocity (u_A) = 0 m/s (since it is dropped)
- Acceleration (a_A) = g = 9.81 m/s² (downward)
- Initial velocity (u_B) = 40 m/s (upward)
- Acceleration (a_B) = -g = -9.81 m/s² (since it is moving against gravity)
- For Ball A (dropped):
hA(t)=h0−12gt2
where h0=45 m is the initial height.
hB(t)=uBt−12gt2
where uB=40 m/s.
The relative speed of two objects is given by the difference in their velocities. The velocity of each ball can be derived from their equations of motion.
vA(t)=0+gt=gt
vB(t)=uB−gt=40−gt
vrel(t)=vA(t)−vB(t)=(gt)−(40−gt)=2gt−40
Using g=9.81 m/s²:
vrel(t)=2(9.81)t−40=19.62t−40
The relative speed of the balls varies linearly with time and is given by:
vrel(t)=19.62t−40 m/s
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - PRACTICE EXERCISE
58 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - problems
47 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - EXERCISE -I
58 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III
49 Videos
Similar Questions
A ball A is dropped from a building of height 45m. Simultaneously another ball B is thrown up with a speed 40m/s. Calculate the relative speed of the balls as a function of time.
View SolutionA ball is dropped from the top of a building of height 80 m. At same instant another ball is thrown upwards with speed 50 m/s from the bottom of the building. The time at which balls will meet is
View Solution
Knowledge Check
A ball A is dropped from a building of height 45m. Simultaneously another ball B is thrown up with a speed 40m/s. Calculate the relative speed of the balls as a function of time.
A0B10ms−1C25ms−1D50ms−1
A ball is throuwn with a speed of 20 m//s from top of a buling 150 m high and simultaneously another ball is thrown vertically upward witn a speed of 30 m/s from the foot of the builing . Find the time when both the balls will meet (g=10m/s2)
View SolutionA ball is thrown downwards with a speed of 20ms−1, from the top of a building 150m high and simultaneously another ball is thrown vertically upwards with a speed of 30ms−1 from the foot to the building . Find the time after which both the balls will meet. (g=10 m s^(-2))
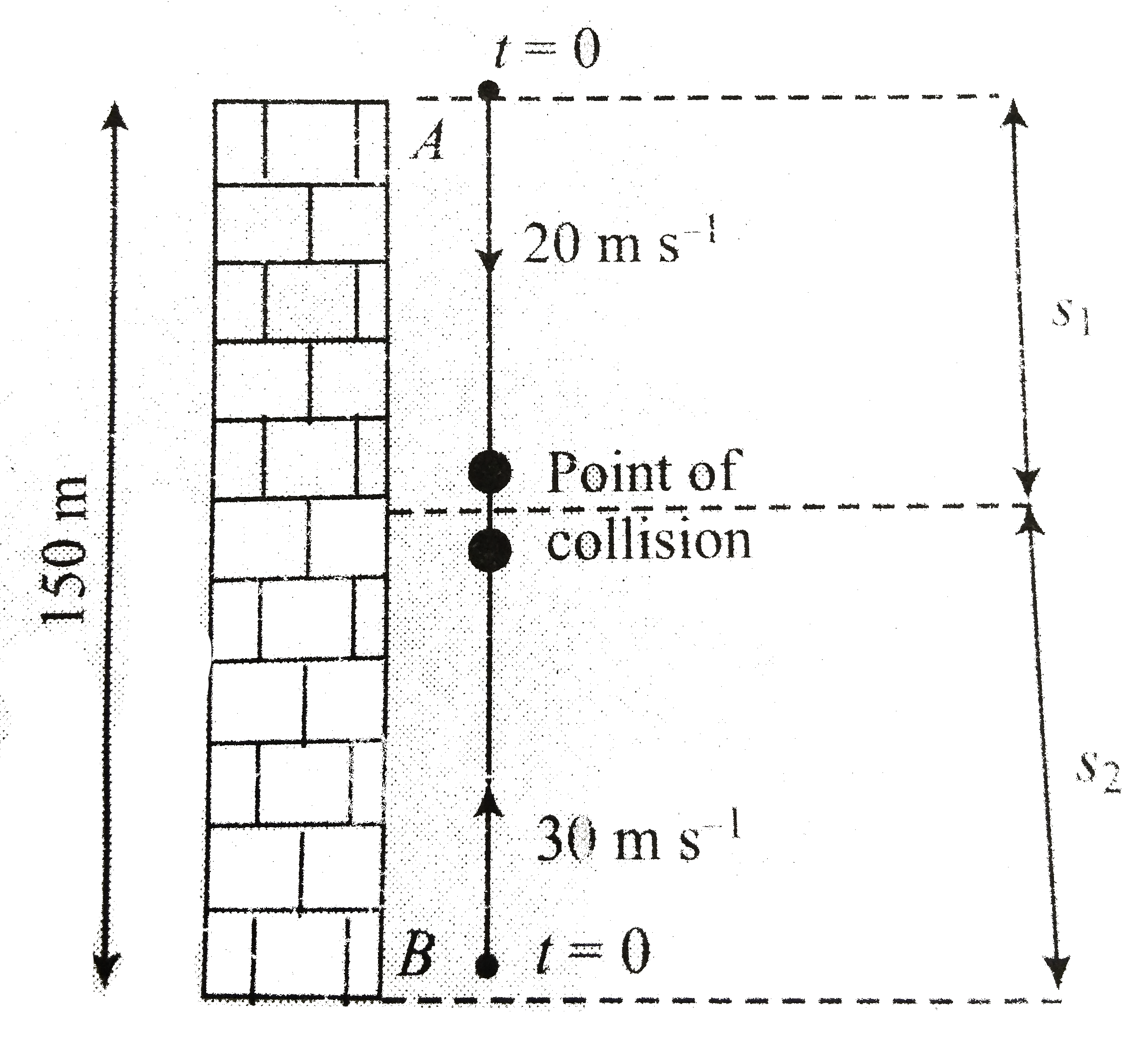 .
.
View SolutionA ball is dropped from the top of a building 100 m high. At the same instant another ball is thrown upwards with a velocity of 40ms−1 from the bottom of the building. The two balls will meet after.
View SolutionA ball is dropped from the top of a building 100 m high. At the same instant another ball is thrown upwards with a velocity of 40ms−1 from the bottom of the building. The two balls will meet after.
View SolutionA ball is dropped from the top of a tower of height 78.4 m Another ball is thrown down with a certain velocity 2 sec later. If both the balls reach the ground simultaneously, the velocity of the second ball is
View SolutionA ball is thrown up at a speed of 4.0 m/s. Find the maximum height reached by the ball. Take g=10m/s2.
View SolutionA ball is dropped from top of a tower 250 m high. At the same time, another ball is thrown upwards with a velocity of 50ms−1 from the ground. The time at which they cross each other is
View Solution
