A ball is dropped from a height of 19.6 m above the ground. It rebounds from the ground and raises itself up to the same height. Take the starting point as the origin and vertically downward as the positive X-axis. Draw approximate plots of x versus t, v versus t and a versus t. Neglect the small interval during which the ball was in contact with the ground.
To solve the problem, we will analyze the motion of the ball in two parts: the downward motion (from height to the ground) and the upward motion (from the ground back to the height). We will also derive the necessary equations and sketch the graphs for displacement, velocity, and acceleration.
Step 1: Analyze the downward motion
1. Initial Conditions:
- Initial height (h) = 19.6 m
- Initial velocity (u) = 0 m/s (the ball is dropped)
- Acceleration (a) = 9.8 m/s² (due to gravity, acting downward)
2. Using the equation of motion:
The displacement (s) can be calculated using the equation:
s=ut+12at2
Here, s=19.6 m, u=0, and a=9.8 m/s².
19.6=0+12×9.8×t2
Simplifying gives:
19.6=4.9t2⟹t2=19.64.9=4⟹t=2 seconds
Step 2: Analyze the upward motion
1. Initial Conditions:
- At the ground (point B), the ball rebounds with the same speed it hit the ground, which is v=19.6 m/s (downward).
- Initial velocity (u) for the upward motion = -19.6 m/s (upward direction is negative in our convention).
- Acceleration (a) = -9.8 m/s² (acting downward).
2. Using the same equation of motion:
The time taken to reach the height again can be calculated using:
s=ut+12at2
Here, s=19.6 m, u=−19.6 m/s, and a=−9.8 m/s².
19.6=−19.6t+12(−9.8)t2
Rearranging gives:
0=−4.9t2−19.6t+19.6
This is a quadratic equation in the form at2+bt+c=0. Solving this will yield the time taken for the upward motion, which will also be 2 seconds.
Step 3: Total time of motion
The total time for the entire motion (down and up) is:
Total time=2 seconds (down)+2 seconds (up)=4 seconds
Step 4: Draw the graphs
1. Displacement vs. Time (x vs. t):
- At t=0, x=0 m.
- At t=2 s, x=19.6 m (maximum height).
- At t=4 s, x=0 m (back to the ground).
- The graph is a parabola opening upwards from (0,0) to (2, 19.6) and back to (4,0).
2. Velocity vs. Time (v vs. t):
- At t=0, v=0 m/s.
- At t=2 s, v=19.6 m/s (just before hitting the ground).
- Instantaneously after hitting the ground, v becomes -19.6 m/s (upward).
- At t=4 s, v=0 m/s (at maximum height).
- The graph is a linear line increasing from (0,0) to (2,19.6) and then decreasing from (2,-19.6) to (4,0).
3. Acceleration vs. Time (a vs. t):
- The acceleration is constant at 9.8 m/s² for the downward motion and remains constant at −9.8 m/s² for the upward motion.
- The graph will show a constant value of 9.8 m/s² from t=0 to t=2 seconds, a discontinuity at t=2 seconds, and then a constant value of −9.8 m/s² from t=2 to t=4 seconds.
Summary of Graphs:
- Displacement vs. Time: Parabolic shape, starting at (0,0), peaking at (2,19.6), and returning to (4,0).
- Velocity vs. Time: Linear increase to (2,19.6), instantaneous drop to (-19.6) at t=2, then linear decrease to (4,0).
- Acceleration vs. Time: Constant 9.8 m/s² from t=0 to t=2, discontinuity at t=2, then constant −9.8 m/s² from t=2 to t=4.
- Initial height (h) = 19.6 m
- Initial velocity (u) = 0 m/s (the ball is dropped)
- Acceleration (a) = 9.8 m/s² (due to gravity, acting downward)
The displacement (s) can be calculated using the equation:
s=ut+12at2
Here, s=19.6 m, u=0, and a=9.8 m/s².
19.6=0+12×9.8×t2
Simplifying gives:
19.6=4.9t2⟹t2=19.64.9=4⟹t=2 seconds
- At the ground (point B), the ball rebounds with the same speed it hit the ground, which is v=19.6 m/s (downward).
- Initial velocity (u) for the upward motion = -19.6 m/s (upward direction is negative in our convention).
- Acceleration (a) = -9.8 m/s² (acting downward).
The time taken to reach the height again can be calculated using:
s=ut+12at2
Here, s=19.6 m, u=−19.6 m/s, and a=−9.8 m/s².
19.6=−19.6t+12(−9.8)t2
Rearranging gives:
0=−4.9t2−19.6t+19.6
This is a quadratic equation in the form at2+bt+c=0. Solving this will yield the time taken for the upward motion, which will also be 2 seconds.
Total time=2 seconds (down)+2 seconds (up)=4 seconds
- At t=0, x=0 m.
- At t=2 s, x=19.6 m (maximum height).
- At t=4 s, x=0 m (back to the ground).
- The graph is a parabola opening upwards from (0,0) to (2, 19.6) and back to (4,0).
- At t=0, v=0 m/s.
- At t=2 s, v=19.6 m/s (just before hitting the ground).
- Instantaneously after hitting the ground, v becomes -19.6 m/s (upward).
- At t=4 s, v=0 m/s (at maximum height).
- The graph is a linear line increasing from (0,0) to (2,19.6) and then decreasing from (2,-19.6) to (4,0).
- The acceleration is constant at 9.8 m/s² for the downward motion and remains constant at −9.8 m/s² for the upward motion.
- The graph will show a constant value of 9.8 m/s² from t=0 to t=2 seconds, a discontinuity at t=2 seconds, and then a constant value of −9.8 m/s² from t=2 to t=4 seconds.
- Displacement vs. Time: Parabolic shape, starting at (0,0), peaking at (2,19.6), and returning to (4,0).
- Velocity vs. Time: Linear increase to (2,19.6), instantaneous drop to (-19.6) at t=2, then linear decrease to (4,0).
- Acceleration vs. Time: Constant 9.8 m/s² from t=0 to t=2, discontinuity at t=2, then constant −9.8 m/s² from t=2 to t=4.
Topper's Solved these Questions
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective -1
13 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective -2
9 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer
14 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
Similar Questions
A ball is dropped from a height h above ground. Neglect the air resistance, its velocity (v) varies with its height (y) above the ground as :-
View SolutionA ball is dropped from a height of 320m above the ground. After every collision, the speed of ball decreases by 50%. Taking dropping point as origin, downward direction positive and collision time negligible, sketch the v-t, s-t and a-t graphs. Also calculate the total distance traveled by the ball and the total time of journey.
View Solution
Knowledge Check
A ball is dropped from a height h on the ground If the coefficient of restitution is e, the height to which the ball goes up after it rebounds for the nth time is
Ahe2nBhenCe2nhDhe2nA ball is dropped vertically from a height d above the ground. It hits the ground and bounces up vertically to a height d/2. Neglecting subsequent motion and air resistance, its velocity v varies with the heiht h above the ground as
A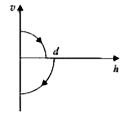 B
B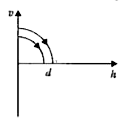 C
C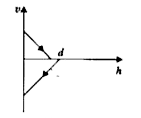 D
D
A ball is released from the top of a tower of height h metre. It takes T second to reach the ground. What is the position of the ball in T3 second?
View SolutionA ball is released from the top of a tower of height h metre. It takes T second to reach the ground. What is the position of the ball in T3 second?
View SolutionA ball is released from the top of a tower of height h metre. It takes T second to reach the ground. What is the position of the ball in T3 second?
View SolutionA ball is released from the top of a tower of height h metre. It takes T second to reach the ground. What is the position of the ball in T3 second?
View SolutionA ball of mass 50 g is dropped from a height of 20 m. A boy on the ground hits the ball vertically upwards with a bat with an average force of 200 N, so that it attains a vertical height of 45 m. The time for which the ball remains in contact with the bat is [Take g=10m/s2]
View SolutionA ball is dropped from height 5m. The time after which ball stops rebounding if coefficient of restitution between ball and ground e=1/2, is
View Solution
