A ball is dropped vertically from a height d above the ground . It hits the ground and bounces up vertically to a height (d)/(2).Neg≤ct∈g⊂sequentmotionandairresistance,itsvelocityvvarieswiththeheighth above the ground as

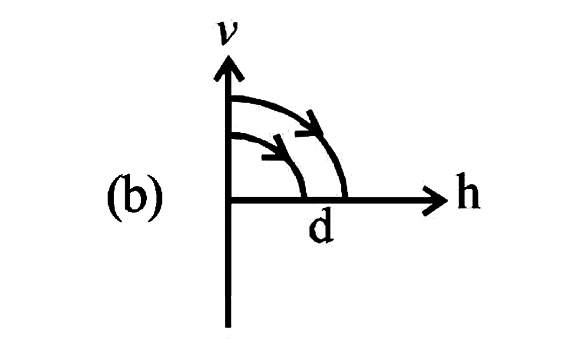
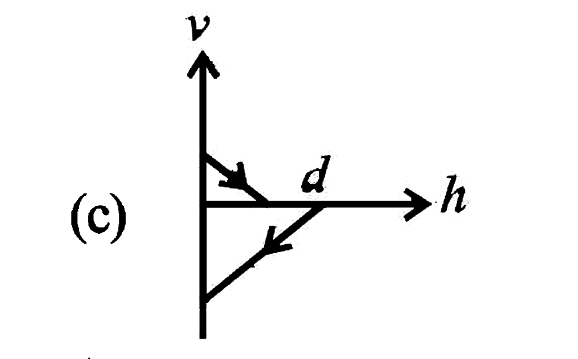
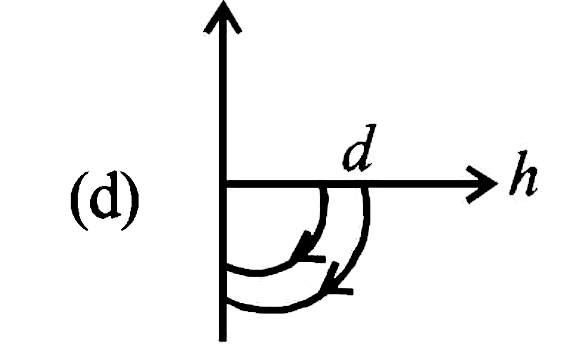
The correct Answer is:A
To solve the problem of how the velocity v of a ball varies with the height h above the ground after being dropped from a height d and bouncing back to a height of d2, we can follow these steps:
Step 1: Analyze the motion of the ball when dropped
When the ball is dropped from height d, it starts from rest, so its initial velocity u=0. As it falls, it accelerates due to gravity, g.
Using the equation of motion:
v2=u2+2gh
where h is the height fallen (which will be d when it hits the ground), we can find the velocity just before it hits the ground.
Substituting u=0 and h=d:
v2=0+2gd⟹v=√2gd
Step 2: Analyze the motion of the ball after bouncing
After hitting the ground, the ball bounces back to a height of d2. At the maximum height of the bounce, the final velocity v=0 and the initial velocity u can be found using the same equation of motion.
Using the equation:
v2=u2+2gh
where h=d2, we set v=0:
0=u2−2g(d2)⟹u2=gd⟹u=√gd
Step 3: Establish the relationship between velocity and height
Now we have two key points:
1. Just before hitting the ground (at height h=0), the velocity is v=√2gd.
2. At the maximum height after bouncing (at height h=d2), the velocity is v=0.
Step 4: Determine the graph of velocity vs. height
- As the ball falls from height d to height 0, the velocity increases from 0 to √2gd.
- As the ball bounces back from height 0 to height d2, the velocity decreases from √2gd to 0.
Step 5: Graphical representation
The graph of velocity v versus height h will show:
- A curve starting from (d,0) and moving to (0,√2gd) as the ball falls.
- Then it will curve back from (0,√2gd) to (d2,0) as the ball bounces back.
Conclusion
The velocity v varies with height h in a parabolic manner, reflecting the changes in kinetic and potential energy during the fall and bounce.
When the ball is dropped from height d, it starts from rest, so its initial velocity u=0. As it falls, it accelerates due to gravity, g.
v2=u2+2gh
where h is the height fallen (which will be d when it hits the ground), we can find the velocity just before it hits the ground.
v2=0+2gd⟹v=√2gd
After hitting the ground, the ball bounces back to a height of d2. At the maximum height of the bounce, the final velocity v=0 and the initial velocity u can be found using the same equation of motion.
v2=u2+2gh
where h=d2, we set v=0:
0=u2−2g(d2)⟹u2=gd⟹u=√gd
Now we have two key points:
1. Just before hitting the ground (at height h=0), the velocity is v=√2gd.
2. At the maximum height after bouncing (at height h=d2), the velocity is v=0.
- As the ball falls from height d to height 0, the velocity increases from 0 to √2gd.
- As the ball bounces back from height 0 to height d2, the velocity decreases from √2gd to 0.
The graph of velocity v versus height h will show:
- A curve starting from (d,0) and moving to (0,√2gd) as the ball falls.
- Then it will curve back from (0,√2gd) to (d2,0) as the ball bounces back.
The velocity v varies with height h in a parabolic manner, reflecting the changes in kinetic and potential energy during the fall and bounce.
Topper's Solved these Questions
Similar Questions
A ball is dropped vertically from a height d above the ground. It hits the ground and bounces up vertically to a height d/2. Neglecting the subsequent motion and the air resistance, how its velocity v varies with the height h above the ground?
View SolutionA ball is dropped vertically from a height d above the ground. It hits the ground and bounes up vertically to a height d/2. Neglecting subsequent motion and air resistance, its speed v varies with the height h above the ground as
View Solution
Knowledge Check
v34
A B
B C
C D
D
A ball is dropped from a height h above ground. Neglect the air resistance, its velocity (v) varies with its height (y) above the ground as :-
A√2g(h−y)B√2ghC√2gyD√2g(h+y)A ball is dropped from a height h on to a floor . If the cofficient of restitution is e, calculate the height the ball first rebounds ?
Ae2hBe√hCehD√eh
A ball is dropped from a height h above ground,Neglect the air resistance,its velocity (v) varies with its height y above the ground as
View SolutionA ball is dropped from a height H above the ground. It hits the ground and bounces up vertically to a height H2 where it is caught. Taking origin at the point from where the ball was dropped, plot the variation of its displacement vs velocity. Take vertically downward direction as positive.
View SolutionA ball is dropped from a height 64 m above the ground and every time it hits the ground it rises to a height equal to half of the previous height. The height attained after it hits the ground for the 16h time is
View SolutionA ball is thrown upwards with a speed u from a height h above the ground.The time taken by the ball to hit the ground is
View SolutionA body is thrown vertically upward from a point A 125 m above the ground. It goes up to a maximum height of 250 m above the ground and passes through A on its downward journey. The velocity of the body when it is at a height of 70 m above the ground is (g=10m/s2)
View Solution
