A ball is projected form a point A on a smooth inclined plane which makes an angle a to the horizontal. The velocity of projection makes an angle θ with the plane upwards. If on the second bounce the ball is moving perpendicular to the plane, find e in terms of α and θ. Here e is the coefficient of restitution between the ball and the plane.
The correct Answer is:θ−1
To solve the problem step by step, we need to analyze the motion of the ball on the inclined plane, taking into account the angles and the coefficient of restitution.
Step 1: Understanding the Projection
The ball is projected from point A on a smooth inclined plane at an angle α to the horizontal. The velocity of projection makes an angle θ with the plane upwards.
Step 2: Components of Initial Velocity
Let the initial velocity of projection be u. The components of the initial velocity can be expressed as:
- The component along the incline (x-direction):
ux=ucosθ
- The component perpendicular to the incline (y-direction):
uy=usinθ
Step 3: Time of Flight to the First Bounce
The time taken for the ball to reach the first bounce (point B) can be calculated using the vertical motion equations. The effective acceleration acting on the ball in the direction perpendicular to the incline is gcosα. The time of flight T1 can be calculated as:
T1=2uygcosα=2usinθgcosα
Step 4: Velocity Just Before the Second Bounce
When the ball strikes the inclined plane for the second time, its velocity will change due to the coefficient of restitution e. The velocity just before the second bounce can be expressed as:
v=2eusinθ
This is because the velocity component perpendicular to the incline will be reduced by the coefficient of restitution.
Step 5: Time of Flight After the First Bounce
After the first bounce, the ball will again travel upwards and then downwards. The time of flight T2 for this motion can be calculated similarly:
T2=2(2eusinθ)gcosα=4eusinθgcosα
Step 6: Total Time of Flight
The total time of flight from point A to point C (after the second bounce) is:
Ttotal=T1+T2=2usinθgcosα+4eusinθgcosα
This simplifies to:
Ttotal=2usinθ(1+2e)gcosα
Step 7: Condition for Perpendicular Motion
At the second bounce, the ball is moving perpendicular to the inclined plane, which means the horizontal component of the velocity must be zero. The horizontal component of the velocity after the first bounce can be expressed as:
ux−gsinα⋅Ttotal=0
Substituting ux=ucosθ and Ttotal:
ucosθ−gsinα⋅2usinθ(1+2e)gcosα=0
Step 8: Solving for Coefficient of Restitution e
From the equation above, we can simplify and solve for e:
ucosθ=2usinθ(1+2e)sinαcosα
Dividing through by u and rearranging gives:
cosθ=2sinθtanα(1+2e)
Solving for e:
1+2e=cosθ2sinθtanα
2e=cosθ2sinθtanα−1
e=12(cosθ2sinθtanα−1)
Final Expression for Coefficient of Restitution
Thus, the coefficient of restitution e in terms of α and θ is:
e=12(cosθ2sinθtanα−1)
The ball is projected from point A on a smooth inclined plane at an angle α to the horizontal. The velocity of projection makes an angle θ with the plane upwards.
Let the initial velocity of projection be u. The components of the initial velocity can be expressed as:
- The component along the incline (x-direction):
ux=ucosθ
- The component perpendicular to the incline (y-direction):
uy=usinθ
The time taken for the ball to reach the first bounce (point B) can be calculated using the vertical motion equations. The effective acceleration acting on the ball in the direction perpendicular to the incline is gcosα. The time of flight T1 can be calculated as:
T1=2uygcosα=2usinθgcosα
When the ball strikes the inclined plane for the second time, its velocity will change due to the coefficient of restitution e. The velocity just before the second bounce can be expressed as:
v=2eusinθ
This is because the velocity component perpendicular to the incline will be reduced by the coefficient of restitution.
After the first bounce, the ball will again travel upwards and then downwards. The time of flight T2 for this motion can be calculated similarly:
T2=2(2eusinθ)gcosα=4eusinθgcosα
The total time of flight from point A to point C (after the second bounce) is:
Ttotal=T1+T2=2usinθgcosα+4eusinθgcosα
This simplifies to:
Ttotal=2usinθ(1+2e)gcosα
At the second bounce, the ball is moving perpendicular to the inclined plane, which means the horizontal component of the velocity must be zero. The horizontal component of the velocity after the first bounce can be expressed as:
ux−gsinα⋅Ttotal=0
Substituting ux=ucosθ and Ttotal:
ucosθ−gsinα⋅2usinθ(1+2e)gcosα=0
From the equation above, we can simplify and solve for e:
ucosθ=2usinθ(1+2e)sinαcosα
Dividing through by u and rearranging gives:
cosθ=2sinθtanα(1+2e)
Solving for e:
1+2e=cosθ2sinθtanα
2e=cosθ2sinθtanα−1
e=12(cosθ2sinθtanα−1)
Thus, the coefficient of restitution e in terms of α and θ is:
e=12(cosθ2sinθtanα−1)
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Single Correct
141 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.3
24 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A ball is projected from a point in a horizontal plane with a velocity of 20 m/s at 30∘ with the horizontal. Coefficient of restitution is 0.8, then
View SolutionA block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
View SolutionA block is placed on a smooth inclined plane at an angle 'θ' to the horizontal. The acceleration must the plane be moved horizontally so that the block to fall freely is
View SolutionA projectile is fired with a velocity v at right angle to the slope inclined at an angle θ with the horizontal. The range of the projectile along the inclined plane is
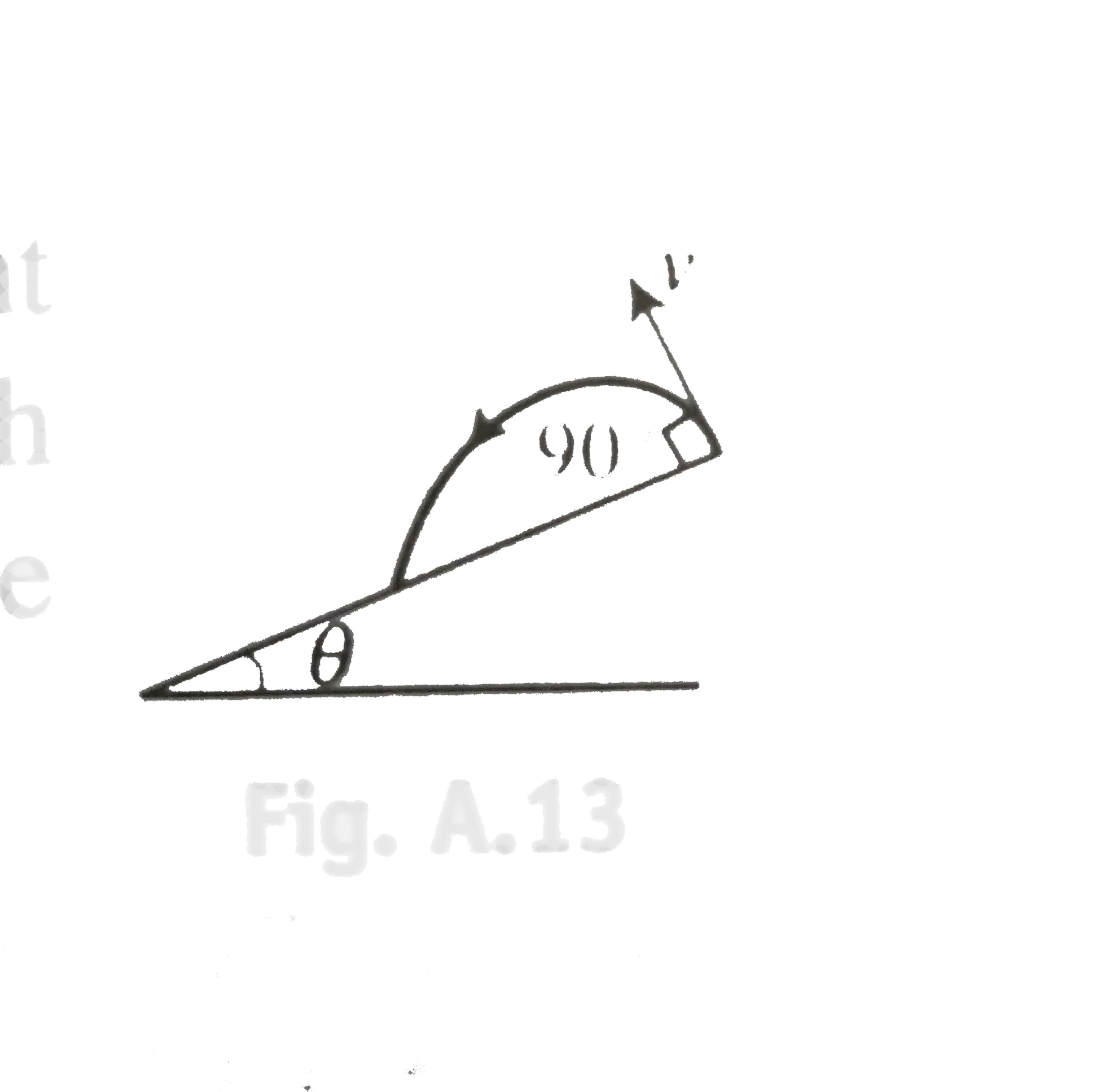
View SolutionA ball is projected horizontally with a speed v from the top of the plane inclined at an angle 45∘ with the horizontal. How far from the point of projection will the ball strikes the plane?
View SolutionA block slides down an inclined plane that makes an angle θ with the horizontal. If the coefficient of kinetic friction is μ, find the acceleration of the block.
View Solution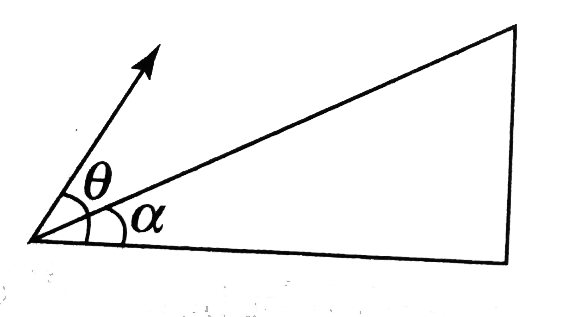
A projectile is fired at an angle θ with the horizontal. Find the condition under which it lands perpendicular on an inclined plane inclination α as shown figure.
View SolutionA block is lying on an inclined plane which makes an angle of 60∘ with the horizontal. If coefficient of friction between the block and the plane is 0.25 and g = 10 ms−2, the acceleration of block when it is moves along the plane will be
View SolutionA ball falls freely form a height onto and smooth inclined plane forming an angle a with the horizontal. Find the ratio of the distance between the points at which the jumping ball strikes the inclined plane. Assume the impacts to be elastic.
View SolutionA particle is projected with a velocity u making an angle θ with the horizontal. The instantaneous power of the gravitational force
View Solution
