A block is placed on a smooth inclined plane at an angle 'θ' to the horizontal. The acceleration must the plane be moved horizontally so that the block to fall freely is
gtanq
gcotq
gsinq
gcosq
The correct Answer is:B
To solve the problem of determining the acceleration that the inclined plane must have in order for the block to fall freely, we can follow these steps:
1. Understanding the Forces:
- The block experiences gravitational force acting downward, which is equal to mg, where m is the mass of the block and g is the acceleration due to gravity.
- The inclined plane is at an angle θ to the horizontal.
2. Condition for Free Fall:
- For the block to fall freely, the normal force N between the block and the inclined plane must be zero. This means that the only force acting on the block in the vertical direction is its weight.
3. Setting Up the Equations:
- When the inclined plane accelerates horizontally with acceleration a, we can analyze the forces acting on the block.
- The component of the gravitational force acting down the incline is mgsinθ.
- The component of the gravitational force acting perpendicular to the incline is mgcosθ.
4. Applying Newton's Second Law:
- In the direction perpendicular to the incline, the block is in equilibrium when the normal force is zero:
N−mgcosθ=0⇒N=mgcosθ
- Since N=0 for free fall, we have:
0=mgcosθ
5. Analyzing the Incline's Acceleration:
- The block will also experience a pseudo force due to the acceleration of the inclined plane. This pseudo force acts horizontally opposite to the direction of the incline’s acceleration.
- The effective force acting on the block along the incline due to this pseudo force is masinθ.
- For the block to fall freely, the net force along the incline must equal the gravitational force component down the incline:
masinθ=mgcosθ
6. Solving for Acceleration a:
- Dividing both sides by m (assuming m≠0):
asinθ=gcosθ
- Rearranging gives:
a=gcosθsinθ
- This simplifies to:
a=gcotθ
Final Answer:
The acceleration that the inclined plane must have for the block to fall freely is:
a=gcotθ
- The block experiences gravitational force acting downward, which is equal to mg, where m is the mass of the block and g is the acceleration due to gravity.
- The inclined plane is at an angle θ to the horizontal.
- For the block to fall freely, the normal force N between the block and the inclined plane must be zero. This means that the only force acting on the block in the vertical direction is its weight.
- When the inclined plane accelerates horizontally with acceleration a, we can analyze the forces acting on the block.
- The component of the gravitational force acting down the incline is mgsinθ.
- The component of the gravitational force acting perpendicular to the incline is mgcosθ.
- In the direction perpendicular to the incline, the block is in equilibrium when the normal force is zero:
N−mgcosθ=0⇒N=mgcosθ
- Since N=0 for free fall, we have:
0=mgcosθ
- The block will also experience a pseudo force due to the acceleration of the inclined plane. This pseudo force acts horizontally opposite to the direction of the incline’s acceleration.
- The effective force acting on the block along the incline due to this pseudo force is masinθ.
- For the block to fall freely, the net force along the incline must equal the gravitational force component down the incline:
masinθ=mgcosθ
- Dividing both sides by m (assuming m≠0):
asinθ=gcosθ
- Rearranging gives:
a=gcosθsinθ
- This simplifies to:
a=gcotθ
The acceleration that the inclined plane must have for the block to fall freely is:
a=gcotθ
Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A PLANE
87 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
Similar Questions
A block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View Solution
A block is placed on a smooth wedge of inclination angle θ with the horizontal. What minimum acceleration should be given to the wedge in the horizontal direction so that the block starts moving up along the incline?
View SolutionA small block of mass m rests on a smooth wedge of angle θ. With what horizontal accelaration a should the wedge be pulled, as shown in fig, so that the block falls freely?
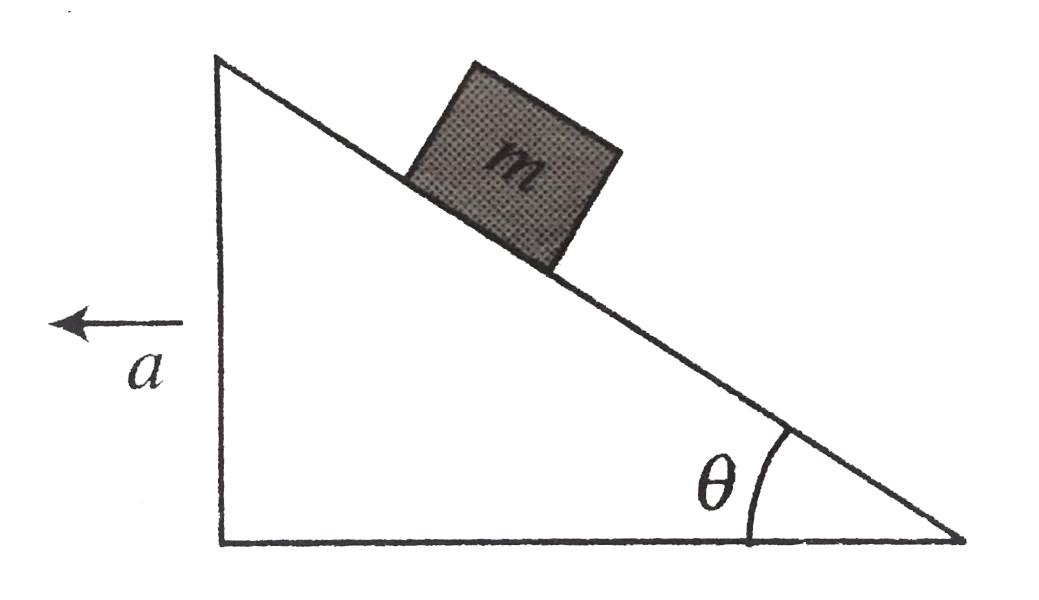
View SolutionA small block of mass m rests on a smooth wedge of angle θ. With what horizontal accelaration a should the wedge be pulled, as shown in fig, so that the block falls freely?

View SolutionA sphere is rolling down a plane of inclination θ to the horizontal. The acceleration of its centre down the plane is
View SolutionA block is placed on a smooth inclined plane as shown . For what value of horizontal force F, the block will remain at rest ?

View SolutionA body is placed on a smooth inclined plane of inclination 1 in x. The horizontal acceleration to be given to the inclined plane so that the body on it remains at rest with respect to inclined plane is
View SolutionStatement I: A block of mass m is placed on a smooth inclined plane of inclinaton θ with the horizontal. The force exerted by the plane on the block has a magnitude mgcosθ.
Statement II: Normal reaction always acts perpendicular to the contact surface.
View SolutionA block slides down an inclined plane that makes an angle θ with the horizontal. If the coefficient of kinetic friction is μ, find the acceleration of the block.
View Solution
