A ball is rolled off the edge of a horizontal table at a speed of 4m/second. It hits the ground after 0.4 second . Which statement given below is true
It hits the ground at a horizontal distance 1.6 m from the edge of the table
The speed with which it hits the ground is 4.0ms−1
Height of the table 1m
It hits the ground at an angle of 60∘ to the horizontal
The correct Answer is:A
To solve the problem step by step, we will analyze the motion of the ball as it rolls off the table. The motion can be divided into horizontal motion and vertical motion.
Step 1: Identify the Horizontal Motion
The ball rolls off the table with a horizontal speed of ux=4m/s. The time it takes to hit the ground is given as t=0.4s.
Step 2: Calculate the Horizontal Distance
To find the horizontal distance d the ball travels before hitting the ground, we can use the formula:
d=ux⋅t
Substituting the known values:
d=4m/s⋅0.4s=1.6m
Thus, the ball hits the ground at a horizontal distance of 1.6m from the edge of the table.
Step 3: Analyze the Vertical Motion
Next, we consider the vertical motion to find the height of the table. The initial vertical velocity uy=0 (since the ball rolls off horizontally), and the acceleration due to gravity a=10m/s2.
Using the equation of motion for vertical displacement:
h=uy⋅t+12at2
Substituting the known values:
h=0⋅0.4+12⋅10⋅(0.4)2
Calculating:
h=12⋅10⋅0.16=0.8m
So, the height of the table is 0.8m, which contradicts the statement that the height is 1m.
Step 4: Determine the Final Speed at Impact
To find the speed with which it hits the ground, we need to calculate the vertical component of the velocity just before impact. Using the formula:
vy=uy+a⋅t
Substituting the known values:
vy=0+10⋅0.4=4m/s
The total speed at impact can be calculated using Pythagorean theorem since the horizontal and vertical motions are independent:
v=√(ux)2+(vy)2=√(4)2+(4)2=√16+16=√32=4√2m/s
Thus, the speed with which it hits the ground is not 4m/s.
Step 5: Determine the Angle of Impact
The angle θ at which the ball hits the ground can be determined using:
tanθ=vyux=44=1
Thus, θ=45∘, which is not 60∘.
Conclusion
Based on the calculations:
1. The ball hits the ground at a horizontal distance of 1.6m from the edge of the table (True).
2. The speed with which it hits the ground is not 4m/s (False).
3. The height of the table is 0.8m (False).
4. It hits the ground at an angle of 45∘ (False).
Final Answer
The only true statement is: It hits the ground at a horizontal distance of 1.6 m from the edge of the table.
---
The ball rolls off the table with a horizontal speed of ux=4m/s. The time it takes to hit the ground is given as t=0.4s.
To find the horizontal distance d the ball travels before hitting the ground, we can use the formula:
d=ux⋅t
Substituting the known values:
d=4m/s⋅0.4s=1.6m
Thus, the ball hits the ground at a horizontal distance of 1.6m from the edge of the table.
Next, we consider the vertical motion to find the height of the table. The initial vertical velocity uy=0 (since the ball rolls off horizontally), and the acceleration due to gravity a=10m/s2.
h=uy⋅t+12at2
Substituting the known values:
h=0⋅0.4+12⋅10⋅(0.4)2
Calculating:
h=12⋅10⋅0.16=0.8m
So, the height of the table is 0.8m, which contradicts the statement that the height is 1m.
To find the speed with which it hits the ground, we need to calculate the vertical component of the velocity just before impact. Using the formula:
vy=uy+a⋅t
Substituting the known values:
vy=0+10⋅0.4=4m/s
The total speed at impact can be calculated using Pythagorean theorem since the horizontal and vertical motions are independent:
v=√(ux)2+(vy)2=√(4)2+(4)2=√16+16=√32=4√2m/s
Thus, the speed with which it hits the ground is not 4m/s.
The angle θ at which the ball hits the ground can be determined using:
tanθ=vyux=44=1
Thus, θ=45∘, which is not 60∘.
Based on the calculations:
1. The ball hits the ground at a horizontal distance of 1.6m from the edge of the table (True).
2. The speed with which it hits the ground is not 4m/s (False).
3. The height of the table is 0.8m (False).
4. It hits the ground at an angle of 45∘ (False).
The only true statement is: It hits the ground at a horizontal distance of 1.6 m from the edge of the table.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - B. Medical entrance1videos
MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrance12videos
MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - A. Taking it together1videos
MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective19videos
MEASUREMENT AND ERRORS
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery32videos
MOTION IN A PLANE
Similar Questions
A ball rolls off the edge of a horizontal table top 4 m high. If it strikes the floor at a point 5 m horizontally away from the edge of the table, what was its speed at the instant it left the table?
View SolutionA body projected up reaches a point A in its path at the end of 4th second and reaches the ground after 5 seconds from the start. The height of A above the ground is (g=10m/s2)
View Solution
Knowledge Check
- Question 1 - Select One
A ball is rolled oof along the edge of table (horizontal) with velocity 4 m/s . IT hits the ground after time 0.4 s. Which one of the following is wrong ?
Athe height of the table is 0.8 mBit hits the ground at an angle of 60∘ with the verticalCit covers a horizontal distance 1.6 m from the tableDit hits the ground with vertical velocity 4 m/s. - Question 2 - Select One
A ball is rolled off along the edge of the table (horizontal ) with velocity 4ms−1 .It hits the ground after time 0.4 s. Which one of the following statements are wrong ? ( g= 10 ms^(-2)).
AThe height of the table is 0.8 m.BIt hits the ground at angle of 60∘ with the verticalCIt covers a horizontal distance 1.6 m from the tableDIt hits the ground with vertical velocity 4ms−1
An object is thrown horizontally with an initial speed of 10m/s. How far will it drop in 4 seconds ?
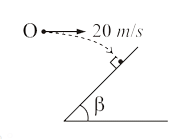
View SolutionA ball is thrown horizontally from a point O with speed 20 m/s as shown. Ball strikes the incline along normal after two seconds
The displacement of ball in two seconds will be:
 View Solution
View SolutionA ball rolls off the top of a stariway with a horizontal velocity magnitude 150 cm/sec. The steps are 20 cm high and 20 cm wide . Which step will the ball hit first ?
View SolutionA ball is thrown from a roof top at angle of 40∘above the horizontal. It hits the ground a few seconds later. At what point during its motion. Does the ball have
(a) greatest speed (b) smallest speed (c ) greatest acceleration ? Explain.View SolutionA ball is thrown horizontally from a point O with speed 20 m/s as shown. Ball strikes the incline along normal after two seconds
The speed of ball just before striking the plane is:
 View Solution
View SolutionA ball rolls off the top of a staircase with a horizontal velocity um/s. If the steps are h meter high and b meter wide, the ball will hit the edge of the nth steps, if:
View Solution
