A ball is thrown from the ground so as to just clear a wall $10 m$ high at a distance of $20 m$ and falls at a distance of $40 m$ from the wall. The magnitude and direction of the projection velocity is

A

$10 m / s, 30^{\circ}$

B

$25 m / s, 60^{\circ}$

C

$25 m / s, {tan}^{- 1} (3 / 4)$

D

$10 m / s, {tan}^{- 1} (3 / 4)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

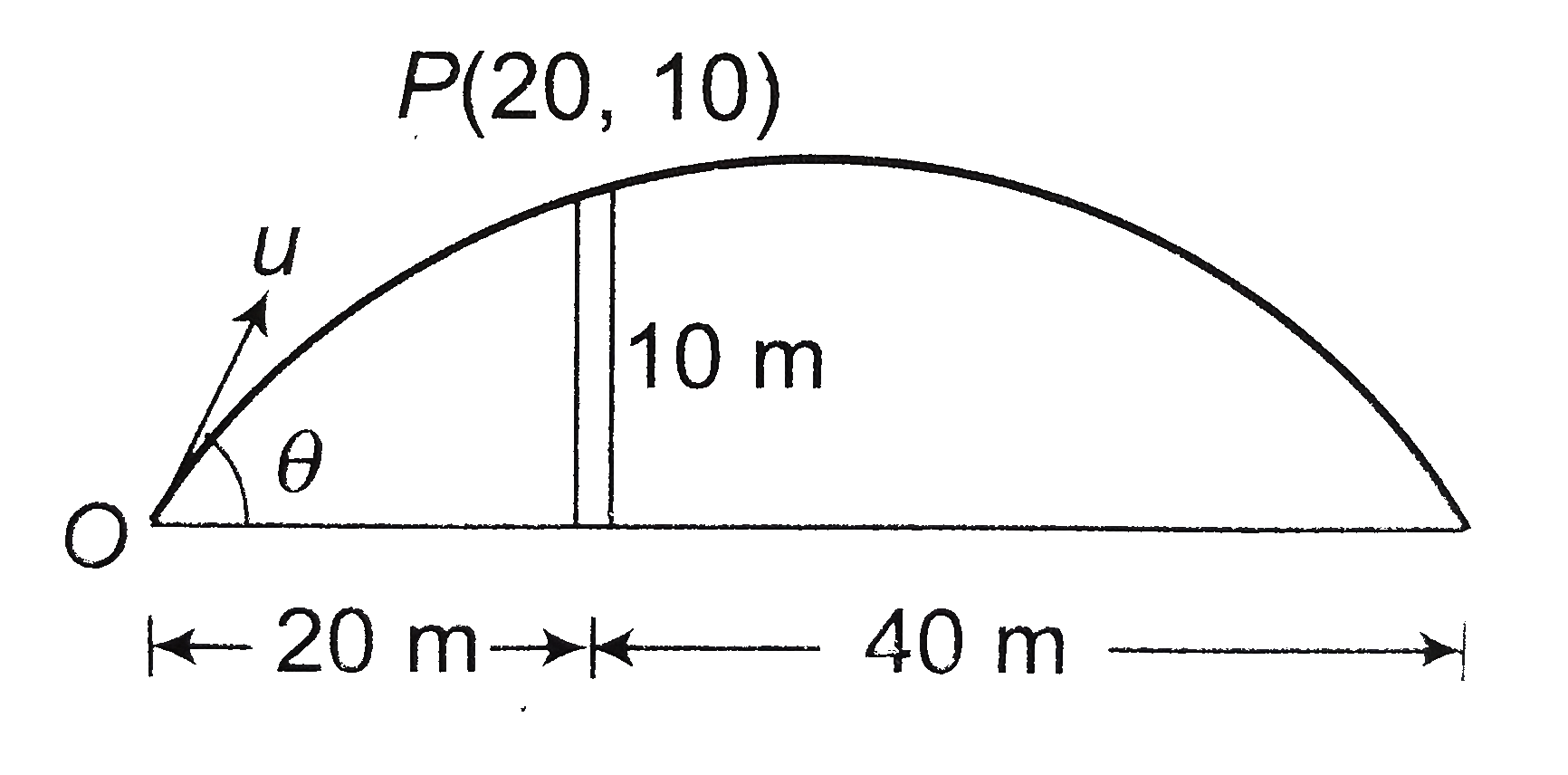
For the point $P, x = 20, y = 10$
$R = 60 m$
$y = x tan θ (1 - \frac{x}{R})$
$10 = 20 tan θ (1 - \frac{20}{60}) = \frac{40}{3} tan θ$
$tan θ = 3 / 4 \Rightarrow θ = {tan}^{- 1} (3 / 4)$

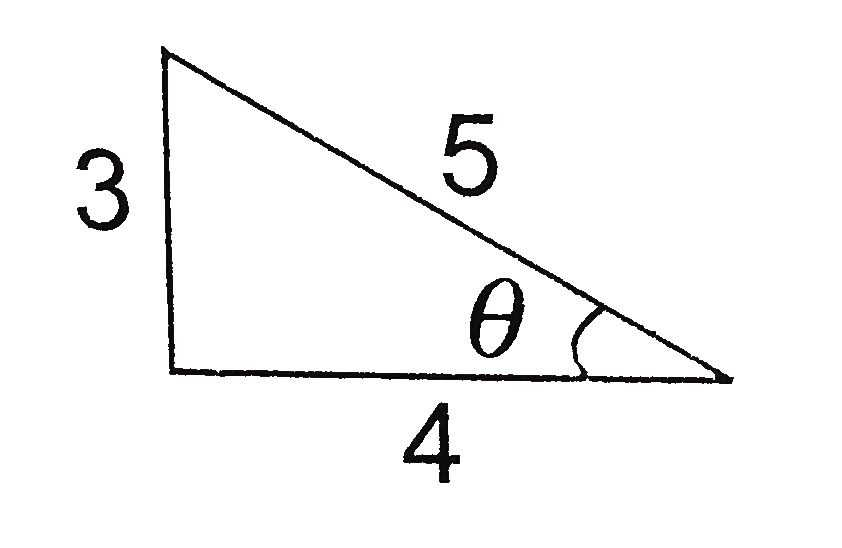
$sin θ = 3 / 5, cos θ = 4 / 5$
$R = \frac{u^{2}}{g} 2 sin θ cos θ \Rightarrow 60 = \frac{u^{2}}{10} \times 2 \times \frac{3}{5} \times \frac{4}{5}$
$u^{2} = 625 \Rightarrow u = 25 m / s$

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A ball is thrown from the ground to clear a wall 3 m high at a distance of 6 m and falls 18 m away from the wall, the angle of projection of ball is
A ${tan}^{- 1} (\frac{3}{2})$
B ${tan}^{- 1} (\frac{2}{3})$
C ${tan}^{- 1} (\frac{1}{2})$
D ${tan}^{- 1} (\frac{3}{4})$
Question 2 - Select One
A ball is thrown from the ground to clear a wall 3 m high at a distance of 6 m and falls 18 m away from the wall. Find the angle of projection of ball.
A $α = {tan}^{- 1} (\frac{1}{3})$
B $α = {tan}^{- 1} (2)$
C $α = {tan}^{- 1} (\frac{2}{3})$
D $α = {tan}^{- 1} (\frac{2}{4})$
Question 3 - Select One
A ball is thrown from the ground to clear a wall 3 m high at a distance of 6 m and falls 18 m away from the wall the angle of projection of ball is :-
A ${tan}^{- 1} (\frac{3}{2})$
B ${tan}^{- 1} (\frac{2}{3})$
C ${tan}^{- 1} (\frac{1}{2})$
D ${tan}^{- 1} (\frac{3}{4})$

CP SINGH-MOTION IN A PLANE-Exercises

Home
Ask Doubt
Profile